Skip to main content
SpringerLink
Log in

On the performance of M-QAM for Nakagami channels subject to gated noise

  • Published:
Telecommunication Systems Aims and scope Submit manuscript

Abstract

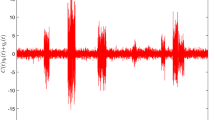
This paper presents a mathematical analysis of the joint effects of additive white Gaussian noise and gated noise in an M-ary Quadrature Amplitude Modulation communication system subject to Nakagami fading. This channel model is suitable to describe scenarios in which the Nakagami channel is affected by noisy signals originated from switching electronic circuits present in industrial environments, for example. Novel and exact analytic expressions for the bit error probability of the system are derived and computer simulations corroborate the analytic results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Lago-Fernández, J., & Salter, J. (July 2004). Modelling impulsive interference in DVB-T—Statistical analysis, test waveforms and receiver performance. Technical Report 299, BBC Research & Development.

  2. Al-Dweik, A., Hazmi, A., Sharif, B., & Tsimenidis, C. (2010). Efficient interleaving technique for OFDM system over impulsive noise channels. In Proceedings of the 21st international symposium on personal indoor and mobile radio communications (PIMRC) (pp. 167–171).

  3. Tepedelenlioğlu, C., & Gao, P. (2005). On diversity reception over fading channels with impulsive noise. IEEE Transactions on Vehicular Technology, 54(6), 2037–2047.

    Article  Google Scholar 

  4. Vempati, S. R., Pamula, V. K., Khan, H., & Tipparti, A. K. (Jan 2013). Blind multiuser detection in Nakagami-\(m\) fading channels with impulsive noise. In Proceedings of the 4th international conference on intelligent systems modelling simulation (ISMS) (pp. 519–523).

  5. Cheffena, M. (2012). Industrial wireless sensor networks: Channel modeling and performance evaluation. EURASIP Journal on Wireless Communications and Networking, 2012(1), 1–8.

    Article  Google Scholar 

  6. Madi, G., Vrigneau, B., Pousset, Y., Vauzelle, R., & Agba, B. L. (August 2010). Impulsive noise of partial discharge and its impact on minimum distance-based precoder of MIMO system. In Proceedings of the XVII European signal processing conference (pp. 1602–1606), Aalbor, Denmark.

  7. Sukanesh, R., & Sundaraguru, R. (2011). Mitigation of impulse noise in OFDM systems. Journal of Information & Computational Science, 8(12), 2403–2409.

    Google Scholar 

  8. Hikita, M., Yamashita, H., Hoshino, T., Kato, T., Hayakawa, N., Ueda, T., et al. (1998). Electromagnetic noise spectrum caused by partial discharge in air at high voltage substations. IEEE Transactions on Power Delivery, 2(13), 434–439.

    Article  Google Scholar 

  9. Yacoub, M. D. (2000). Fading distributions and co-channel interference in wireless systems. IEEE Antennas and Propagation Magazine, 42(1), 150–160.

    Article  Google Scholar 

  10. Agrawal, A., & Kshetrimayum, R. S. (2015). Analysis of UWB communication over IEEE 802.15.3a channel by superseding lognormal shadowing by mixture of Gamma distributions. AEÜ–International Journal of Electronics and Communications, 69(12), 1795–1799.

    Article  Google Scholar 

  11. He, W., Lei, H., & Pan, G. (2016). Performance modeling and analysis on conditional DF relaying scheme over Nakagami-\(m\) fading channels with integral \(m\). AEÜ—International Journal of Electronics and Communications, 70(6), 743–749.

    Article  Google Scholar 

  12. Nakagami, M. (December 1960). The \(m\)-distribution—A general formula of intensity distribution of rapid fading. In Statistical methods in radio wave propagation (pp. 3–36), Pergamon Press, Oxford.

  13. Beaulieu, N. C., & Chen, Y. (2007). A MAP estimator for the \(m\) parameter in Nakagami fading ultra-wide bandwidth indoor channels. IEEE Transactions on Wireless Communications, 6(3), 840–844.

    Article  Google Scholar 

  14. Lohan, E. S., Pajala, E., Renfors, M., Lakhzouri, A., & Laitinen, H. (September 2007). Indoor fading distributions for GPS-based pseudolite signals. In Proceedings of the international workshop on satellite and space communications (IWSSC’07) (pp. 6–10), Salzburg, Austria.

  15. Souza, R. A. A., Cogliatti, R., & Yacoub, M. D. (2014). Efficient acceptance-rejection method for Nakagami-\(m\) complex samples. IEEE Wireless Communications Letters, 3(1), 94–96.

    Article  Google Scholar 

  16. Queiroz, W. J. L., Lopes, W. T. A., Madeiro, F., & Alencar, M. S. (September 2010). An alternative method to compute the bit error probability of modulation schemes subject to Nakagami-\(m\) fading. EURASIP Journal on Advances in Signal Processing, 2010, 1–12.

  17. Ata, S. O., & Altunbas, I. (2016). Fixed-gain AF-PLNC over cascaded Nakagami-\(m\) fading channels for vehicular communications. AEÜ–International Journal of Electronics and Communications, 70(4), 510–516.

    Article  Google Scholar 

  18. Soury, H., Yilmaz, F., & Alouini, M. S. (October 2013). Error rates of M-PAM and M-QAM in generalized fading and generalized Gaussian noise environments. IEEE Communications Letters, 17(10), 1932–1935.

  19. Ayat, M., Mirzakuchaki, S., & Beheshti-Shirazi, A. (August 2016). Design and implementation of high throughput, robust, parallel M-QAM demodulator in digital communication receivers. IEEE Transactions on Circuits and Systems I: Regular Papers, 63(8), 1295–1304.

  20. Araújo, E. R., Queiroz, W. J. L., Madeiro, F., Lopes, W. T. A., & Alencar, M. S. (2015). On gated Gaussian impulsive noise in \(M\)-QAM with optimum receivers. Journal of Communication and Information Systems, 30(1), 10–20.

    Article  Google Scholar 

  21. Goldsmith, A. (2005). Wireless communications. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  22. Cho, K., & Yoon, D. (2002). On the general BER expression of one-and two-dimensional amplitude modulations. IEEE Transactions on Communications, 50(7), 1074–1080.

    Article  Google Scholar 

  23. Craig, J. W. (1991). A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations. In Proceedings of military communications conference (MILCOM’91) (pp. 571–575).

  24. Gradshteyn, I. S., & Ryzhik, I. M. (1979). Table of integrals, series, and products. Cambridge: Academic.

    Google Scholar 

  25. Fikioris, G. (2006). Integral evaluation using the Mellin transform and generalized hypergeometric functions: Tutorial and applications to antenna problems. IEEE Transactions on Antennas and Propagation, 54(12), 3895–3907.

    Article  Google Scholar 

  26. Pearson, J. (September 2009). Computation of hypergeometric functions. Master’s thesis, Worcester College, University of Oxford, Oxford.

  27. Robalo, T. C. G. (2006). Séries Hipergeométricas Generalizadas no Contexto da Teoria das Funções Hipercomplexas. Master’s thesis, Universidade de Aveiro, Aveiro.

  28. Queiroz, W. J. L., Alencar, M. S., Lopes, W. T. A., & Madeiro, F. (October 2010). Error probability in multichannel reception with \(M\)-QAM, \(M\)-PAM and R-QAM schemes under generalized fading. IEICE Transactions on Communications, E93-B(10), 2677–2877.

  29. Queiroz, W. J. L., Madeiro, F., Lopes, W. T. A., & Alencar, M. S. (May 2013). Performance analysis of generalized QAM modulation under \(\eta -\mu \) and \(\kappa -\mu \) fading. EURASIP Journal on Advances in Signal Processing, 2013(1), 1–10.

  30. Alouini, M. S., & Goldsmith, A. J. (1999). A unified approach for calculating error rates of linearly modulated signals over generalized fading channels. IEEE Transactions on Communications, 47(9), 1324–1334.

    Article  Google Scholar 

  31. Ropokis, G. A., Rontogianis, A. A., Mathiopoulos, P. T., & Berberidis, K. (September 2010). An exact performance analysis of MRC/OSTBC over generalized fading channels. IEEE Transactions on Communications, 58(9), 2486–2492.

  32. Ulusoy, A. H., & Rizaner, A. (April 2008). Adaptive path selective fuzzy decorrelating detector under impulsive noise for multipath fading CDMA systems. IEEE Communications Letters, 12(4), 228–230.

  33. Liu, X., & Bialkowski, M. E. (2010). Effect of antenna mutual coupling on MIMO channel estimation and capacity. International Journal of Antennas and Propagation, 2010, 1–9. Article ID 306173.

    Google Scholar 

Download references

Acknowledgements

The authors would like to express their thanks to the National Council for Research and Development (CNPq), the Coordination for the Improvement of Higher Education Personnel (CAPES), the Institute of Advanced Studies in Communications (Iecom), the Graduate Program in Electrical Engineering, Federal University of Campina Grande (PPgEE), and the Graduate School of Electrical Engineering, Federal University of Bahia (PPGEE), for the financial support of this research.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Federal University of Campina Grande, Campina Grande, Brazil

    Wamberto J. L. Queiroz & Marcelo S. Alencar

  2. Polytechnique School of Pernambuco, University of Pernambuco, Recife, Brazil

    Francisco Madeiro

  3. Department of Electrical Engineering, Federal University of Paraíba, João Pessoa, Brazil

    Waslon T. A. Lopes

  4. Department of Electrical Engineering, Federal University of Bahia, Salvador, Brazil

    Marcelo S. Alencar

Authors
  1. Wamberto J. L. Queiroz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francisco Madeiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Waslon T. A. Lopes
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Marcelo S. Alencar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Waslon T. A. Lopes.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Queiroz, W.J.L., Madeiro, F., Lopes, W.T.A. et al. On the performance of M-QAM for Nakagami channels subject to gated noise. Telecommun Syst 68, 1–10 (2018). https://doi.org/10.1007/s11235-017-0371-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11235-017-0371-7

Keywords

Search

Navigation