Abstract
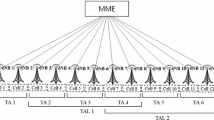
LTE networks consist of tracking areas (TAs) or a group of cells, while several TAs constitute a TA list (TAL). The LTE network adopts TAL-based registration, where, if the user equipment (UE) enters a TA that is not in its current TAL, the UE registers the TA to inform the network of its new location. A central policy for TAL allocation, known as a TA-based central policy, was proposed for TAL-based registration. Under the central policy, the TA in which the UE registers its location becomes the central TA of the new TAL. This policy can lessen the possibility of the UE quickly exiting the new TAL. However, considering the actual network architecture, it makes TAL-based registration a challenge to implement. Thus to mitigate this problem, a cell-based central policy is proposed. This study investigates TAL-based registration with cell-based central policy (TbRcc) for LTE networks. TAL-based registration with cell-based central policy and single-cell TA (TbRcc1c) is also proposed to reduce the registration cost and make up the optimal TAL. Furthermore, an improved analysis model is presented to reflect the effect of the implicit registration of calls and obtain the exact cost. Comparing the performance of the proposed scheme with those of classical TAL-based registration and distance-based registration, the performance of the proposed scheme is shown to improve. The results of this study can help research that addresses the mobility management of next-generation networks, as well as LTE networks.














Similar content being viewed by others
References
3GPP (2014) General packet radio service (GPRS) enhancements for evolved universal terrestrial radio access network (E-UTRAN) access (Release 13), third-generation partnership project, sophia antipolis cedex, France. Tech Spec Group Serv Syst Aspects 3GPP TS 23.401 V13.1.0
Chung YW (2011) Adaptive design of tracking area list in LTE. In: Eighth International Confrence on Wireless and Optical Communications Networks, pp. 1–5. https://doi.org/https://doi.org/10.1109/WOCN.2011.5872964
Deng T, Wang X, Fan P, Li K (2016) Modeling and performance analysis of a tracking-area-list-based location management scheme in LTE networks. IEEE Trans Veh Technol 65(8):6417–6431. https://doi.org/10.1109/TVT.2015.2473704
Grigoreva E, Xu J, Kellerer W (2017) Reducing mobility management signaling for automotive users in LTE Advanced. In: IEEE international symposium on local and metropolitan area networks, pp 1–6
Chen L, Liu HL, Fan Z, Xie S, Goodman ED (2017) Modeling the tracking area planning problem using an evolutionary multi-objective algorithm. IEEE Comput Intell Mag 12(1):29–41
Jung J, Baek JH (2018) Modeling and cost analysis of zone-based registration in mobile cellular networks. ETRI J 40(6):1–11
Liou RH, Lin YB (2013) Mobility management with the central-based location area policy. Comput Netw 57(4):847–857. https://doi.org/10.1016/j.comnet.2012.11.003
Alsaeedy AAR, Chong EKP (2019) Mobility management for 5G IoT devices: improving power consumption with lightweight signaling overhead. IEEE Internet Things J 6:8237–8247
Alsaeedy AAR, Chong EKP (2019) Tracking area update and paging in 5g networks: a survey of problems and solutions. Mob Netw Appl 24(2):578–595
Alsaeedy AAR, Chong EKP (2020) 5G and UAVs for mission-critical communications: swift network recovery for search-and-rescue operations. Mob Netw Appl 25:2063–2081. https://doi.org/10.1007/s11036-020-01542-2
Lin YB, Liou RH, Chang CT (2015) A dynamic paging scheme for long-term evolution mobility management. Wirel Commun Mob Comput 15(4):629–638. https://doi.org/10.1002/wcm.2371
Liou RH, Lin YB, Tsai SC (2013) An investigation on LTE mobility management. IEEE Trans Mob Comput 12(1):166–176. https://doi.org/10.1109/TMC.2011.255
Jung J, Baek JH (2018) Reducing paging cost of tracking area list-based mobility management in LTE network. J Supercomput 76:7921–7935. https://doi.org/10.1007/s11227-018-2303-z
Seo KH, Baek JH, Eom CS, Lee W (2020) optimal management of distance-based location registration using embedded markov chain. Int J Distrib Sens Netw 16(2):1550147720904611
Mao Z, Douligeris C (2000) A location-based mobility tracking scheme for PCS networks. Comput Commun 23:1729–1739
Wang X, Lei X, Fan P, Hu RQ, Horng SJ (2014) Cost analysis of movement-based location management in PCS networks: an embedded markov chain approach. IEEE Trans Veh Technol 63:1886–1902
Ross S (2014) Introduction to probability models, 11th edn. Elsevier, Amsterdam
Baek JH, Lee TH, Kim JS (2013) Performance analysis of 2-location distance-based registration in mobile communication networks. IEICE Trans Commun 96:914–917
Acknowledgements
This research was supported by Research Base Construction Fund Support Program funded by Jeonbuk National University in 2020. This research was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2016R1D1A1B01014615), and by the Ministry of Science, ICT and Future Planning (2017R1E1A1A03070134).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jang, HS., Baek, J.H. Optimal TAL-based registration with cell-based central policy in mobile cellular networks: a semi-Markov process approach. J Supercomput 77, 9172–9189 (2021). https://doi.org/10.1007/s11227-021-03624-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-021-03624-8