α-Probabilistic flexible aggregate nearest neighbor search in road networks using landmark multidimensional scaling

Abstract

In spatial database and road network applications, the search for the nearest neighbor (NN) from a given query object q is the most fundamental and important problem. Aggregate nearest neighbor (ANN) search is an extension of the NN search with a set of query objects $Q = \{ q_0, \dots , q_{M-1} \}$ and finds the object $p^*$ that minimizes $g \{ d(p^*, q_i), q_i \in Q \}$, where g (max or sum) is an aggregate function and d() is a distance function between two objects. Flexible aggregate nearest neighbor (FANN) search is an extension of the ANN search with the introduction of a flexibility factor $\phi \, (0 < \phi \le 1)$ and finds the object $p^*$ and the set of query objects $Q^*_\phi$ that minimize $g \{ d(p^*, q_i), q_i \in Q^*_\phi \}$, where $Q^*_\phi$ can be any subset of Q of size $\phi |Q|$. This study proposes an efficient $\alpha$-probabilistic FANN search algorithm in road networks. The state-of-the-art FANN search algorithm in road networks, which is known as IER-$k\hbox {NN}$, used the Euclidean distance based on the two-dimensional coordinates of objects when choosing an R-tree node that most potentially contains $p^*$. However, since the Euclidean distance is significantly different from the actual shortest-path distance between objects, IER-$k\hbox {NN}$ looks up many unnecessary nodes, thereby incurring many calculations of ‘expensive’ shortest-path distances and eventually performance degradation. The proposed algorithm transforms road network objects into k-dimensional Euclidean space objects while preserving the distances between them as much as possible using landmark multidimensional scaling (LMDS). Since the Euclidean distance after LMDS transformation is very close to the shortest-path distance, the lookup of unnecessary R-tree nodes and the calculation of expensive shortest-path distances are reduced significantly, thereby greatly improving the search performance. As a result of performance comparison experiments conducted for various real road networks and parameters, the proposed algorithm always achieved higher performance than IER-$k\hbox {NN}$; the performance (execution time) of the proposed algorithm was improved by up to 10.87 times without loss of accuracy.

1 Introduction

The search for the nearest neighbor (NN) in spatial database and road network applications is the most fundamental and important problem and has been studied extensively for many years [1,2,3,4]. With the recent advances and wide use of mobile devices and GPS systems, studies on various applications and services using the NN search are being actively conducted. The conventional NN search finds the nearest object $p^* \, (\in {\mathcal {D}})$ from a query object q among target objects ${\mathcal {D}}= \{ p_0, \dots , p_{N-1} \}$ [1, 5]. In other words, for all objects $p_j \, (0 \le j < N)$ in ${\mathcal {D}}$, it holds that $d(p^*, q) \le d(p_j, q)$, where d() is a distance function between two objects.

Aggregate nearest neighbor (ANN) search is an extension of the NN search with $M \, (\ge 1)$ query objects $Q = \{ q_0, \dots , q_{M-1} \}$, where $M = |Q|$ [2, 4, 6, 7]. The ANN search finds the object $p^*$ that minimizes g(p, Q) among target objects, where g is an aggregate function (max or sum), and g(p, Q) is defined as $g(p, Q) = g \{ d(p, q_i), q_i \in Q \}$. In other words, it holds that $g(p^*, Q) \le g(p_j, Q)$ for every object $p_j$ in ${\mathcal {D}}$. The existing studies only considered $g = \hbox {max}$ and sum; for $g = \hbox {min}$ and count, the search is trivial, and for $g =$ average, it is almost the same as that for $g =$ sum. When $M = 1$, the ANN search is identical to the NN search. The following are application examples of the ANN search:

• To quickly convene all members for an emergency meeting, it is advantageous to select a location that minimizes the (maximum) distance of the farthest member.

• To maximize the profit from customers when constructing a new building (e.g., hospital and supermarket), the location of the new building should be determined such that the sum of distances from all potential customers should be minimized.

Flexible aggregate nearest neighbor (FANN) search was investigated in [3, 8, 9], which introduced a flexibility factor $\phi \, (0 < \phi \le 1)$ to extend the ANN search. The FANN search finds the object $p^*$ and the query subset $Q^*_\phi$ that minimize $g(p, Q_\phi ) \, (Q_\phi \subset Q)$. In other words, for every object $p_j$ in ${\mathcal {D}}$ and every subset $Q_\phi$ of Q, it holds that $g(p^*, Q^*_\phi ) \le g(p_j, Q_\phi )$. In the applications of the ANN search described above, if the emergency meeting can be held only with $\phi M$ members or if $\phi M$ key customers are targeted rather than all potential customers, the FANN search is more useful and efficient than the ANN search. If $\phi = 1$, the FANN search is identical to the ANN search. If the FANN search problem is solved simply using an ANN algorithm, the ANN algorithm must be executed for every possible $Q_\phi \, (\subset Q)$. Since the number of $Q_\phi$, which is $\left( {\begin{array}{c}|Q|\\ |Q_\phi |\end{array}}\right)$, is extremely large, this approach is highly inefficient. For instance, for |Q| = 1024 and $\phi$ = 0.5, the ANN algorithm must be executed $4.48 \times 10^{306}$ times.

The previous ANN and FANN algorithms were studied separately for Euclidean spaces and road networks. The road network is usually represented using a graph data structure; each object, i.e., a point of interest (POI) corresponds to a vertex, and each physical/logical path between adjacent objects corresponds to an edge. The distance between two objects in road networks is defined as the shortest-path distance between them. The Dijkstra’s algorithm, which is a representative shortest-path algorithm, has a complexity as high as $O(E + V \log V)$, where V and E are the numbers of vertices and edges, respectively [10]. Although there are more efficient shortest-path algorithms proposed recently, their complexities are much higher than that of distance calculation between two points in a Euclidean space. Yao et al. [3] proposed various exact and approximate FANN algorithms and experimentally demonstrated that the algorithm, known as IER-$k\hbox {NN}$, using the R-tree [5] had the highest performance for almost all road networks and parameters. IER-$k\hbox {NN}$ used the Euclidean distance based on two-dimensional (2-D) coordinates of objects when choosing the R-tree node that most potentially contains $p^*$. However, since the Euclidean distance between two objects is significantly different from the shortest-path distance between them, IER-$k\hbox {NN}$ incurs many unnecessary node lookups and many calculations of ‘expensive’ shortest-path distances.

This study proposes an efficient FANN search algorithm in road networks. The contributions of this study are summarized as follows:

• The proposed algorithm uses landmark multidimensional scaling (LMDS) [11, 12] to transform all objects in a road network into k-dimensional objects $(k \ge 1)$ such that the distances between the objects are preserved as much as possible. The Euclidean distances between objects after LMDS transformation can be obtained very quickly and accurately. Since the proposed algorithm uses a more accurate distance than the state-of-the-art IER-kNN algorithm when choosing an R-tree node to visit, unnecessary node lookups and calculations of shortest-path distances are significantly reduced, thereby greatly improving the FANN search performance of the proposed algorithm.

• The correctness of the proposed algorithm is proven based on a probabilistic assumption. The proposed algorithm is probabilistic in the sense that, for a given probability $\alpha$, it ‘assumes’ the interval of differences between the actual shortest-path distances and the estimated k-dimensional Euclidean distances.

• A series of experiments were conducted to compare the performance of the proposed algorithm and the state-of-the-art IER-$k\hbox {NN}$ algorithm using various real road networks. As a result, the proposed algorithm always achieved higher performance for all road networks and parameters than IER-$k\hbox {NN}$; the performance (execution time) of the proposed algorithm was improved by up to 10.87 times without loss of accuracy.

This paper is organized as follows: Sect. 2 briefly describes the previous ANN and FANN search algorithms and LMDS. Section 3 explains the proposed algorithm in detail, and Sect. 4 evaluates the performance of the proposed algorithm. Finally, Sect. 5 concludes this paper.

2 Related work

This section briefly introduces the previous ANN and FANN search algorithms in Euclidean spaces and road networks. Thereafter, it explains multidimensional scaling (MDS) that transforms objects in a metric space into those in a Euclidean space.

Yiu et al. [4] proposed three algorithms for the ANN search in road networks. The first algorithm was designed by applying the Incremental Euclidean Restriction (IER) paradigm; it prunes an R-tree node n based on the Euclidean distances from the node n to query objects. The remaining two algorithms were adaptations of the existing top-k algorithm, which finds the k nearest query objects based on their shortest-path distances. Ioup et al. [2] proposed an algorithm for the ANN search in road networks using the M-tree [13]. However, this algorithm returns only approximate search results, and the error range of the search results is not known.

Li et al. [8, 9] investigated the FANN search in Euclidean spaces. They presented two exact algorithms, namely the R-tree algorithm and the list algorithm. Li et al. [8, 9] also proposed a 3-approximate algorithm and a $(1+2\sqrt{2})$-approximate algorithm for aggregate functions $g =$ sum and max, respectively. Li et al. [9] additionally presented a 2-approximate algorithm in a 2-D space and a $(1+\epsilon )$-approximate algorithm in a low-dimensional space for each of $g =$ sum and max.

Yao et al. [3] handled the FANN search in road networks and proposed three algorithms, namely Dijkstra-based algorithm, R-List algorithm, and the IER-$k\hbox {NN}$ algorithm. In addition, they presented an exact algorithm and a 2-approximate algorithm requiring no indices for $g = \hbox {max}$ and sum, respectively. Among these algorithms, IER-$k\hbox {NN}$ showed almost always the highest performance. However, as in [4], IER-$k\hbox {NN}$ used an index constructed using 2-D Euclidean coordinates instead of the actual shortest-path distances between objects. The algorithms requiring no indices showed very low search performance as expected.

MDS [14, 15] is a method of transforming objects in a metric space into objects (i.e., points) in a k-dimensional Euclidean space while preserving the distances between objects as much as possible, where $k \, (\ge 1)$ can be given arbitrarily. MDS is also used for dimensionality reduction and visualization for objects in a high-dimensional Euclidean space. Classical MDS [14], which is most widely known, has the advantage of providing highly accurate transformation results, but it also has the disadvantage of very high time complexity of $O(CN^2 + N^3)$, where N is the number of objects and C is the cost for distance calculation. LMDS [11, 12] was proposed to overcome the disadvantage of classical MDS. Classical MDS requires a distance matrix of size $N \times N$ for every possible object pair, but LMDS uses only a distance matrix of size $N \times n$ for every combination between randomly chosen $n \, (\ll N)$ ‘landmark’ objects and all objects, and has the time complexity of $O(CnN + knN + n^3)$, which is much lower than that of classical MDS. The efficiency and accuracy of LMDS have been demonstrated in [12, 15]. Section 4 also demonstrates experimentally that LMDS significantly improves FANN search performance.

3 IER-LMDS: Efficient FANN algorithm in road networks

This section explains in detail the proposed FANN algorithm, which is referred to as IER-LMDS hereinafter. The IER-LMDS algorithm greatly improves FANN search performance by significantly reducing the calculations of expensive shortest-path distances between two objects compared with IER-$k\hbox {NN}$ [3]. Table 1 summarizes the notations used in this study.

Table 1 Summary of notations

In this study, road network objects are mapped into those in a metric space as in [2]. The metric space is formally defined as a $({\mathcal {D}}, d)$ pair, where ${\mathcal {D}}$ is a set of objects, and $d: {\mathcal {D}}\times {\mathcal {D}}\rightarrow {{\mathbb {R}}}$ is a distance function between two arbitrary objects in ${\mathcal {D}}$ satisfying the following three properties for any objects $O_a, O_b$, and $O_c \, (\in {\mathcal {D}})$:

• $d(O_a, O_b) = d(O_b, O_a)$   (symmetry)

• $d(O_a, O_b) > 0 \, (a \ne b)$ or $d(O_a, O_a) = 0$   (non-negativity)

• $d(O_a, O_b) \le d(O_a, O_c) + d(O_b, O_c)$   (triangle inequality)

The shortest-path distance between road network objects satisfies the above three properties if all edges are undirected edges with positive weights and there is no self-loop edge. We consider only the road networks satisfying the conditions in this study.

Algorithm 1 outlines the IER-LMDS algorithm. The basic architecture is similar to that of the previous FANN algorithms in Euclidean spaces and road networks [3, 9]. IER-LMDS and the previous algorithms commonly store the nodes n of the R-tree in a priority queue H and extract them from H in the order of $n.{\hat{g}}_\phi$ (line 6 of Algorithm 1), where $n.{\hat{g}}_\phi$ is the estimated FANN distance of node n (explained in detail later), and is obtained using the estimated distance ${\hat{d}}$ between two objects. It is obvious that the estimated distance ${\hat{d}}$ that is closer to the actual shortest-path distance d is more advantageous for reducing the lookups of unnecessary nodes n and the calculations of ‘expensive’ distances d for the objects in the nodes n.

While IER-$k\hbox {NN}$ uses the Euclidean distance ${\hat{d}}_{(2)}$ based on 2-D coordinates of objects when calculating $n.{\hat{g}}_\phi$, IER-LMDS uses the Euclidean distance ${\hat{d}}_{(k)}$ based on the k-dimensional coordinates of objects obtained through LMDS transformation. While the distance ${\hat{d}}_{(2)}$ is significantly different from the actual shortest-path distance d, the distance ${\hat{d}}_{(k)}$ is very close to d as explained in Sect. 2. This is quantitatively shown using real road network datasets in Sect. 4.

Figure 1 shows an example of distribution of $X = d - {\hat{d}}_{(k)}$ for a sample of 10,000 object pairs obtained after LMDS transformation of a real road network dataset. As shown in this figure, the sample mean ${\bar{X}}$ is very close to 0, and the sample standard deviation S is also very small. To identify the distribution of X, we conducted Kolmogorov–Smirnov tests (K–S tests) [16] for diverse probability distributions. The K–S test for a probability distribution returns the ‘goodness-of-fit’ statistic, which represents the difference between the given sample data and the specified probability distribution function values. Our tests yielded the best statistics for the normal distribution and Student’s t-distribution. Since the t-distribution becomes closer to a normal distribution as the degree of freedom $\nu \, (= n - 1)$ increases, where n is the number of samples, we assume that X follows a normal distribution. The mean and standard deviation of the population are estimated as those obtained from a sample of a sufficiently large size, i.e., it is assumed that $X \sim {{\mathcal {N}}}({\bar{X}}, S^2)$.

Fig. 1

Example of distribution of $X \, (= d - {\hat{d}}_{(k)})$

Each line of Algorithm 1 is explained in detail as follows: first, LMDS transformation is performed for the given road network dataset ${\mathcal {R}}$. For LMDS, two parameters n and $k \, (\le n)$ are required as described in Sect. 2. The values of these two parameters are directly proportional to accuracy of the LMDS transformation. However, the larger values of these two parameters generally lead to a longer transformation time. In particular, if k becomes very large, the search performance is dramatically degraded when using a multi-dimensional index such as the R-tree constructed using the k-dimensional objects. This phenomenon is known as the high-dimensionality problem or high-dimensionality curse [17]. In the experiments in Sect. 4, n and k were set as n = 50 and $k = 4$. After storing all the k-dimensional objects in an R-tree, the root node of the R-tree is stored in the priority queue H, and the FANN distance ${\hat{p}}^*.g_\phi$ of the object ${\hat{p}}^*$ is set to infinity.

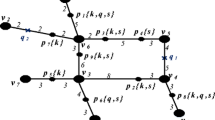
The while loop in lines 5–16 of Algorithm 1 is performed once for every node n that has not been pruned in H. In line 6, the node with the smallest $n.{\hat{g}}_\phi$ is extracted among all nodes n in H. If n is a non-leaf node, $e.{\hat{g}}_\phi$ is calculated for every entry (i.e., node) e in n in line 9 as follows: For each query object $q_i \, (\in Q, 0 \le i < M)$, the Euclidean distance ${\hat{d}}$, i.e., ${\hat{d}}_{(k)}$ between $q_i$ and the MBR e.R for e is obtained, where the distance ${\hat{d}}(q_i, e.R)$ is defined as ${\hat{d}}(q_i, e.R) = \sqrt{{{\textit{mindist}}} (q_i, e.R)}$. IER-LMDS as well as many other FANN algorithms [3, 9] uses the definition of mindist() as given in [5]. Figure 2 shows the examples of ${\hat{d}}$ distances for three query objects. The ${\hat{d}}$ distance of an object residing inside of the MBR such as $q_3$ is defined as 0. Among M ${\hat{d}}$ values, the smallest $m \, (= \phi |Q|)$ values are obtained, and without loss of generality, let ${\hat{d}}_0, \dots , {\hat{d}}_{m-1}$ be the smallest m ${\hat{d}}$ values. Thereafter, we obtain $e.{\hat{g}}_\phi = g \{ {\hat{d}}_i, 0 \le i < m \}$ [3, 9], where g = max or sum. If the value of $e.{\hat{g}}_\phi$ is less than or equal to ${\hat{p}}^*.g_\phi - \kappa ({\bar{X}} + z_\alpha S)$, e is added in H, where $\kappa$ is 1 if g = max or m if g = sum. ${\bar{X}}$ and S are the sample mean and standard deviation for variable X, respectively, and $z_\alpha$ is the value that satisfies the probability $P(z_\alpha \le Z) = \alpha$ for the given $\alpha$ and the variable Z that follows the standard normal distribution. The following Lemma 1 proves that there is no false drop (i.e., false negative) by IER-LMDS if the variable X follows the normal distribution ${\mathcal {N}}({\bar{X}}, S^2)$ as was assumed above.

Fig. 2

${\hat{d}}$ distances for three query objects

Lemma 1

If the variable $X \, (= d - {\hat{d}})$ follows the normal distribution ${\mathcal {N}}({\bar{X}}, S^2)$, there is no false drop in line 9 of Algorithm 1.

Proof

In line 9, ${\hat{d}}(q_i, e.R)$ is calculated for each query object $q_i$, and $e.{\hat{g}}_\phi$ is obtained using the m smallest ${\hat{d}}$ values $(m = \phi |Q|)$. Without loss of generality, let $q_0, \dots , q_{m-1}$ be the query objects with the smallest m ${\hat{d}}$ values, and ${\hat{d}}_0, \dots , {\hat{d}}_{m-1}$ be their ${\hat{d}}$ values. In addition, let ${\hat{d}}'_0, \dots , {\hat{d}}'_{m-1}$ and $d_0, \dots , d_{m-1}$ be the ${\hat{d}}$ and d values, respectively, between each $q_i$ and an arbitrary object $e'$ in the MBR e.R. Then, it holds that ${\hat{d}}_i \le {\hat{d}}'_i$ for every $q_i \, (0 \le i < m)$.

For the given probability $\alpha \, (0< \alpha < 1)$, $z_\alpha$ is the value that satisfies $P \left( z_\alpha \le \frac{X - {\bar{X}}}{S} \right) = \alpha$. In other words, it holds that ${\bar{X}} + z_\alpha S \le X$ for the given $\alpha$. By replacing X with $d_i - {\hat{d}}'_i$ for two objects $q_i$ and $e'$, we obtain ${\hat{d}}'_i + {\bar{X}} + z_\alpha S \le d_i$ and thus $g \{ {\hat{d}}'_i + {\bar{X}} + z_\alpha S \} \le g \{ d_i \}$. Since it holds that ${\hat{d}}_i \le {\hat{d}}'_i$, it is induced that $g \{ {\hat{d}}_i + {\bar{X}} + z_\alpha S \} \le g \{ {\hat{d}}'_i + {\bar{X}} + z_\alpha S \}$, i.e., $e.{\hat{g}}_\phi + \kappa ({\bar{X}} + z_\alpha S) \le g \{ {\hat{d}}'_i + {\bar{X}} + z_\alpha S \}$, and thus $e.{\hat{g}}_\phi + \kappa ({\bar{X}} + z_\alpha S) \le g \{ d_i \}$, where $\kappa = 1 \, (g = \max )$ or $m \, (g = \text{ sum})$. Therefore, if it holds that ${\hat{p}}^*.g_\phi < e.{\hat{g}}_\phi + \kappa ({\bar{X}} + z_\alpha S)$, i.e., $e.{\hat{g}}_\phi > {\hat{p}}^*.g_\phi - \kappa ({\bar{X}} + z_\alpha S)$, it is concluded that ${\hat{p}}^*.g_\phi < g \{ d_i \}$ for any $e'$ in e.R, and thus e can be discarded safely. $\square$

If the node n extracted from H in line 6 is a leaf node, in line 13, $e.g_\phi$ is calculated for every entry (i.e., object) e in n. The $e.g_\phi$ value is calculated in the same manner as $e.{\hat{g}}_\phi$ in line 9, except that the actual shortest-path distance d is used instead of ${\hat{d}}$. In other words, $e.g_\phi$ is obtained as $e.g_\phi = g \{ d_i, 0 \le i < m \}$ [3, 9], where $d_i = d(q_i, e)$, and without loss of generality, $d_i \, (0 \le i < m)$ are the m smallest values among $d_i \, (0 \le i < M)$. If $e.g_\phi$ is smaller than ${\hat{p}}^*.g_\phi$, e is assigned as a new ${\hat{p}}^*$. Finally, in line 17, the current ${\hat{p}}^*$ value is returned as $p^*$, and the corresponding $Q^*_\phi$ and $p^*.g_\phi \, (= g(p^*, Q^*_\phi ))$ are also returned together.

In Algorithm 1, the number of FANN objects (k) was assumed to be 1. This algorithm can be extended for the general case of $k \ge 1$ as follows: instead of storing only one final FANN object ${\hat{p}}^*$, an array K is allocated to store k FANN objects. The ${\hat{p}}_i^*$ objects in K are sorted in the order of ${\hat{p}}_i^*.g_\phi$, and initially, the algorithm sets ${\hat{p}}_i^*.g_\phi \leftarrow \infty \, (0 \le i < k)$ in line 4. In lines 9 and 13, ${\hat{p}}^*.g_\phi$ is replaced with ${\hat{p}}_{k-1}^*.g_\phi$, and finally, the array K is returned in line 17.

Similar to IER-$k\hbox {NN}$, IER-LMDS needs to compute an FANN distance $g(p, Q_\phi )$ for every object p in a road network ${\mathcal {R}}$ in the worst case. The FANN distance $g(p, Q_\phi )$ for an object p is obtained by finding $k \, (= \phi M)$ query objects in Q nearest to p and then computing the aggregate of the shortest-path distances of the k query objects. Thus, the complexity of IER-LMDS is O(KN), where K is the cost of the k-NN search and N is the number of objects in ${\mathcal {R}}$ [3]. The k-NN search also needs to calculate the shortest-path distances to all query objects in the worst case. Therefore, the complexity of IER-LMDS can be rewritten as O(CMN), where C is the cost of a shortest-path distance calculation and M is the number of query objects. Since M and N are set as constants, the performance of both algorithms is determined by the total number of shortest-path distance calculations conducted in the algorithms.

4 Experimental evaluation

In this section, the search performance of IER-LMDS is compared with that of IER-$k\hbox {NN}$ [3] through a series of experiments using real road network datasets. Since IER-$k\hbox {NN}$ showed the best performance among the algorithms by Yao et al. [3], IER-LMDS is compared only with IER-$k\hbox {NN}$ in this study. The search accuracy of IER-LMDS is also examined for various search probabilities $\alpha$. The platform for the experiments is a workstation with an AMD 3970X CPU, 128 GB memory, and 1.2TB SSD. We implemented IER-LMDS and IER-$k\hbox {NN}$ in C/C++. In particular, we used a library named Eigen for eigendecomposition of distance matrices in LMDS.¹ In all experiments, the parameters for LMDS were set as $n = 50$ and $k = 4$.

The datasets used in the experiments are actual road networks of five states and Washington DC in the US. These datasets were provided by the US Census Bureau and have been used in the 9th DIMACS Implementation Challenge² and in many previous studies [1, 3]. Table 2 lists the datasets used in the experiments. Each dataset is a graph composed of a set of vertices and a set of undirected edges. Each vertex corresponds to an object (i.e., a POI) and is composed of an ID and a geographic coordinate (latitude and longitude). Each edge corresponds to a path directly connecting two adjacent vertices and is composed of the IDs of two connected vertices, transportation time, geographic distance, and road type. The datasets have noises such as self-loop edges and disconnected graph segments [3]. Thus, we performed pre-processing tasks to remove the noises.

Table 2 Road network datasets

The distance d() between two objects in a road network was defined as the shortest-path distance between them and was obtained using the pruned highway labeling (PHL) algorithm [18, 19]. The PHL algorithm is known as the fastest shortest-path algorithm [1, 3]. In the experiments, we used the C/C++ code written by the original authors of the PHL algorithm.³

In the first experiment, stress values were calculated using the actual shortest-path distances d and the estimated Euclidean distances ${\hat{d}}$ between two objects in road networks. We compared the stress values that were separately calculated using ${\hat{d}}_{(k)}$ and ${\hat{d}}_{(2)}$ distances, where ${\hat{d}}_{(k)}$ is the k-dimensional distance obtained after LMDS transformation, and ${\hat{d}}_{(2)}$ is the distance obtained using 2-D coordinates of objects (refer to Sect. 3). The stress function is defined as Eq. (1) [20]:

$$\begin{aligned} {{\textit{Stress}}}^2 = \frac{\sum \left( d_{i,j} - {\hat{d}}_{i,j} \right) ^2}{\sum d_{i,j}^2} \, , \end{aligned}$$

(1)

where $d_{i,j}$ and ${\hat{d}}_{i,j}$ represent the actual shortest-path distance and the Euclidean distance between two objects $O_i$ and $O_j$, respectively. In both IER-LMDS and IER-$k\hbox {NN}$, since it is advantageous that the estimated distance ${\hat{d}}$ is close to the actual distance d, the smaller stress values are better. Table 3 summarizes the result of the first experiment. Each value is the average of stress values obtained for randomly chosen 1% of all possible paths or 100 million paths, whichever is larger, from each road network. The stress values in the second and third columns were calculated using ${\hat{d}}_{(k)}$ and ${\hat{d}}_{(2)}$ distances, respectively. The result showed that the stress values decreased significantly when LMDS transformation was applied for every road network. Therefore, it is clear that IER-LMDS can determine the pruning bounds of R-tree nodes more accurately than IER-$k\hbox {NN}$, thereby significantly reducing the calculation of expensive shortest-path distances d.

Table 3 Comparison of stress values

In the second experiment, we compare the calculation time of the shortest-path distance d and the Euclidean distance ${\hat{d}}$. Table 4 summarizes the result of the second experiment, where the ratios are obtained by dividing the calculation time of distance d by that of distance ${\hat{d}}$. As in the first experiment, each value is the average of ratios obtained by randomly chosen 1% of all possible paths or 100 million paths in each road network. The ratio tends to increase as the road network becomes larger since the size of a road network is directly proportional to the number of objects on the path between two objects on the average. Therefore, it is essential to reduce the calculation of distance d to improve the performance of any FANN search algorithm.

Table 4 Ratios of distance calculation time

Table 5 lists the parameters to consider in the third to eighth experiments. The parameter values in parentheses indicate default values. In the third experiment, we compared the execution time required for the FANN search and the number of PHL distance calculations for each road network dataset in Table 2. The values of all other parameters were set as default. Figure 3 shows the result of the third experiment. Each value in this figure is the average of the values obtained for randomly generated 1000 query sets Q. The result for each of aggregate functions g = max and sum was indicated by appending suffixes ‘-MAX’ and ‘-SUM’ to algorithm names, respectively, e.g., IER-LMDS-MAX and IER-LMDS-SUM. As can be observed in this figure, the execution time and the number of PHL distance calculations have similar trends for both algorithms. This indicates that the most dominant factor that determines the performance of the FANN algorithms is the number of shortest-path distance calculations. As the size of road network increased, more objects are contained within the pruning boundaries causing more distance d calculations, thereby increasing the execution time. In the third experiment, IER-LMDS always achieved higher performance than IER-$k\hbox {NN}$; for NH dataset and $g = \max$, the performance was improved by up to 4.37 times.

Table 5 Experimental parameters

Fig. 3

Comparison of FANN performance for various road network datasets (${\mathcal {R}}$)

In the fourth experiment, FANN search performance was compared while changing the number of query objects M, and the result is shown in Fig. 4. As M increased, the execution time and the number of PHL distance calculations increased almost linearly since in line 13 of Algorithm 1, the actual distance d to every query object $q_i$ is calculated to determine the FANN distance $e.g_\phi$ for each object e. As in the third experiment, the performance was determined almost by the number of PHL distance calculations for both algorithms. In this experiment, IER-LMDS always achieved higher performance than IER-$k\hbox {NN}$; the performance was improved by up to 2.85 times for $M = 64$ and $g = \max$.

Fig. 4

Comparison of FANN performance for various query sizes (M)

In the fifth experiment, FANN search performance was compared while changing the coverage ratio C of query objects. C was obtained by dividing the size of the minimal region containing all query objects by that of the region occupied by the entire road network. Figure 5 shows the result of the fifth experiment. As C increased, the execution time also increased generally since more objects were contained in the query region and the number of PHL distance calculations between them also increased. In this experiment as well, IER-LMDS always achieved higher performance than IER-$k\hbox {NN}$; the performance was improved by up to 3.61 times for $C = 0.2$ and $g = \max$.

Fig. 5

Comparison of FANN performance for various coverage ratios of query (C)

In the sixth experiment, the performance was compared for various flexibility factors $\phi$, and the result is shown in Fig. 6. In this figure, as $\phi$ increased, the execution time and the number of PHL distance calculations of IER-$k\hbox {NN}$ also increased since, as $\phi$ increased, ${\hat{p}}^*.g_\phi$ for the candidate FANN object ${\hat{p}}^*$ also increased causing more R-tree node lookups and more PHL distance calculations. In IER-LMDS, in contrast, although $\phi$ increased, the increasing trend of the execution time and the number of PHL distance calculations was not strong; they even decreased for $\phi$ = 0.8 and 1.0. In line 9 of Algorithm 1, although $\phi$ and ${\hat{p}}^*.g_\phi$ increased, the value of $\kappa ({\bar{X}} + z_\alpha S)$ remained constant and thus there was only a small change in the pruning bound. Meanwhile, as $\phi$ increased, $e.{\hat{g}}_\phi$ also increased for an entry e causing less entries e to be added in H. In this experiment as well, IER-LMDS always achieved higher performance than IER-$k\hbox {NN}$; the performance was improved by up to 10.87 times for $\phi = 1.0$ and $g = \max$.

Fig. 6

Comparison of FANN performance for various flexibility factors ($\phi$)

In the seventh experiment, the performance was compared while changing the number of FANN objects k. Figure 7 shows the results. For both IER-LDMS and IER-$k\hbox {NN}$, the pruning bound increased with k. Since more R-tree nodes were visited, the execution time and the number of PHL distance calculations increased. In this experiment as well, IER-LMDS always achieved higher performance than IER-$k\hbox {NN}$; the performance was improved by up to 2.79 times for $k = 1$ and $g = \max$.

Fig. 7

Comparison of FANN performance for various number of nearest neighbors (k)

Finally, FANN search performance and accuracy were compared for various search probabilities $\alpha$. The search accuracy of IER-LDMS was calculated as follows: for each query Q, the error $\epsilon = p^*.g_\phi - \rho ^*.g_\phi$ was determined, where $p^*.g_\phi$ and $\rho ^*.g_\phi$ were obtained for the FANN objects $p^*$ and $\rho ^*$ returned by IER-LDMS and IER-$k\hbox {NN}$, respectively. Subsequently, the mean square error (MSE), i.e., $\sum \epsilon ^2 / n$ was calculated, where n is the number of queries. Since the third to eighth experiments were conducted for 1000 randomly generated queries, $n = 1000$. The result of the final experiment is shown in Fig. 8. In Fig. 8a, since the pruning bound for IER-LMDS increased with $\alpha$, the number of PHL distance calculations and the execution time also increased. In Fig. 8b, we could find that MSE decreased rapidly as $\alpha$ increased. For $\alpha \ge 0.5$, all $\epsilon$ became zero. The graph of the number of PHL distance calculations is omitted since it has a similar trend to the execution time as in other experiments. In the last experiment as well, IER-LDMS always achieved higher performance than IER-$k\hbox {NN}$; the performance was improved by up to 3.13 times for $\alpha = 0.5$ and $g = \max$.

Fig. 8

Comparison of FANN performance and accuracy for various search probabilities ($\alpha$)

5 Conclusions

This study proposed an efficient $\alpha$-probabilistic FANN search algorithm named IER-LMDS in road networks. IER-LMDS mapped road network objects into those in a metric space and then transformed them into k-dimensional Euclidean space objects while preserving the distances between objects using LMDS [11, 12]. The state-of-the-art FANN algorithm named IER-$k\hbox {NN}$ [3] used the Euclidean distance based on the 2-D coordinates of objects when choosing the R-tree nodes to visit, and thus it could not avoid performance degradation due to significant differences between the Euclidean distances and the actual shortest-path distances.

A series of experiments were conducted in this study to confirm the superiority of IER-LMDS by comparing its performance and accuracy with those of IER-$k\hbox {NN}$ for various real road networks and parameters. The results of all experiments revealed that IER-LDMS always achieved higher performance than IER-$k\hbox {NN}$ for all road networks and parameters; the performance was improved by up to 10.87 times. We believe that IER-LDMS will be widely adopted for efficient FANN search in a variety of road network applications in the future.