Introduction

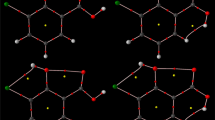
Wrackmeyer is most likely the first who paid attention to the presence and the bonding character of a Si–H–B bridge in organoboron compounds [1–4]. The role of this bridge in the formation of heterocyclic systems containing both silicon and boron atoms was discussed on the basis of both NMR and IR spectroscopic data [1]. Also, the presence of a Si–H–B bridge in 3-bora-4-methylene-homoadamantane was determined on the basis of X-ray structural measurements [2]. More importantly for the present article, based on the NMR spectra obtained for two members (1 and 2 in Fig. 1) of 1-silacyclopent-2-enes, Wrackmeyer et al. [4] have concluded that Si–H–B bridges in these molecules are either absent or extremely weak. This was to be in opposition to their 1-silacyclohex-2-ene counterparts (3 and 4 in Fig. 1), where existences of Si–H–B bridges have been confirmed by similar spectroscopic data [4]. This difference in Si–H–B bonding effect was attributed to stronger repulsion between silyl groups in both 1-silacyclohex-2-enes forcing the exocyclic relevant silyl group to approach closer to the 9-borabicyclo[3.3.1]nonane group (9-BBN) and, as a consequence, considerably reducing the H ⋯ B distance.

Fig. 1
figure 1

Structural formulas of 1-silacyclopent-2-enes and 1-silacyclohex-2-enes investigated by Wrackmeyer et al. [4]

Full size image

Bonding properties of the Si–H ⋯ Y bridge are well known [5–9]. For example, in case of Y being a transition metal, this interaction is called an agostic bond [10–13] or a σ interaction [12–17] depending on a specific situation, whereas if Y is an electron-deficient element (as, for example, boron), this type of interaction was called a “charge-inverted hydrogen bond” (CIHB) [11–13, 18–25]. Therefore, the electron-deficient Si–H–B bridge (this term was being used by Wrackmeyer et al. [1–4]) in investigated systems in fact represents one of the examples of intramolecular charge-inverted hydrogen bonds (IMCIHB).

Taking the above into account, it is really a tempting challenge to assess strengths of H ⋯ B interactions in 3 and 4, and particularly in 1 and 2. It can be done by computing values of the interaction energy of H ⋯ B. Although this energetical parameter is not accessible to experimental measurements, it is relatively easily accessible to theoretical methods of molecular modeling. As widely believed, the interaction energy directly describes the strength of a (local) intramolecular interaction. Taking into account the NMR spectroscopic data obtained by Wrackmeyer et al. [4], one should expect clearly negative, i.e. showing stabilizing character of H ⋯ B, values of interaction energies obtained for both 1-silacyclohex-2-enes, i.e. 3 and 4, whereas for both 1-silacyclopent-2-enes (1 and 2), they should be either positive or only slightly negative. In the former case, our results would suggest repulsive character of the H ⋯ B contact, whereas in the latter, this contact would be weakly bonding. In addition to these four molecules investigated earlier by Wrackmeyer et al. [4] (Fig. 1), we also have performed similar computations for their simplified derivatives (see the ’Investigated systems’ section). This approach allows us to discuss influence of both electronic and steric effects originating from the presence of specific substituents on the strength of investigated Si–H ⋯ B bridges.

The other purpose of this article is to shed light on some problems relating to the definition of the interaction energy (of an intramolecular H ⋯ Y contact) itself. In particular, an importance of the choice of a reasonable reference open system will be discussed in detail, showing that this is not so easily-done task as it might at first seem. In our opinion, this issue is not raised often enough [19, 26–31].

Computational methodology

Geometry optimizations and frequency calculations to analyze characters of obtained stationary points have been performed using Gaussian 09 program [32]. Lack of imaginary frequencies has confirmed that obtained geometries correspond to local minima on the potential energy hypersurface. For some reference systems, also, partial geometry optimizations have been performed as indicated in the text. Analysis of the topology of the electron density distribution has been made by means of quantum theory of atoms in molecules (QTAIM) [33–35] using the AIMAll package [36]. All calculations have been performed utilizing the PBE0 [37–39] exchange-correlation functional of density functional theory and the 6-311G(d,p) basis set [40, 41]. It was shown that PBE0 gives reasonable molecular structures [12, 42] as well as electronic densities [43, 44]. On the other hand, the 6-311G(d,p) basis set is of valence triple zeta quality and, additionally, includes polarization functions for all atoms.

Energy of an intramolecular interaction

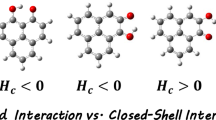
In contrast to the energy of an intermolecular interaction (e.g. a hydrogen bond), the energy of an intramolecular interaction is not a definable quantity due to the fact that any attempt of extracting the energy of the interaction of interest from the total energy of a system hosting this interaction introduces high degree of discretion for the choice of a reference system [27–31]. Nevertheless, in spite of this, some additive schemes leading to numbers understood as interaction energies have been proposed. Among them, the so-called open-closed method [45, 46] seems to be both the most popular [26–29, 45–58] and straightforward. According to this method, the interaction energy is just a difference between total energies of the closed form of a molecule, i.e. the form hosting the relevant interaction, and the open one obtained by a proper rotation of either the donor or the acceptor group and, as a consequence, characterized by a cleavage of the relevant interaction (see Fig. 2).

Fig. 2
figure 2

Scheme presenting a method for receiving open reference forms in the open-closed method defining the energy of intramolecular interaction (indicated by dashed line) in the closed form

Full size image

It is understood that in general different interaction energy values are obtained as a result of different reference open systems used [28].

What is more, having one of these open systems already chosen, one encounters a new question, namely whether or not the geometry of the open system should be fully optimized [28, 58]. Unfortunately, only in a small piece of articles where the open-closed method is utilized, this question is addressed [19, 28, 29, 45, 46, 58]. Most likely, Schuster was the first who suggested [45] to use the open form having ’the least changes in molecular geometry besides a cleavage of the H-bond‘ pointing out that the open reference system ’need not be a local minimum of the energy surface‘ [46]. In his opinion, performing single-point calculations for the open form ’seems to be more appropriate‘ than the full geometry optimization of the open reference form ’in cases where it can be applied, because it does not mix a large energy of isomerization into the H-bond energy‘ [46]. Schuster underlined, however, that any splitting of the change in total energy into pure isomerization and H-bond energy is artificial in fact [46]. As already mentioned, acceptance of this approach leads to single-point energy calculations for the open form, for which all geometry parameters (but a rotation angle of course) are taken from the closed form and then kept constant (i.e. frozen). This situation is depicted on the left hand side of Fig. 3, where E c, \(E_{\mathrm {o}}^{\text {f,c}}\) and \(E_{\mathrm {c}}^{\mathrm {f}}\) mean total energies of closed, fictitious open and fictitious closed forms, respectively. It should be noted that this approach is in line with the definition of the intermolecular interaction energy, ΔE int = E(AB) − E(A) − E(B), where individual monomers A and B have geometries from the complex AB.

On the contrary, the other approach, which nowadays seems to be a standard procedure [57], in the open-closed method arises if the full geometry optimization (rather than single-point calculations) of the open form is performed (leading to E o; Fig. 3). This approach takes into account the fact that the geometry (structure) change that takes place upon the open form → closed form transformation is a consequence of the relevant interaction. In other words, the geometry of the interaction-hosting system is marked by the presence of this interaction. In the picture of intermolecular interactions, this approach corresponds to fully isolated monomers A and B possessing their own geometries. In this case, ΔE int would include deformation energies as well. More precisely, both these ΔE int values in fact correspond to different energy parameters—interaction and binding energies, respectively. Similarly, in the case of intramolecular interactions, both approaches introduce in fact different definitions of the interaction energy—parameter that—to remind—is in fact not strictly defined by quantum chemistry [29–31]. Both these definitions of the (intramolecular) interaction energy correspond to different partition schemes of the total energy of the closed form as shown in Fig. 3. Of course, \(|E_{\mathrm {o}}| > |E_{\mathrm {o}}^{\text {f,c}}|\) and hence, one should observe that \({\Delta } E_{\text {int}}^{\text {OPT}} < {\Delta } E_{\text {int}}^{\text {SP}}\).

Fig. 3
figure 3

Scheme showing two models of the partition of the total energy of the interaction-hosting molecule (E c) to the energy of the interaction and the total energy of a fictitious molecule obtained by ’exclusion‘ of this interaction

Full size image

At this point, one encounters a new problem. Quite often reference open systems have new important interactions (either attractive or repulsive) [27–31, 51–53]. As a consequence, one obtains either under- (\({\Delta } E_{\text {int,a}}^{\text {OPT}}\)) or overestimated (\({\Delta } E_{\text {int,r}}^{\text {OPT}}\)) values of interaction energies, respectively, as shown in Fig. 4. Some examples will be discussed later.

Fig. 4
figure 4

Unreliable estimates of the interaction energy in the open-closed method obtained due to additional repulsive or attractive interactions or extended structure of the reference open form

Full size image

Moreover, in many instances, the structure of the fully optimized open form may also be considerably different than that of the closed form. This case can be manifested by significantly different values of bond lengths and of plane or dihedral angles. For example, Buemi et al. [28] rebuked the use of the most extended enol and enethiol tautomers of thiomalondialdehyde as reference structures [27] since the trans configuration of double bonds seems to be too different than the cis one in the closed form. It is easy to imagine other examples. The amino group is usually somewhat pyramidal, whereas it becomes flat in closed form featuring conjugated system of double bonds as, e.g. in 3-aminoprop-2-enal. Boryl−BH2 group may be perpendicular (or nearly so) to the molecular chain in closed form, whereas, on the contrary, it may be in plane in the open one. It will be shown that the latter happens if the 9-BNN group is substituted by -BH2. It is seen from Fig. 4 that too attractive interaction(s) in the open reference form or its significantly extended structure can even lead to changed sign of the interaction energy [19].

Taking the above into account, we proposed [19] performing partial (i.e. constrained) geometry optimization in such cases, where one freezes only those geometric parameters whose optimization would lead to either some new important interactions or to considerably different structures. Although in most cases, it is sufficiently to freeze one or two dihedral angles that determine positions of donor and acceptor groups, sometimes, it is necessary to freeze other geometrical parameters as well. Of course, the full geometry optimization of the open form may still be performed if only it will not lead to any new important interactions or considerable structural changes in at least some parts of the molecule. The idea of performing constrained geometry optimization of the open reference form [19] is also utilized in our estimates of interaction energies of H ⋯ B.

Investigated systems

Initial calculations have been performed for 9-(2-(dimethylsilyl)-1,1-diphenyl-1-silacyclopenta-2-en-3-yl)-9-borabicyclo(3.3.1)nonane (1 in Fig. 1) utilizing its experimental structure determined from X-ray crystalographic measurements [4] and available via Cambridge Structural Database [59] as MEDSUK (1A \(_{\exp }\)). Also, its analogue with −SiMe2H rotated about the Si–C bond has been used as a reference molecule (1a \(_{\exp }\)). Their fully optimized analogues are labelled as 1A and 1a, respectively. Since experimental structures of 2, 3 and 4 have not been determined, fully optimized geometries of both open and closed forms of these molecules have been obtained (2A, 3A, 4A and 2a, 3a, 4a, respectively). Although used for computing ν SiH frequency shifts, 1a, 2a, 3a and 4a have, however, been found as being not fully correct references for interaction energies. Instead, reference open systems obtained after partial (see further text) geometry optimizations have been used (symbols with prime). Eventually, similar calculations for some derivatives of all these systems have also been performed. Letter ’B’ (or ’b’) has been used if the −SiMe2H group has been substituted by −SiH3, ’C’ (or ’c’) if 9−BBN has been substituted by −BMe2, and ’D’ (or ’d’) if 9−BBN has been substituted by −BH2 (see Fig. 5).

Fig. 5
figure 5

Symbols introduced for the considered molecules

Full size image

Similar as for 1A, 2A, 3A and 4A, partially rather than fully optimized open forms have been used for estimations of interaction energies of H ⋯ B contacts in the closed forms. For the reasoning of their use, see the ’Energy of an intramolecular interaction’ section and discussion of results. Structures of fully optimized forms of all investigated systems as well as their open forms used as references for the interaction energy estimates are shown in Fig. 6.

Fig. 6
figure 6

Fully optimized closed and partially optimized open forms of investigated molecules

Full size image

Results and discussion

Discussed values of most important geometric parameters relating to the HSiCCB quasi-ring in open and closed forms of investigated systems are gathered in Table 1.

Table 1 Values of most important geometric parameters relating to the HSiCCB quasi-ring (bond distances in Å, angles and P in degrees), harmonic stretching vibration frequency of Si–H (in cm−1), estimated value of the interaction energy of the H ⋯ B contact (in kcal/mol)
Full size table

Local deformations of structure are determined by parameters P, \(\theta _{\text {HSiCC}}^{\text {def}}\), \(\theta _{\text {HSiCSi}}^{\text {def}}\) and θ SiCCB, where P, that can be called as pyramidalization parameter [25] of the trigonal boryl subunit, is just a difference between the round angle and the sum of all E1-B-E2 (where E1 and E2 is C or H) angles in this subunit, \(\theta _{\text {HSiCC}}^{\text {def}}\) and \(\theta _{\text {HSiCSi}}^{\text {def}}\) are deformation angles showing positional deviation of the H atom from the plane (for closed forms: \(\theta _{\text {HSiCC}}^{\text {def}} = \theta _{\text {HSiCC}}\) and \(\theta _{\text {HSiCSi}}^{\text {def}} = 180^{\circ } - \theta _{\text {HSiCSi}}\), for open forms: \(\theta _{\text {HSiCC}}^{\text {def}} = 180^{\circ } - |\theta _{\text {HSiCC}}|\) and \(\theta _{\text {HSiCSi}}^{\text {def}} = |\theta _{\text {HSiCSi}}|\)), and θ SiCCB is just the Si–C–C–B dihedral angle. Since in all primed systems, the θ HSiCC angle has been taken as 180° and then kept constant, the value of 0° for \(\theta _{\text {HSiCC}}^{\text {def}}\) for all these systems is a direct consequence of partial geometry optimization.

General features of closed forms

We begin analysis of our results shown in Table 1 on changes taking place upon the open form → closed form transformation, i.e when the Si–H ⋯ B bridge is formed. It is clearly seen that formation of this bridge leads to shorter Si ⋯B distances and longer Si–H bonds. Elongations of Si–H are accompanied by red-shifts of ν SiH. Moreover, more significant pyramidalization of the boryl fragment is observed as well. All these effects are geometrical evidences of bonding character of H ⋯ B contacts in the closed forms. This result is then confirmed by negative values of interaction energies. Only in case of nB (n = 1–4) systems the bonding character of H ⋯ B may be uncertain if one takes into account that the error of the open-closed method may be of the order of some 1–2 kcal/mol. Clearly, however, the bonding character of the SiH ⋯ B bridge is considerably weakened if the −SiMe2H group is substituted by the −SiH3 one. Conversely, compared to −SiH3, the −SiMe2H group leads to stronger H ⋯ B interaction. This most likely is due to the electron-donating properties of the methyl group.

1-Silacyclopent-2-enes vs 1-silacyclohex-2-enes

The main purpose of this article is to assess the strength of Si–H ⋯ B bridges in 1-silacyclopent-2-enes and to compare them to those obtained for similar 1-silacyclohex-2-enes (Fig. 1). As already mentioned in the ’Introduction’ section, on the basis of NMR spectroscopic data, Wrackmeyer et al. [4] have concluded that in the former group, the Si–H ⋯ B bridges are either absent or extremely weak, whereas, in the latter, Si–H ⋯ B bridges have been said to exist.

Our estimation of the interaction energy of the Si–H ⋯ B bridge in 1A \(_{\exp }\) gave −6.6 kcal/mol—quite large value considering, e.g. relatively long H ⋯ B distance (2.647 Å), acute α SiHB angle (103.4°) and relatively high value of ν SiH (2083 cm−1) comparing to 3A \(_{\exp }\) (1919 cm−1) where Si–H ⋯ B was said to exist [4]. So high (absolute) value results, however, from experimental values of geometric parameters that do not correspond to fully optimized ones. Considerably lower values of d Si⋯B (3.224 Å), d H⋯B (2.647 Å) and d SiH (1.325 Å) in 1A \(_{\exp }\) comparing to similar values in fully optimized 1A (3.276, 2.712 and 1.504 Å, respectively; Table 1) suggest significant packing forces in the former. Importantly, the full geometry optimization of 1A \(_{\exp }\) leads to modest lowering of its total energy than of 1a \(_{\exp }\). As a consequence, the energy of the H ⋯ B contact in the fully optimized 1A is much lower, amounting to −2.6 kcal/mol only. This value is even lower in 2A and amounts to −1.7 kcal/mol. Thus, if the H ⋯ B contacts in 1A and 2A are binding, they are indeed very weak as noted by Wrackmeyer et al. [4]. At this point, it is noteworthy that similar estimates for 3A and 4A have given energies of −5.1 and −3.9 kcal/mol, respectively (Table 1). Thus, the stabilizing character of the H ⋯ B contacts in both these systems is rather doubtless. This conclusion is in line with earlier spectroscopic results and the fact that, as we have shown in Fig. 7, the H ⋯ B interactions in both these systems are traced by corresponding bond paths, whereas similar bond paths are absent in case of the former two molecules, i.e. 1A and 2A.

Fig. 7
figure 7

Molecular graphs of 1A, 2A, 3A and 4A. Note H ⋯ B bond paths (indicated by blue arrow) in the latter two molecules

Full size image

As Bader has stated, the presence of a bond path (on a molecular graph) and a concomitant bond critical point indicate stabilizing interaction [33, 34]. On the other hand, however, a presumably binding interaction is not necessarily traced by a bond path [60, 61]. As already discussed in the earlier subsection, apart from negative values of interaction energies, changes of geometrical parameters also indicate stabilizing character of H ⋯ B contacts in 1A and 2A.

Electronic and steric effects

We have already shown that either clearly or presumably binding character of H ⋯ B contacts in 3A and 4A or 1A and 2A, respectively, results from highly electrodonor properties of methyl groups present in −SiMe2H. If they are substituted by hydrogens then the H ⋯ B contacts become hardly binding (ΔE int amounts to ca. −0.5 kcal/mol only for all systems nB; n = 1-4). On the contrary, Si ⋯B and H ⋯ B distances become much longer and the Si–H bond becomes much shorter. Also, the α SiHB angle becomes more acute (and close to the right angle) indicating that Si–H and C–B bonds are almost parallel to each other (see also Fig. 6). Another evidence of much weaker interactions in nB comparing to nA are higher values of ν SiH in the former. All these effects are particularly evident in respective pairs of 1-silacyclohex-2-enes.

It should be mentioned that the bulky 9-BBN group in nA and nB is not completely advantageous in our estimations of ΔE int in these systems because of possible H ⋯H repulsions in their na’ and nb’ open forms (Fig. 6). For this reason, we suspect that values of ΔE int obtained for these systems may be somewhat overestimated (Fig. 4). Nevertheless, both qualitative results as well as relations among computed values should be proper since the same structural changes, and thus, interatomic interactions occur in all pairs of open and closed forms. Moreover, all (9-BBN)H ⋯H(SiMe2H) or (9-BBN)H ⋯H(SiH3) distances are longer than ca. 2.15 or 2.42 Å found in 4a’ and 4b’, respectively, suggesting that repulsions are rather negligible as being no larger than ca. 0.5 kcal/mol (MP2/aug-cc-pVTZ) [31].

To eliminate the bulky 9-BBN group, we have considered nC systems possessing the -BMe2 group in place of 9-BBN (Fig. 5). Although this small group should reduce H ⋯H repulsions in open nc’ forms (the shortest H ⋯H distances are ca. 2.4 Å in 1c’ and 4c’ and ca. 2.5 Å in 2c’ and 3c’), on the other hand, it should lead to weaker Si–H ⋯ B bridges due to certain electron density shift from both methyl groups of −BMe2 to the formally empty 2p orbital on B. Indeed, in the case of both 1-silacyclohex-2-enes, the interaction energy decreases from −5.1 kcal/mol in 3A to −4.1 kcal/mol in 3C and from −3.9 kcal/mol in 4A to −3.0 kcal/mol in 4C (Table 1). Weakening of the relevant H ⋯ B interactions is also reflected in lower values of electron density at bond critical points of these interactions (ρ b). They amount to 0.063 and 0.055 au in 3A and 3C, respectively, whereas 0.060 and 0.053 au in 4A and 4C, respectively. In addition to the electron density, also, the delocalization index [62, 63] of H and B atoms (which is a measure of the number of electron pairs shared by these two atomic basins), DI(H,B), decreases as expected (from 0.206 au in 3A to 0.183 au in 3C and from 0.198 au in 4A to 0.175 au in 4C). Larger values of both ρ b and DI(H,B) in the former pair of molecules also indicate that H ⋯ B interactions should be stronger in 3A and 3C than in 4A and 4C. This suggestion is in line with our estimates of ΔE int. Similar decreases of ΔE int are, however, not observed for both 1-silacyclopent-2-enes, for which ΔE int is either the same (1A → 1C; ΔE int = −2.6 kcal/mol) or slightly increases (from −1.7 kcal/mol in 2A to −2.1 kcal/mol in 2C). This indicates that our estimates of ΔE int are more reliable for 1-silacyclohex-2-enes than those for 1-silacyclopent-2-enes and may most likely result from considerably higher values of ΔE int for the former group of systems.

In turn, to eliminate the electron donating properties of methyl groups in −BMe2, we have also investigated systems nD (and nd’) possessing −BH2 in place of −BMe2 (Fig. 5). Moreover, this substitution further reduces H ⋯H interactions in open reference forms. On the other hand, however, the −BH2 group is prone to rotate around the C–B bond (going in plane) so as to possibly form dihydrogen bond and to conjugate with the C=C bond of the ring. For this reason, the open reference nd’ systems have been obtained by freezing not only θ HSiCC (at 180°) but θ HBCC as well (at ±90°). Thus, −BH2 in nd’ was kept perpendicularly to the BCC plane. Since the nD systems feature rather significant pyramidalization of the −BH2 fragment (P amounts to ca. 10° in 1D and 2D and ca. 11° in 3D and 4D; Table 1), the pyramidalization energy, i.e. the energy that is needed to deform flat −BH2 group in nd’ to its somewhat pyramidal shape in nD, is included in our estimates of ΔE int. As discussed in the ’Energy of an intramolecular interaction’ section, this and other (small) deformations are, however, consequences of the H ⋯ B interactions in the nD closed forms. As expected, one obtains considerably high values of ΔE int. In 1D and 2D 1-silacyclopent-2-enes, they have been estimated as ca. −10 kcal/mol, whereas in both 1-silacyclohex-2-enes, ΔE int are higher amounting to −13.8 kcal/mol in 3D and −12.6 kcal/mol in 4D. So high values of ΔE int are in line with relatively large values of ρ b (ca. 0.08 au for all nD systems). It is noteworthy that among all 1L and 2L (L = A-D) only 1D and 2D feature a H ⋯ B bond path. Moreover, also, DI(H,B) values are rather high (0.291 au for 1D and 2D and 0.297 au for 3D and 4D). The characteristic feature of these systems is that d SiH > d H⋯B (Table 1), indicating a highly advanced transfer of H toward B. Similar effect has also been reported [18] in H3SiH ⋯BH3 (better written as H3Si ⋯H2⋅BH2). Interestingly, reported binding energy of this dimer amounts to -11.7 kcal/mol (MP2/aug-cc-pVTZ) [18]—closely to our estimates for nD.

Conclusions

The main purpose of this article is to assess strengths of H ⋯ B contacts in some 1-silacyclopent-2-enes and 1-silacyclohex-2-enes investigated earlier by Wrackmeyer et al. [4]. For this purpose, we have computed interaction energies of these contacts utilizing so-called open-closed method. In full agreement with previous conclusions based on NMR spectroscopic data [4], we have shown that the H ⋯ B contacts in investigated 1-silacyclohex-2-enes are indeed strong, whereas those in 1-silacyclopent-2-enes are much weaker. This result is supported by appropriate changes of geometrical parameters that take place upon the open form → closed form transformation and by reported values of some QTAIM-based parameters.

Influence of both the electronic and steric effects originating from the presence of specific substituents on the strength of relevant H ⋯ B contacts is discussed in detail. We have shown that relatively strong H ⋯ B interactions found in both 1-silacyclopent-2-enes and 1-silacyclohex-2-enes result from the presence of two methyl groups in −SiMe2H. If they are substituted by hydrogens, then H ⋯ B interactions become hardly bonding. On the other hand, if the 9-BBN group is subsituted by −BH2, then the investigated Si–H ⋯ B bridges feature many of the characteristic effects attesting to their considerable strength as also shown by high values of interaction energies and QTAIM-based parameters.

Some problems and ideas associated with the use of the open-closed method are discussed in detail. In particular, we have paid attention to the correct choice of the reference open system. It has been shown that utilization of the partial geometry optimization of the reference open system leads to reliable results.