Skip to main content
SpringerLink
Log in

Stacking Sequence Effect on the Fracture Behavior of Narrow L-Shaped Cross-Ply Laminates: Experimental Study

  • Published:
Strength of Materials Aims and scope

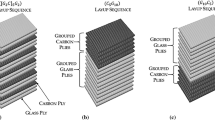
The stacking sequence effect of narrow L-shaped laminates on the fracture mode was studied. Two laminate stacking sequences were designed to analyze different fracture modes. The sequence layup J, i.e., [0/904/02/902/02/902/02/90]s trends to highlight the matrix fracture mode, whereas the stacking sequence layup I, i.e., [04/90/03/90/02/902/02/90]s tends to highlight the delamination mode. Load–deflection curves and fracture modes for these stacking sequences under a four-point bending loads were recorded and compared with the plane-strain empirical formula and experimental results. The results show that the stacking sequence has a significant effect on the initial fracture mode of narrow L-shaped laminar composites. Layup J shows matrix-dominant initial fracture due to the weak resistance of inner 90° plies to tangential tensile stresses, whereas layup I experiences delamination-dominant initial failure. The edge effect has a great influence on the fracture mode of layup J-like specimens, whereas it is very weak for layup I-like ones. The stacking sequence also influences the carrying capacity; a maximum fracture load of layup J is apparently lower than that of layup I, by about 23%.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.

Similar content being viewed by others

References

  1. B. Gozluklu, I. Uyar, and D. Coker, “Intersonic delamination in curved thick composite laminates under quasi-static loading,” Mech. Mater., 80, 163–182 (2015).

    Article  Google Scholar 

  2. R. H. Martin and W. C. Jackson, Damage Prediction in Cross-Plied Curved Composite Laminates, Technical Report NASA-TM-104089 (1991).

    Google Scholar 

  3. C. Thurnherr, R. M. J. Groh, P. Ermanni, and P. M. Weaver, “Investigation of failure initiation in curved composite laminates using a higher-order beam model,” Compos. Struct., 168, 143–152 (2017).

    Article  Google Scholar 

  4. M. H. Hassan, A. R. Othman, and S. Kamaruddin, “A review on the manufacturing defects of complex-shaped laminate in aircraft composite structures,” Int. J. Adv. Manuf. Tech., 91, 4081–4094 (2017).

    Article  Google Scholar 

  5. M. H. Hassan and A. R. Othman, “Contribution of processing parameters on void content in the vacuum bagging configurations of L-shaped composite laminates,” Int. J. Adv. Manuf. Tech., 93, 1333–1345 (2017).

    Article  Google Scholar 

  6. F. Georgiades, “Nonlinear equations of motion of L-shaped beam structures,” Eur. J. Mech. - A/Solid., 65, 91–122 (2017).

    Article  Google Scholar 

  7. M. Fiorina, A. Seman, B. Castanie, et al., “Spring-in prediction for carbon/epoxy aerospace composite structure,” Compos. Struct., 168, 739–745 (2017).

    Article  Google Scholar 

  8. C. Bellini, L. Sorrentino, W. Polini, and A. Corrado, “Spring-in analysis of CFRP thin laminates: numerical and experimental results,” Compos. Struct., 173, 17–24 (2017).

    Article  Google Scholar 

  9. Y. Shi and C. Soutis, “Modelling transverse matrix cracking and splitting of cross-ply composite laminates under four point bending,” Theor. Appl. Fract. Mec., 83, 73–81 (2016).

    Article  Google Scholar 

  10. S. Jimenez and R. Duddu, “On the parametric sensitivity of cohesive zone models for high-cycle fatigue delamination of composites,” Int. J. Solids Struct., 82, 111–124 (2016).

    Article  Google Scholar 

  11. C. T. Sun and S. R. Kelly, “Failure in composite angle structures Part I: Initial failure,” J. Reinf. Plast. Comp., 7, 220–232 (1988).

    Article  Google Scholar 

  12. S. Feih and H. R. Shercliff, “Composite failure prediction of single-L joint structures under bending,” Compos. Part A - Appl. S., 36, 381–395 (2005).

    Article  Google Scholar 

  13. M. R. Wisnom, “3-D finite element analysis of curved beams in bending,” J. Compos. Mater., 30, 1178–1190 (1996).

    Article  Google Scholar 

  14. ASTM D6415/D6415M. Standard Test Method for Measuring the Curved Beam Strength of a Fiber-Reinforced Polymer-Matrix Composite, ASTM International, West Conshohocken, PA (2006).

    Google Scholar 

  15. G. Wimmer, W. Kitzmüller, G. Pinter, et al., “Computational and experimental investigation of delamination in L-shaped laminated composite components,” Eng. Fract. Mech., 76, 2810–2820 (2009).

    Article  Google Scholar 

  16. S. Lekhnitskii, Theory of Elasticity of an Anisotropic Elastic Body, Mir, Moscow (1981).

    Google Scholar 

  17. C. T. Sun and S. R. Kelly, “Failure in composite angle structures Part II: Onset of delamination,” J. Reinf. Plast. Comp., 7, 233–244 (1988).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Materials Synthesis and Processing, Wuhan University of Technology, Wuhan, China

    Z. Y. Pan, S. X. Li & D. F. Cao

  2. Department of Civil and Structural College, Wuhan Huaxia University of Technology, Wuhan, China

    Z. Y. Pan

  3. School of Science, Wuhan University of Technology, Wuhan, China

    Q. F. Duan & Y. C. Zhong

Authors
  1. Z. Y. Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Q. F. Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. C. Zhong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. S. X. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. F. Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. F. Cao.

Additional information

Translated from Problemy Prochnosti, No. 1, pp. 223 – 230, January – February, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pan, Z.Y., Duan, Q.F., Zhong, Y.C. et al. Stacking Sequence Effect on the Fracture Behavior of Narrow L-Shaped Cross-Ply Laminates: Experimental Study. Strength Mater 50, 203–210 (2018). https://doi.org/10.1007/s11223-018-9960-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11223-018-9960-2

Keywords

Search

Navigation