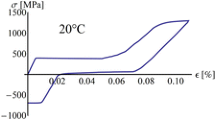
Shape instability belongs to one of significant types of violation for disposable structural elements under high-stress levels. Due to lack of fundamental data on materials, it is quite problematic to consider the shape instability in the design of disposable structural elements. The crystal plastic finite element method is proposed to investigate the dispersion of shape instability life data. It allows these data to be obtained from traditional material parameters. The shape instability behavior is described with the constitutive crystal model of plastic damage accumulation. Then, to improve the accuracy of life prediction, the new method is developed to construct the simulation model of true microstructure. A modeling algorithm based on the image processing technology is provided to reduce the virtual stresses from the transient crystal plastic modeling method. Comparison of experimental and predicted results shows good agreement at high stresses close to the elastic limit of the material.




Similar content being viewed by others
References
Y. F. Li, X. D. Pan, and G. L. Wang, “Low cycle fatigue and ratcheting properties of steel 40Cr under stress controlled tests,” Int. J. Fatigue, 55, 74–80 (2013).
S. J Park, K. S. Kim, and H. S. Kim, “Ratcheting behavior and mean stress considerations in uniaxial low-cycle fatigue of Inconel 718 at 649°C,” Fatigue Fract. Eng. Mater. Struct., 30, No. 11, 1076–1083 (2007).
C. B. Lim, K. S. Kim, and J. B. Seong, “Ratcheting and fatigue behavior of a copper alloy under uniaxial cyclic loading with mean stress,” Int. J. Fatigue, 31, No. 3, 501–507 (2009).
G. Z. Kang, Y. J. Liu, J. Ding, and Q. Gao, “Uniaxial ratcheting and fatigue failure of tempered 42CrMo steel: Damage evolution and damage-coupled viscoplastic constitutive model,” Int. J. Plasticity, 25, No. 5, 838–860 (2009).
H. Lim, J. D. Carroll, C. C. Battaile, et al., “Grain-scale experimental validation of crystal plasticity finite element simulations of tantalum oligocrystals,” Int. J. Plasticity, 60, 1–18 (2014).
D. Yu, K. An, Y. Chen, and X. Chen, “Revealing the cyclic hardening mechanism of an austenitic stainless steel by real-time in situ neutron diffraction,” Scripta Mater., 89, 45–48 (2014).
S. Keshavarz and S. Ghosh, “Multi-scale crystal plasticity finite element model approach to modeling nickel-based superalloys,” Acta Mater., 61, No. 17, 6549–6591 (2013).
M. Naderi, S. H. Hoseini, and M. M. Khonsari, “Probabilistic simulation of fatigue damage and life scatter of metallic components,” Int. J. Plasticity, 43, 101–115 (2013).
S. Ghosh and M. Anahid, “Homogenized constitutive and fatigue nucleation models from crystal plasticity FE simulations of Ti alloys, Part 1: Macroscopic anisotropic yield function,” Int. J. Plasticity, 47, 182–201 (2013).
Y. Liu and D. Chen, “Measurement of material mechanical properties using nano-indentation and finite element simulation,” J. Wuhan Univ. Technol., 27, 690–693 (2003).
C. O. Frederick and P. J. Armstrong, A Mathematical representation of the Multiaxial Bauschinger Effect, Report RD/B/N 731, Central Electricity Generating Board (1966).
N. Ohno and J.-D. Wang, “Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior,” Int. J. Plasticity, 9, No. 3, 375–390 (1993).
N. Ohno and J.-D. Wang, “Kinematic hardening rules with critical state of dynamic recovery, part II: Application to experiments of ratchetting behavior,” Int. J. Plasticity, 9, No. 3, 391–403 (1993).
J. Lemaitre and J.-L. Chaboche, Mechanics of Solid Materials, Cambridge University Press, Cambridge, UK (1990).
Y. F. Li, X. D. Pan, G. C. Wu, and G. L. Wang, “Shape-instability life scatter prediction of 40Cr steel: Damage-coupled crystal plastic probabilistic finite element method,” Int. J. Plasticity, 79, 1–18 (2016).
G. C. Wu, Y. F. Li, X. D. Pan, and G. L. Wang, “Numerical simulation of fatigue damage and shape instability behavior of steel 40Cr by the damage-coupled crystal plastic model,” Strength Mater., 49, No. 1, 118–124 (2017).
N. Ohno, “Constitutive modeling of cyclic plasticity with emphasis on ratcheting,” Int. J. Mech. Sci., 40, Nos. 2–3, 251–261 (1998).
N. Ohno, M. Abdel-Karim, M. Kobayashi, and T. Igari, “Ratchetting characteristics of 316FR steel at high temperature, part I: Strain-controlled ratchetting experiments and simulations,” Int. J. Plasticity, 14, Nos. 4–5, 355–372 (1998).
N. Ohno and M. Abdel-Karim, “Uniaxial ratchetting of 316FR steel at room temperature – II: Constitutive modeling and simulation,” J. Eng. Mater. Technol., 122, No. 1, 35–41 (2000).
Acknowledgments
National Natural Science Foundation of China (51405101), the research and innovation fund of Harbin Institute of Technology (Grant Number HIT.NSRIF.2015 053), the China Postdoctoral Science Foundation (Grant Numbers 2014M561340 and 2016T90277) and Heilongjiang Postdoctoral Fund (Grant Number LBH-Z14100).
Author information
Authors and Affiliations
Additional information
Translated from Problemy Prochnosti, No. 1, pp. 56 – 63, January – February, 2018.
Rights and permissions
About this article
Cite this article
Wu, G.C., Li, Y.F. & Wang, G.L. Probabilistic Simulation of Shape Instability Based on the True Microstructure Model. Strength Mater 50, 47–53 (2018). https://doi.org/10.1007/s11223-018-9941-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11223-018-9941-5