Abstract
We study the differentiability of mappings in the geometry of Carnot-Carathéodory spaces under the condition of minimal smoothness of vector fields. We introduce a new concept of hc-differentiability and prove the hc-differentiability of Lipschitz mappings of Carnot-Carathéodory spaces (a generalization of Rademacher’s theorem) and a generalization of Stepanov’s theorem. As a consequence, we obtain the hc-differentiability almost everywhere of the quasiconformal mappings of Carnot-Carathéodory spaces. We establish the hc-differentiability of rectifiable curves by way of proof. Moreover, the paper contains a new proof of the functorial property of the correspondence “a local basis ↦ the nilpotent tangent cone.”
Similar content being viewed by others
References
Goodman R. W., Nilpotent Lie Groups: Structure and Applications to Analysis, Springer-Verlag, Berlin (1970) (Lecture Notes in Math.; Vol. 562).
Rothschild L. and Stein E., “Hypoelliptic differential operators and nilpotent groups,” Acta Math., 137, 247–320 (1976).
Metivier G., “Fonction spectrale et valeurs proposes d’une classe d’operateurs,” Comm. Partial Differential Equations, 1, 479–519 (1976).
Nagel A., Stein E. M., and Wainger S., “Balls and metrics defined by vector fields. I: Basic properties,” Acta Math., 155, 103–147 (1985).
Vershik A. M. and Gershkovich V. Ya., “Nonholonomic dynamical systems, geometry of distributions and variational problems,” in: Dynamical Systems. VII. Encycl. Math. Sci. Vol. 16, 1994, pp. 1–81.
Gromov M., “Carnot-Carathéodory spaces seen from within,” in: Sub-Riemannian Geometry, Birkhäuser, Basel, 1996, pp. 79–323.
Pansu P., “Métriques de Carnot-Carathéodory et quasiisométries des espaces symétriques de rang un,” Ann. Math. (2), 129, No. 1, 1–60 (1989).
Vodopyanov S. K., “
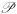 -Differentiability on Carnot groups in different topologies and related topics,” in: Studies on Analysis and Geometry, Sobolev Institute, Novosibirsk, 2000, pp. 603–670.
-Differentiability on Carnot groups in different topologies and related topics,” in: Studies on Analysis and Geometry, Sobolev Institute, Novosibirsk, 2000, pp. 603–670.Vodopyanov S. K. and Ukhlov A. D., “Approximately differentiable transformations and change of variables on nilpotent groups,” Siberian Math. J., 37, No. 1, 62–78 (1996).
Magnani V., “Differentiability and area formulas on stratified Lie groups,” Houston J. Math., 27, No. 2, 297–323 (2001).
Rademacher H., “Ueber partielle und totale Differenzierbarkeit. I,” Math. Ann., Bd 79, 340–359 (1919).
Stepanoff W., “Ueber totale Differenzierbarkeit,” Math. Ann., Bd 90, 318–320 (1923).
Folland G. B. and Stein E. M., Hardy Spaces on Homogeneous Groups, Princeton Univ. Press, Princeton (1982) (Math. Notes, Vol. 28).
Vodopyanov S. K. and Karmanova M. B., “Local geometry of Carnot manifolds under minimal smoothness,” Dokl. Akad. Nauk, 413, No. 3, 305–311 (2007).
Vodopyanov S. K. and Karmanova M. B., “Subriemannian geometry under minimal smoothness of vector fields,” Dokl. Akad. Nauk (2007) (to appear).
Karmanova M. and Vodopyanov S., Geometry of Carnot Manifolds Under Minimal Smoothness [Preprint, No. 183], Sobolev Institute, Novosibirsk (2006).
Vodopyanov S. K., “Differentiability of curves in the category of Carnot manifolds,” Doklady Math., 74, No. 2, 686–691 (2006).
Vodopyanov S. K., “Differentiability of mappings of Carnot manifolds and an isomorphism of tangent cones,” Dokl. Akad. Nauk, 411, No. 4, 439–443 (2006).
Vodopyanov S. K. and Greshnov A. V., “On the differentiability of mappings of Carnot-Carathéodory spaces,” Doklady Math., 67, No. 2, 246–251 (2003).
Vodopyanov S. K., “Geometry of Carnot-Carathéodory spaces and differentiability of mappings,” in: The Interaction of Analysis and Geometry, Amer. Math. Soc., Providence, RI, 2007, pp. 247–302 (Contemp. Math.; Vol. 424).
Vodopyanov S., Differentiability of Sobolev Mappings of Carnot-Carathéodory Spaces [Preprint, No. 182], Sobolev Institute, Novosibirsk (2006).
Hörmander L., “Hypoelliptic second order differential equations,” Acta Math., 119, 147–171 (1967).
Helgason S., Differential Geometry and Symmetric Spaces, Academic Press, New York; London (1962) (Pure Appl. Math.; Vol. 12).
Belläiche A., “The tangent space in sub-Riemannian geometry,” in: Sub-Riemannian Geometry, Birkhäuser, Basel, 1996, pp. 1–78.
Montgomery R., A Tour of Subriemannian Geometries, Their Geodesics and Applications, Amer. Math. Soc., Providence, RI (2002).
Pontryagin L. S., Ordinary Differential Equations, Addison-Wesley Publishing Company, Reading, Mass. etc.; Pergamon Press, London; Paris (1962) (Adiwes Internat. Ser. in Math.).
Vodopyanov S. K. and Ukhlov A. D., “Set functions and their applications in the theory of Lebesgue and Sobolev spaces. I,” Siberian Adv. Math., 14, No. 4, 78–125 (2004).
Burago D., Burago Yu., and Ivanov S., A Course in Metric Geometry, Amer. Math. Soc., Providence, RI (2001).
Margulis G. A. and Mostow G. D., “The differential of a quasi-conformal mapping of a Carnot-Carathéodory space,” Geom. Funct. Anal., 5, No. 2, 402–433 (1995).
Mitchell J., “On Carnot-Carathéodory metrics,” J. Differential Geometry, 21, 35–45 (1985).
Vodopyanov S. K., “Sobolev classes and quasiconformal mappings on Carnot-Carathéodory spaces,” in: Geometry, Topology and Physics. Proc. of the First Brazil-USA Workshop held in Campinas, Brazil, June 30–July 7, 1996. Eds.: B. N. Apanasov, S. B. Bradlow, W. A. Rodrigues, Jr., K. K. Uhlenbeck, Walter de Gruyter & Co, Berlin; New York, 1997, pp. 301–316.
Margulis G. A. and Mostow G. D., “Some remarks on the definition of tangent cones in a Carnot-Carathéodory space,” J. Anal. Math., 80, 299–317 (2000).
Agrachev A. and Marigo A., “Nonholonomic tangent spaces: intrinsic construction and rigid dimensions,” Electron. Res. Announc. Amer. Math. Soc., 9, 111–120 (2003).
Greshnov A. V., “Metrics and tangent cones of uniformly regular Carnot-Carathéodory spaces,” Siberian Math. J., 47, No. 2, 209–238 (2006).
Author information
Authors and Affiliations
Additional information
Original Russian Text Copyright © 2007 Vodopyanov S. K.
__________
Translated from Sibirskiĭ Matematicheskiĭ Zhurnal, Vol. 48, No. 2, pp. 251–271, March–April, 2007.
Rights and permissions
About this article
Cite this article
Vodopyanov, S.K. Differentiability of mappings in the geometry of Carnot manifolds. Sib Math J 48, 197–213 (2007). https://doi.org/10.1007/s11202-007-0022-4
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s11202-007-0022-4



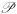 -Differentiability on Carnot groups in different topologies and related topics,” in: Studies on Analysis and Geometry, Sobolev Institute, Novosibirsk, 2000, pp. 603–670.
-Differentiability on Carnot groups in different topologies and related topics,” in: Studies on Analysis and Geometry, Sobolev Institute, Novosibirsk, 2000, pp. 603–670.