Skip to main content
SpringerLink
Log in

A short proof of rigidity of convex polytopes

  • Published:
Siberian Mathematical Journal Aims and scope Submit manuscript

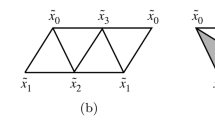
Abstract

We present a much simplified proof of Dehn’s theorem on the infinitesimal rigidity of convex polytopes. Our approach is based on the ideas of Trushkina [1] and Schramm [2].

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Trushkina V. I., “A coloring theorem and the rigidity of a convex polyhedron,” Ukrain. Geom. Sb., No. 24, 116–122 (1981).

  2. Schramm O., “How to cage an egg,” Invent. Math., 107, No. 3, 543–560 (1992). Available at http://dz-srv1.sub.unigoettingen.de/cache/toc/D183703.html.

    Article  MATH  MathSciNet  Google Scholar 

  3. Trushkina V. I., “Method of 3-coloring of graphs,” Siberian Math. J., 38, No. 2, 331–342 (1987).

    Article  Google Scholar 

  4. Connelly R., “Rigidity,” in: Handbook of Convex Geometry. Vol. A, North-Holland, Amsterdam, 1993, pp. 223–271.

    Google Scholar 

  5. Alexandrov A. D., Convex Polyhedra, Springer, Berlin (2005).

    Google Scholar 

  6. Berger M., Géométrie. Vol. 1–5, Nathan, Cedic, Paris (1977).

    Google Scholar 

  7. Dehn M., “Über die Starreit konvexer Polyeder,” Math. Ann., Bd 77, 466–473 (1916). Available at http://dz-srv1.sub.unigoettingen.de/cache/toc/D37460.html.

    Article  MATH  MathSciNet  Google Scholar 

  8. Whiteley W., “Rigidity and scene analysis,” in: Handbook of Discrete and Computational Geometry, CRC Press, Boca Raton, FL, 1997, pp. 893–916.

    Google Scholar 

  9. Alexandrov V., “Inverse function theorems and their applications to the theory of polyhedra, ” Rev. Math. Math. Phys. (to appear).

  10. Pak I., Lectures on Combinatorial Geometry and Convex Polytopes (a monograph in preparation).

  11. Fedorchuk M. and Pak I., “Rigidity and polynomial invariants of convex polytopes,” Duke Math. J., 129, 371–404 (2005). Available at http://www-math.mit.edu/∼pak.

    Article  MATH  MathSciNet  Google Scholar 

  12. Gluck H., “Almost all simply connected closed surfaces are rigid,” in: Lecture Notes in Math., Springer, Berlin, 438, 1975, pp. 225–239.

    Google Scholar 

  13. Roth B., “Rigid and flexible frameworks,” Amer. Math. Monthly, 88, No. 1, 6–21 (1981).

    Article  MATH  MathSciNet  Google Scholar 

  14. Whiteley W., “Infinitesimally rigid polyhedra. I. Statics of frameworks,” Trans. Amer. Math. Soc., 285, No. 2, 431–465 (1984).

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Massachusetts Institute of Technology, Cambridge, USA

    Igor Pak

Authors
  1. Igor Pak
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text Copyright © 2006 Pak Igor

__________

Translated from Sibirskiĭ Matematicheskiĭ Zhurnal, Vol. 47, No. 4, pp. 859–864, July–August, 2006.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pak, I. A short proof of rigidity of convex polytopes. Sib Math J 47, 710–713 (2006). https://doi.org/10.1007/s11202-006-0081-y

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11202-006-0081-y

Keywords

Search

Navigation