The entrepreneurship premium

Abstract

Recent evidence suggests that entrepreneurship does not pay enough to compensate people for the risk that it entails. It sometimes even shows an entrepreneurship discount. This paper shows that such a discount can arise if entrepreneurial skills and working skills are negatively correlated in the population of agents. The paper also shows that in an otherwise standard occupational choice setting, the entrepreneurship premium rises with entrepreneurial scarcity and falls with their span of control. Finally, liquidity constraints on startups raise the entrepreneurship premium by lowering the equilibrium wage.

1 Introduction

The findings of Hamilton (2000) and Moskowitz and Vissing-Jørgensen (2002) suggested that entrepreneurship does not pay enough to compensate for the risk that it entails. In spite of that, people enter and persist in business ownership and these authors conclude that the nonpecuniary benefits of self-employment are the main explanation.

Some recent empirical work on the topic has run counter to these initial findings. Kartashova (2014) argues that the results in Moskowitz and Vissing-Jogensen are not robust to the choice of sample period, and Astebro and Chen (2014) find a premium.

Some explanations given for the existence of a discount are that entrepreneurs (i) like risk (Kihlstrom and Laffont 1979), (ii) suffer from overoptimism (Kahneman and Lovallo 1993), (iii) derive utility, a nonpecuniary benefit from being self-employed (Hamilton 2000), (iv) underreport their earnings (Hurst et al. 2014; Sarada 2016), and (v) have outside options that are not properly measured (Vereshchagina and Hopenhayn 2009).

The explanation I give here is that when management and working abilities are negatively correlated, the premium can be negative. This is because then the median entrepreneur’s outside option is below the median wage. I show this in a simple version of the Roy (1951) model with two skills. Entrepreneurs can earn a discount when a large enough fraction of the population has the requisite managerial talent, and when the managerial span of control is high enough.

The model also implies that entrepreneurs will earn more when they are scarce and when they compete less with one another. I will argue that the entrepreneurship premium—essentially the ratio of profits to wages—depends on two parameters: It rises with the scarcity of entrepreneurial talent in the population, and falls with the managerial span of control—by the latter, we mean roughly optimal firm size.

This paper finds that paradoxically liquidity constraints raise the after tax premium by lowering the equilibrium wage. This effect is missing in Evans and Jovanovic (1989) and other models that take prices and wages as given. The model has no capital and the counterpart to the macroeconomic papers such as Bernanke et al. (1996) who have Cobb-Douglas production would be that if capital and labor were complements (elasticity of substitution less than 1), then a tightening of credit constraints would probably reduce the labor share.

Finally, profit taxes have no effect on the entrepreneurship premium because taxes reduce the demand for labor and wages fall in proportion. A similar result is in Boar and Midrigan (2019) who have a free entry condition for firms so taxing profits reduces the number of firms and reducing wages, which hurts the median worker.

2 Occupational choice

Here we are interested in entrepreneurship as one occupation and wage work as a second occupation. Most of the discussion will assume that these are the only two activities that people can engage in.

Roy (1951) discussed occupational selection when an individual embodied a vector of skills, with each component of the vector describing an occupation-specific ability. Roy did not provide a formal model. Lucas (1978) provided a model in which people differed in their management skill, but were perfect substitutes as workers. The wage that each worker received was endogenized, and the reward to managers was non-linear in managerial skill. The entrepreneur was the residual income recipient and his profit was a convex function of managerial talent.

Let us begin to outline the Roy-Lucas model assuming that labor is the only factor of production. The production function is

$$ q=xf\left( n\right) , $$

(1)

where n is employment and x is talent to manage. Managerial talent, x, is distributed according to the cumulative distribution function $G\left (x\right )$, with density $g\left (x\right )$. As workers, people are perfect substitutes, each supplying one unit of labor.

If type x were to choose to be an entrepreneur that manages the production, he would solve the problem

$$ \pi \left( x,w\right) =\max_{n}\left\{ xf\left( n\right) -wn\right\} $$

(2)

taking the wage w as given. The first-order condition is $xf^{\prime }\left (n\right ) =w$, from which we obtain the demand function for labor:

$$ n^{d}\left( x,w\right) =\left( f^{^{\prime }}\right)^{-1}\left( \frac{w}{x} \right) $$

(3)

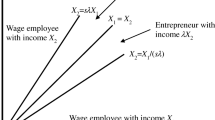
is increasing in x. Figure 1 illustrates a firm’s problem for two different values of x, i.e., x₁ and x₂, (where x₂ > x₁).

Fig. 1

Demand for labor by two different managers

Note that profits increase with x and they do so at an increasing rate: That is, π is convex in x: By the envelope theorem, $\frac {\partial }{ \partial x}\pi \left (x,w\right ) =f\left (n^{d}\right ) ,$ which itself increases with x because n^d does.

The set of managers

The marginal entrepreneur has a level of talent z such that he is indifferent between running a firm and being a worker:

$$ \pi \left( z,w\right) =w $$

(4)

The determination of z is illustrated in Fig. 2. People with x ≥ z are better off being managers. The rest are better off being workers. The person with x = z is indifferent.

Fig. 2

The determination of z

Market clearing

Supply of workers must equal the demand for them:

$$ G\left( z\right) ={\int}_{z}^{\infty }n^{d}\left( x,w\right) g\left( x\right) dx $$

(5)

Equilibrium is a pair of scalars $\left (w,z\right )$ such that Eqs. 3, 4, and 5 hold.

The entrepreneurship premium

The ratio of average entrepreneurial income to wage income is

$$ \frac{\bar{\pi}}{w}=\frac{1}{w}\frac{1}{1-G\left( z\right) }{\int}_{z}^{\infty }\pi \left( x,w\right) g\left( x\right) dx $$

(6)

In this simple model, this ratio must exceed unity. So must the ratio of median profits to wages,

$$ \frac{\pi_{\text{med}}}{w}=\frac{\pi \left( \hat{x}_{\text{med}},w\right) }{ w}. $$

(7)

where $\hat {x}_{\text {med}}$ is median entrepreneurial ability that satisfies

$$ \frac{G\left( \hat{x}_{\text{med}}\right) -G\left( z\right) }{1-G\left( z\right) }=\frac{1}{2}. $$

Once agents differ in x, the inframarginal entrepreneurs earn profits higher than w. This is seen in Fig. 2 where the smallest income, w, is earned by workers and all higher incomes are earned by entrepreneurs. This extreme conclusion hinges on the assumption that as worker agents are perfect substitutes.

Iso-elastic production function and a uniform distribution of x

For the rest of this section, we shall work with the following assumptions:

$$ f\left( n\right) =n^{\alpha }\text{, \ \ \ and \ \ }G\left( x\right) =x\text{ \ for \ }0\leq x,\alpha \leq 1\text{.} $$

Optimality of n states that the first-order condition xαn^α− 1 = w is met so that the demand function for labor is

$$ n^{d}\left( x,w\right) =\left( \frac{\alpha x}{w}\right)^{1/\left( 1-\alpha \right) } $$

(8)

Appendix Eq. 29 shows that the maximized profit function is

$$ \pi \left( x,w\right) =\left( 1-\alpha \right) \left( \frac{\alpha }{w} \right)^{\alpha /\left( 1-\alpha \right) }x^{1/\left( 1-\alpha \right) }. $$

(9)

This example has a single-free parameter, namely α, which determines the size of firms as measured by its employment, n^d. The following is proved in the Appendix:

Proposition 1

The solutions for the equilibrium $\left (z,w\right )$ are

$$ \begin{array}{@{}rcl@{}} z &=&\left( \frac{\alpha }{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }\text{ \ \ \ and \ \ \ } \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} w &=&\alpha^{\alpha }(1-\alpha )^{1-\alpha }z. \end{array} $$

(11)

and the entrepreneurship premium (6) in this case is

$$ \frac{\bar{\pi}}{w}=\frac{1}{\left( \left( \frac{2}{\alpha }\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }-1\right) }\frac{1-\alpha }{ \alpha }. $$

(12)

Figure 3 plots the premium, $\bar {\pi }/w,$ and shows it to be declining in α. Indeed, as $\alpha \rightarrow 1$, the fraction of workers, z, converges to one, and the fraction of managers, 1 − z, converges to zero.

Fig. 3

Plot of Eqs. 10, 11, and 12. The red curve is $\bar {\pi }=\omega$, blue curve is z, and the dashed curve is ω

The best managers can manage everything and yet the management premium is at its lowest level. L’Hopital’s rule shows that

$$ \lim\limits_{\alpha \rightarrow 1}\frac{\bar{\pi}}{w}=\frac{1}{\ln 2}=1.44,\text{ } \lim\limits_{\alpha \rightarrow 1}w=1\text{\ } $$

(13)

(see the Appendix).

Conversely, as $\alpha \rightarrow 0$, the premium goes to infinity as the fraction of workers converges to zero and

$$ \lim\limits_{\alpha \rightarrow 0}\frac{\bar{\pi}}{w}=+\infty $$

Mean vs. median premia

In this model, differences in x create a positive entrepreneurship premium. If all agents had the same x, then all would be indifferent between the two occupations; the ratios in Eqs. 6 and 7 would equal unity. Otherwise, the mean premium could be larger or smaller than the median depending on the distribution of x. In the uniform case, the mean premium must exceed the median because $\pi \left (x,w\right )$ is convex in x as shown in Fig. 2 and because x is uniformly distributed.

Evidently, this version of the model cannot generate a management discount at any percentile, median or any other. We shall, however, be able to generate it when we generalize the distribution of skills to allow for more heterogeneity in workers’ abilities.

The distribution of entrepreneurial talent

Among people who opted to be entrepreneurs the CDF of $x\in \left [ z,1\right ]$ is

$$ H\left( x\right) =\frac{x-z}{1-z}. $$

(14)

Given (14), we can use Eq. 8 to derive the distribution of employment and Eq. 9 to derive the distribution of profits, i.e., of entrepreneurial incomes.

The distribution of firm size

Given (14), and (11 ), the CDF of n is

$$ {\Phi} \left( n\right) =\frac{\frac{w}{\alpha }n^{1-\alpha }-z}{1-z},\text{ \ \ for \ \ }n\in \left[ \frac{\alpha }{1-\alpha },\frac{\alpha }{1-\alpha } z^{-1/\left( 1-\alpha \right) }\right] . $$

Using (10) and (11) to replace z and w, we obtain

$$ {\Phi} \left( n\right) =\frac{(\frac{1-\alpha }{\alpha })^{1-\alpha }n^{1-\alpha }-1}{\left( \frac{2}{\alpha }\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }-1},\text{ \ \ for \ \ }n\in \left[ \frac{\alpha }{ 1-\alpha },\frac{\alpha }{1-\alpha }\left( \frac{2}{\alpha }\right)^{1/\left( 2-\alpha \right) }\right] . $$

(15)

Thus, as α grows, the level and dispersion of n grow without bound, as shown in Figs. 4 and 5.

Fig. 4

Φ(n) for α below 0.9

Fig. 5

Φ(n) for α above 0.95

The distribution of entrepreneurial incomes

Surprisingly, the distribution of entrepreneurial incomes does not get much more dispersed as the span of control α grows. We show that this is so when x is uniformly distributed. Let maximized profits be s. That is, let

$$ \begin{array}{@{}rcl@{}} s &=&\pi \left( x,w\right) =Ax^{1/\left( 1-\alpha \right) },\text{ \ \ \ where} \\ A &=&\left( 1-\alpha \right) \left( \frac{\alpha }{w}\right)^{\alpha /\left( 1-\alpha \right) }. \end{array} $$

Given (14), the CDF with support $s\in \left [ w,A\right ]$ is

$$ {\Psi} \left( s\right) =\frac{\left( s/A\right)^{1-\alpha }-z}{1-z}. $$

The case $\alpha \rightarrow 0$

Then since $z\rightarrow 0$ as $\alpha \rightarrow 0$, s converges to the uniform distribution on $\left [ 0,1\right ]$. That is,¹

$$ \lim_{\alpha \rightarrow 0}{\Psi} \left( s,\alpha \right) =s\text{ for }s\in \left[ 0,1\right] . $$

(16)

The case α = 1/2

As the Appendix shows, the support of Ψ shrinks by a factor of about two when α = 1/2

$$ {\Psi} \left( s,\alpha =1/2\right) =\frac{s^{1/2}2^{1/6}-2^{-2/3}}{1-2^{-2/3}} \text{for }s\in \left[ 0.32,0.79\right] . $$

(17)

The case α = 1

The derivations are lengthy and they too are reported in Appendix 3. The resulting plots are shown in Figs. 6 and 7.

Fig. 6

Ψ(s) for α below 0.9

Fig. 7

Ψ(s) for α above 0.95

The support again widens as α approaches unity, as shown in Fig. 7.

Finally, Fig. 8 shows ${\sigma _{s}^{2}}$ as a function of α. As expected from the previous two plots of Ψ, the variance is a U-shaped function of α, attaining a minimum at α = 0.47.

Fig. 8

The effect of α on ${\sigma ^{2}_{s}}$ generated by the distribution Ψ(s)

3 Occupational choice when talent also differs among workers

It would seem reasonable that not only managerial skill but working skill differs among people. An obvious generalization to the model described above is to build a model that would allow for different levels of worker skill, as in Jovanovic (1994). I will briefly describe the model, and then in the next section, link the model to the question of the entrepreneurship premium.

Endow agents with a pair {x,y}, where x represents a person’s skill level as a manager and y is his skill level as a worker, no longer identical over workers. The pair of abilities is distributed according to the CDF F(x,y). Firms still produce output q as in Eq. 1, except that now n denotes not the number of workers but, rather, the total amount of efficiency units of skill that manager x employs. Manager x still solves the problem in Eq. 2 and leads to optimal demand for efficiency units in Eq. 3 where w is the wage per efficiency unit.

Occupational choice

Now potential wage earnings differ among people and instead of a single number, z, that we depicted in Fig. 2, we have an indifference curve in $\left (x,y\right )$ space. Now the skill type $\bar {y}\left (x\right )$ is indifferent between becoming a manager and a worker:

$$ \pi (x,w)=w\bar{y}\left( x\right) . $$

(18)

Instead of the region to the right of point z in Fig. 2, the set of managers is the following subset of the positive $\left (x,y\right )$ quadrant:

$$ \text{ Set of managers = M = }\left\{ \left( x,y\right) \mid \pi \left( x,w\right) >wy\right\} . $$

Instead of Eq. 5, the market-clearing condition says that the supply of efficiency units of labor must equal the demand for them:

$$ {\int}_{\mathbb{R}_{+}^{2}-M}ydF\left( x,y\right) ={\int}_{M}n^{d}\left( x,w\right) dF\left( x,y\right) . $$

(19)

We now show that $\bar {y}(x)$ is increasing and convex as shown Fig. 9.

Fig. 9

Heterogeneous labor skills. M is the southeast region

The next subsection discusses the case in which the distribution in $\left (x,y\right )$ space consists of just two points.

4 Negatively correlated $\left (x,y\right )$ and a possible entrepreneurship discount

In the model outlined above, one would expect x and y to be positively correlated in the population. But the opposite can also arise: A well-known example of this phenomenon is someone who can perform very well as a manager but, because he wants to make his own decisions and cannot easily take orders or be told what to do, makes a bad employee.

In Jovanovic (1982), I analyzed some implications of the case where x and y were negatively correlated. The implication I stressed was that which arises when abilities in entrepreneurship and wage work are unobserved. A form of favorable (instead of adverse) selection will result.

For our purposes, however, let us assume that for each person $\left (x,y\right )$ is common knowledge. Suppose that $F\left (x,y\right )$ has mass only at two points, $\left (0,1\right )$ and $\left (1,0\right )$ as follows:

$$ \left( x,y\right) =\left\{ \begin{array}{c} \left( 0,1\right) \text{ \ \ with prob. \ \ \ \ }N\text{ \ \ \ } \\ \left( 1,0\right) \text{ \ \ with prob. \ }1-N \end{array} \right. $$

where $N\in \left (0,1\right )$. Now each person is capable of performing only one task, one occupation, with the other occupation yielding a zero income.² As we shall see, in general, no one can be indifferent between the two occupations.

Measure of the scarcity of entrepreneurs

The parameter N measures the abundance of labor talent or equivalently, the scarcity of entrepreneurial talent. There will be 1 − N firms employing N workers, and employment in each firm is

$$ n=\frac{N}{1-N}. $$

The management premium will be increasing in N, not surprisingly.

The equilibrium wage

The problem of each firm is still as in Eq. 2, and the first-order condition is

$$ f^{\prime }\left( n\right) =w $$

(20)

Suppose that $f\left (n\right ) =n^{\alpha }$ where α < 1. Then Eq. 20 reads

$$ w=\alpha n^{\alpha -1} $$

(21)

and entrepreneurial income is

$$ \pi \!=n^{\alpha }\!-wn\!=\left( 1-\alpha \right) n^{\alpha }\!=\left( 1\!-\alpha \right) \left( \frac{N}{1-N}\right)^{\alpha } $$

(22)

The entrepreneurship premium

This version of the model can fit an entrepreneurship premium of any size. The ratio of entrepreneurial income to wage income is

$$ \frac{\pi }{w}=\frac{n^{\alpha }-wn}{w}=\frac{1-\alpha }{\alpha }\frac{N}{1-N }. $$

(23)

and therefore

$$ \frac{\pi }{w}\gtrless 1\Longleftrightarrow N\gtrless \alpha . $$

(24)

Since all entrepreneurs and all workers earn the same respective incomes, there is no distinction between the mean premium and the median premium.

Figure 10 plots the entrepreneurship premium in Eq. 23 for N = 0.25 (red curve), N = 0.5 (black curve), and N = 0.75 (blue curve). That the premium rises with N was to be expected. On the other hand, the span of managerial control, α, reduces the premium. We found the same result in Proposition 1 and it was portrayed by the top curve in Fig. 3 which, however, always exceeded unity. Now, however, the premium falls below 1 when N < α, as stated in Eq. 24. This may at first seem surprising because a high α measures ability for managers to control more workers, raising their marginal product in his firm. It has the same effect as would a rise in the ratio of managers to workers that a fall in N would represent. But the demand for entrepreneurs is inelastic in the model and the rise in α is similar to the case of “immiserizing productivity growth” that prevails in some other contexts.³

Fig. 10

The premium in Eq. 23 for $N = \frac {1}{4}$ (red), $\frac {1}{2}$ (black), $\frac {3}{4}$ (blue)

4.1 Liquidity constraints and the entrepreneurship premium

4.1.1 Liquidity constraints

In the above model, suppose an entrepreneur must pay wages in advance, and that he has wealth m

$$ wn\leq m $$

At equilibrium, w^equil. = αn^α− 1 ⇒ Liq. constraint is binding if HCode

$$ m<w^{\text{equil.}}n $$

i.e., if

$$ m<\alpha n^{\alpha } $$

(25)

If Eq. 25 is binding, to clear the market, the wage has to satisfy

$$ w=\frac{m}{n} $$

(26)

So, with a binding liquidity constraint so that Eq. 26 holds, the entrepreneurship premium is

$$ \frac{\pi }{w}=\frac{n^{\alpha }-wn}{w}=\frac{n^{1+\alpha }}{m}-n $$

where

$$ n=\frac{N}{1-N}. $$

Consider the example N = 1/2. In the absence of the liquidity constraint, Eq. 23 implies

$$ \frac{\pi }{w}=\frac{1-\alpha }{\alpha }, $$

and then the Liq. constraint binds if m < α, in which case

$$ \frac{\pi }{w}=\max \left( \frac{1-\alpha }{\alpha },\frac{1-m}{m}\right) . $$

Thus, the green curve is the relation when there is no liquidity constraint, or when m assumes any value exceeding unity.

Figure 11 plots the relation between α and π/w. In the figure, the downward sloping green curve shows relation when there is no liquidity constraint, and it obtains for any value of m ≥ 1. The rest of the lines have the following meaning:

$$ \begin{array}{lll} \text{Value of}\ m & \text{Curve color} \\ 1/4 & \text{Red} \\ 1/2 & \text{Black} \\ 3/4 & \text{Blue} \\ \geq 1 & \text{Green} \end{array} $$

Fig. 11

The case $N = \frac {1}{2}$ for $m = \frac {1}{4}$ (red), $\frac {1}{2}$ (black), $\frac {3}{4}$ (blue)

4.2 The effects of profit taxes

Suppose a τ is imposed on firms and rebated to all agents lump sum. To keep things simple, suppose that there are no taxes on wage earnings. Then the first-order condition (21) changes to

$$ w=\left( 1-\tau \right) \alpha n^{\alpha -1} $$

(27)

and then the entrepreneurship premium becomes

$$ \frac{\pi }{w}=\frac{\left( 1-\tau \right) \left( n^{\alpha }-wn\right) }{ \left( 1-\tau \right) \alpha n^{\alpha -1}}=\frac{\left( n^{\alpha }-\alpha n^{\alpha }\right) }{\alpha n^{\alpha -1}}=\frac{1-\alpha }{\alpha }\frac{N}{ 1-N}, $$

(28)

which does not depend on τ and which is the same as the expression in Eq. 23.

This static model cannot do justice to the effects of taxes on capital formation, on research, or other investments that take time to mature. Indeed, Braunerhjelm et al. (2019) analyze a modified version of the entrepreneurial choice model and show that taxes discourage entrepreneurial formation.

5 Discussion

By continuity, we expect the results to hold up if the assumptions are slightly modified. One could let the correlation of x and y be above negative unity by introducing some (1,1) types and $\left (0,0\right )$ types. For example, one can introduce some overoptimism by letting a positive fraction of agents be $\left (0,1\right )$ types while at the same time believing themselves to be $\left (1,1\right )$ types. Other issues that concern measurement and identification are the following:

Identifying inability vs. unwillingness to work for others

How do we disentangle a negative correlation of $\left (x,y\right )$ from a zero correlation coupled with a distaste for working for someone else? The question is about a negative correlation of potential earnings contrasted to a negative correlation of the nonpecuniary benefits. Cagetti and De Nardi (2006) assume a zero correlation between x and y and do not have a nonpecuniary benefit. One may need data from both accepted and rejected offers, to separate the two.

Rejected option information

Data on rejected offers would allow us to disentangle negative ability correlation from a distaste for working for others. If abilities are negatively correlated, the self-employed would have rejected wage offers that were below their entrepreneurial earnings. On the other hand, a self-employed person may reject a wage higher than his or her actual earnings, and such an action would signal a distaste for working for others. If one rejected a low w, that implies $Cov\left (x,y\right ) <0$. I discussed some implications of a negative covariance of talents in two occupations in Jovanovic (1982).

Evidence on $Cov\left (x,y\right )$

Evans and Jovanovic (1989) estimated a negative $Cov\left (x,\text { wealth}\right )$. If people accumulated their wealth while earning wages (i.e., for most people in the sample), then their wealth signals y. Perhaps people earned less because while working for others, they took time out to try to come up with a new idea. That finding would then be consistent with a negative correlation between x and y.

Some of the evidence on $Cov\left (x,y\right )$ is inconclusive. Table 4 of Hamilton (2000) contains some inconclusive evidence on $Cov\left (x,y\right )$; it estimates the effects of nine regressors in two regressions—one for self-employed earnings, the other for paid employment earnings. Five of the regressors’ coefficient estimates have the same sign in the two equations suggesting a positive covariance in the marginal distribution of $\left (x,y\right )$, four have opposite signs suggesting $Cov\left (x,y\right ) <0$. Similar results are in Table 2 of Humphries (2018). In a similar vein, Gendron-Carrier (2018) finds that people with a comparative advantage in entrepreneurship are equally likely to be found at both ends of the ability distribution.

Finally, some evidence points to a positive $Cov\left (x,y\right )$: Table S3 of Hincapié (2019) reports a positive correlation for most of the subgroups he considers, and Alvarez-Cuadrado et al. (2019) find that skills in agriculture and non-agricultural entrepreneurship are positively correlated.

6 Some questions for future research

The entrepreneurship premium clearly relates to the large macroeconomic literature on the financial acellerator, as well as on the literature on the financial barriers to development. What we call entrepreneurship covers a fairly broad array of activities. Often, that activity involves the management of a capital stock and the hiring of employees. But that is not always the case, especially in less developed economies where it sometimes resembles a form of disguised unemployment. Levine and Rubinstein (2018) introduce two types of entrepreneurship that differentiates between the traditional activities of entrepreneurs and that of other self-employed people, and this helps explain the data. Recently, Lindenlaub (2017) has analyzed sorting of jobs and workers in which types are multidimensional and this class of models can be extended to include occupational choice.

More can be done to model what entrepreneurs actually do. An entrepreneur exploits an opportunity he has come across, he providing a service or product possibly having some unique attributes as compared with the what others offer. And once the business is in place, what is a manager’s function, what role does the entrepreneur take on? Prescott and Visscher (1980) model an employer that screens employees so as to better assign them to tasks. Venezia (1985) and Jovanovic and Nyarko (1996) assume that the manager chooses the right input mix. Garicano (2000) assumes that the manager solves problems raised by his employees, and that the output of the firm is the sum of solved problems. Kihlstrom and Laffont (1979) assume that the manager’s role is to insure the workers against risk.

A related question is, how does—or how should—a prospective entrepreneur go about starting a business? Presumably some market research would help so that the product ends up being what the customer wants. A search for possible suppliers of inputs would also help. More models are needed to understand better this process. Rob (1991) models a group of established firms finding out about the demand for their product by gradually expanding capacity. Closer to analyzing the individual entrepreneur is a model by Allen (2014) in which entrants into a new market engage in sequential search to determine in which sub-market to sell their product—suitable markets being those where prices are high. One can imagine analyzing the search for an input supplier—suitable suppliers being those that ask for low prices or offer high quality. Such models would mirror the literature on gradual growth in awareness by customers about new products, such as Bass (1969) and Perla (2016).

Policy intervention is most likely needed in two areas. First, reducing the liquidity constraint deterrent to entrepreneurship, which relates to the ongoing work on misallocation, such as Midrigan and Xu (2014). Second, possibly speeding up the diffusion of knowledge without reducing the incentives to create it. A variety of instruments including research subsidies and patent protection should possibly be used and empirical results in Acs and Audretsch (1988), Acs et al. (1994), and others can provide a guide.

Finally, distinguishing nonpecuniary benefits from a negative skill correlation is a question of first-order policy importance. There is evidence that many startups are low-productivity.⁴ If these are people who are in the business because they derive utility from it, the case for providing financial assistance is weak. If, on the other hand, they would be even less productive as employees, it is easier to argue they deserve help.

Appendices

Appendix 1. Proof of Proposition 1

We start by deriving, for this example, the function $\pi \left (x,w\right )$ defined in Eq. 2. Using Eq. 8 we have

$$ \begin{array}{@{}rcl@{}} \pi \left( x,w\right) &=&x\left( n\right)^{\alpha }-wn=x\left( \frac{\alpha x}{w}\right)^{\alpha /\left( 1-\alpha \right) }-w\left( \frac{\alpha x}{w} \right)^{1/\left( 1-\alpha \right) } \\ &=&\left[ \left( \frac{\alpha }{w}\right)^{\alpha /\left( 1-\alpha \right) }-w\left( \frac{\alpha x}{w}\right)^{1/\left( 1-\alpha \right) }\right] x^{1/\left( 1-\alpha \right) } \\ \pi \left( x,w\right) &=&\left( 1-\alpha \right) \left( \frac{\alpha }{w} \right)^{\alpha /\left( 1-\alpha \right) }x^{1/\left( 1-\alpha \right) } \end{array} $$

(29)

The indifference condition (4) reads

$$ \left( 1-\alpha \right) \left( \frac{\alpha }{w}\right)^{\alpha /\left( 1-\alpha \right) }z^{1/\left( 1-\alpha \right) }=w, $$

(30)

i.e.,

$$ \left( 1-\alpha \right) \alpha^{\alpha /\left( 1-\alpha \right) }z^{1/\left( 1-\alpha \right) }=w^{1/\left( 1-\alpha \right) }, $$

because $1+\alpha /\left (1-\alpha \right ) =1/\left (1-\alpha \right )$. Therefore,

$$ \frac{w}{z}=\alpha^{\alpha }\left( 1-\alpha \right)^{1-\alpha }. $$

(31)

The market-clearing condition (5) reads

$$ \begin{array}{@{}rcl@{}} z &=&{{\int}_{z}^{1}}\left( \frac{\alpha x}{w}\right)^{1/\left( 1-\alpha \right) }dx \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} &=&\left. \frac{1}{1+\frac{1}{1-\alpha }}\left( \frac{\alpha }{w}\right)^{1/\left( 1-\alpha \right) }x^{1+1/\left( 1-\alpha \right) }\right\vert_{z}^{1} \\ &=&\left. \frac{1-\alpha }{2-\alpha }\left( \frac{\alpha }{w}\right)^{1/\left( 1-\alpha \right) }x^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right\vert_{z}^{1} \\ &=&\frac{1-\alpha }{2-\alpha }\left( \frac{\alpha }{w}\right)^{1/\left( 1-\alpha \right) }\left( 1-\left( z\right)^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right) \end{array} $$

(33)

From Eq. 30:

$$ z=\frac{w}{\alpha^{\alpha }(1-\alpha )^{1-\alpha }} $$

(34)

Solve (34) for w in terms of z and substituting into Eq. 33:

$$ w=z\alpha^{\alpha }(1-\alpha )^{1-\alpha } $$

i.e., Eq. 11.

Therefore,

$$ z=\frac{1-\alpha }{2-\alpha }\left( \frac{\alpha }{z\alpha^{\alpha }(1-\alpha )^{1-\alpha }}\right)^{1/\left( 1-\alpha \right) }\left( 1-z^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right). $$

That is, since

$$ \left( \frac{\alpha }{\alpha^{\alpha }(1-\alpha )^{1-\alpha }}\right)^{ \frac{1}{1-\alpha }}=\frac{\alpha }{1-\alpha }, $$

$$ z=\frac{1-\alpha }{2-\alpha }z^{-1/\left( 1-\alpha \right) }\frac{\alpha }{ 1-\alpha }\left( 1-\left( z\right)^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right) , $$

i.e.,

$$ z=\frac{1}{2-\alpha }\alpha \left( z^{-1/\left( 1-\alpha \right) }-z^{-1/\left( 1-\alpha \right) +\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right) =\frac{1}{2-\alpha }\alpha \left( z^{-1/\left( 1-\alpha \right) }-z\right) $$

i.e.,

$$ \begin{array}{@{}rcl@{}} z\left( 1+\frac{\alpha }{2-\alpha }\right) &=&\frac{1}{2-\alpha }\alpha z^{-1/\left( 1-\alpha \right) }\Longleftrightarrow \\ z\frac{2}{2-\alpha } &=&\frac{1}{2-\alpha }\alpha z^{-1/\left( 1-\alpha \right) }\Longleftrightarrow \\ 2z &=&\alpha z^{-1/\left( 1-\alpha \right) }\Longleftrightarrow \\ \frac{\alpha }{2} &=&z^{1+\frac{1}{1-\alpha }}=z^{\frac{2-\alpha }{1-\alpha }} \end{array} $$

which implies (10).

Finally we prove (12) Substituting into Eqs. 11 from 10.

$$ \begin{array}{@{}rcl@{}} w&=&\alpha^{\alpha }\left( 1-\alpha \right)^{1-\alpha }\left( \frac{\alpha }{ 2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right)}\\&=&\alpha^{\alpha +\left( 1-\alpha \right) /\left( 2-\alpha \right) }\left( 1-\alpha \right)^{1-\alpha }\left( \frac{1}{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }, \end{array} $$

The ratio of entrepreneur x’s earnings to the wage is (since $1+\alpha /\left (1-\alpha \right ) =1/\left (1-\alpha \right )$),

$$ \frac{\pi \left( x,w\right) }{w}=\left( 1-\alpha \right) \alpha^{\alpha /\left( 1-\alpha \right) }x^{1/\left( 1-\alpha \right) }w^{-1/\left( 1-\alpha \right) } $$

Now

$$ \left( \alpha^{\alpha +\left( 1-\alpha \right) /\left( 2-\alpha \right) }\left( 1-\alpha \right)^{1-\alpha }\left( \frac{1}{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }\right)^{1/\left( 1-\alpha \right) }=\alpha^{\alpha /\left( 1-\alpha \right) +1/\left( 2-\alpha \right) }\left( 1-\alpha \right) \left( \frac{1}{2}\right)^{1/\left( 2-\alpha \right) } $$

and so

$$ \begin{array}{@{}rcl@{}} \frac{\pi \left( x,w\right) }{w} &=&\frac{\left( 1-\alpha \right) \alpha^{\alpha /\left( 1-\alpha \right) }x^{1/\left( 1-\alpha \right) }}{\alpha^{\alpha /\left( 1-\alpha \right) +1/\left( 2-\alpha \right) }\left( 1-\alpha \right) \left( \frac{1}{2}\right)^{1/\left( 2-\alpha \right) }}= \frac{x^{1/\left( 1-\alpha \right) }}{\alpha^{1/\left( 2-\alpha \right) }\left( \frac{1}{2}\right)^{1/\left( 2-\alpha \right) }} \\ &=&\left( \frac{2}{\alpha }\right)^{1/\left( 2-\alpha \right) }x^{1/\left( 1-\alpha \right) } \end{array} $$

Since $1+1/\left (1-\alpha \right ) =\left (2-\alpha \right ) /\left (1-\alpha \right )$.

$$ {{\int}_{z}^{1}}x^{1/\left( 1-\alpha \right) }dx=\frac{1-\alpha }{2-\alpha } \left. x^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right\vert_{z}^{1}=\frac{1-\alpha }{2-\alpha }\left( 1-z^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right) $$

$$ \frac{\bar{\pi}}{w}=\frac{1}{1-z}{{\int}_{z}^{1}}\frac{\pi \left( x,w\right) }{w} dx=\frac{\left( \frac{2}{\alpha }\right)^{1/\left( 2-\alpha \right) }}{1-z} \frac{1-\alpha }{2-\alpha }\left( 1-z^{\left( 2-\alpha \right) /\left( 1-\alpha \right) }\right) $$

Substituting $z=\left (\frac {\alpha }{2}\right )^{\left (1-\alpha \right ) /\left (2-\alpha \right ) }$, we get

$$ \begin{array}{@{}rcl@{}} \frac{\bar{\pi}}{w} &=&\frac{\left( \frac{2}{\alpha }\right)^{1/\left( 2-\alpha \right) }}{1-\left( \frac{\alpha }{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }}\frac{1-\alpha }{2-\alpha }\left( 1-\frac{ \alpha }{2}\right) \\ &=&\frac{1}{\left( \frac{\alpha }{2}\right)^{1/\left( 2-\alpha \right) }-\left( \frac{\alpha }{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) +1/\left( 2-\alpha \right) }}\frac{1-\alpha }{2} \\ &=&\frac{1}{\left( \frac{\alpha }{2}\right)^{1/\left( 2-\alpha \right) }- \frac{\alpha }{2}}\frac{1-\alpha }{2} \\ &=&\frac{1}{\frac{\alpha }{2}\left( \left( \frac{\alpha }{2}\right)^{-\left( 1-\alpha \right) /\left( 2-\alpha \right) }-1\right) }\frac{ 1-\alpha }{2}, \end{array} $$

i.e., Eq. 12.

Appendix 2. Derivation of Eq. 13

First, L’Hopital’s rule implies that

$$ \begin{array}{@{}rcl@{}} \lim\limits_{\alpha \longrightarrow 1}\frac{\bar{\pi}}{w} &\!\! = &\lim\limits_{\alpha \longrightarrow 1}\frac{-1}{\frac{d}{d\alpha }\left( 2^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }\alpha^{1/\left( 2-\alpha \right) }\right) -1} \\ &\!\! = &\lim\limits_{\alpha \longrightarrow 1}\frac{-1}{2^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }\alpha^{1/\left( 2-\alpha \right) }\left( \!-\frac{ \ln 2}{\left( 2-\alpha \right)^{2}} + \frac{\ln \alpha }{\left( 2-\alpha \right)^{2}}\! + \!\frac{1}{\alpha \left( 2-\alpha \right) }\right) - 1} \\ &\!\! = &\frac{-1}{1\left[ -\ln 2+\ln 1+1\right] -1}=\frac{1}{\ln 2}=1.4427 \end{array} $$

Second, that $w\rightarrow 1$ as $\alpha \rightarrow 1$ follows if $\lim _{\alpha \rightarrow 1}\left (1-\alpha \right )^{1-\alpha }=1$. Now L’Hopital’s rule again implies that, setting u = 1 − α,

$$ \lim\limits_{u\rightarrow 0}u\ln u=\lim\limits_{u\rightarrow 0}\frac{\ln u}{u^{-1}} =\lim\limits_{u\rightarrow 0}\frac{1}{u}\left( \frac{1}{-u^{-2}}\right) \rightarrow 0 $$

i.e., $\lim _{\alpha \rightarrow 1}\left (1 - \alpha \right )^{1-\alpha } = 1$. Finally, as $\alpha \!\rightarrow 0$, note that:

$$ \begin{array}{@{}rcl@{}} \frac{\bar{\pi}}{w} &=&\frac{1}{\frac{\alpha }{2}\left( \left( \frac{\alpha }{2}\right)^{-\left( 1-\alpha \right) /\left( 2-\alpha \right) }-1\right) } \frac{1-\alpha }{2}=\frac{1}{\left( \left( \frac{\alpha }{2}\right)^{-\left( 1-\alpha \right) /\left( 2-\alpha \right) }-1\right) }\frac{ 1-\alpha }{\alpha } \\ &=&\frac{1-\alpha }{2^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }\alpha^{1/\left( 2-\alpha \right) }-\alpha } \end{array} $$

Therefore,

$$ \lim\limits_{\alpha \longrightarrow 0}\frac{\bar{\pi}}{w}=\frac{1}{2^{1/2}0^{1/2}-0} =\frac{1}{0}=+\infty . $$

This concludes the proof of Eq. 13.

Appendix 3. Derivation of Eq. 17 and ${\Psi } \left (s\right )$

Then using (14) again, we have where

$$ \begin{array}{@{}rcl@{}} A &=&\left( 1-\alpha \right) \left( \frac{\alpha }{w}\right)^{\alpha /\left( 1-\alpha \right) }=\left( 1-\alpha \right) \left( \frac{\alpha }{ \alpha^{\alpha }(1-\alpha )^{1-\alpha }z}\right)^{\alpha /\left( 1-\alpha \right) } \\ &=&\left( 1-\alpha \right) \left( \frac{\alpha }{\alpha^{\alpha }(1-\alpha )^{1-\alpha }\left( \frac{\alpha }{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }}\right)^{\alpha /\left( 1-\alpha \right) } \end{array} $$

which can be re-written as:

$$ A=2^{\alpha /\left( 2-\alpha \right) }\left( 1-\alpha \right)^{1-\alpha }\alpha^{\alpha \left( 1-\alpha \right) /\left( 2-\alpha \right) } $$

(35)

so that $s\in \left [ w,A\right ]$.

The limits

When $\alpha \rightarrow 0$,

$$ \lim\limits_{\alpha \rightarrow 0}A=\lim_{\alpha \rightarrow 0}\alpha^{\alpha \left( 1-\alpha \right) /\left( 2-\alpha \right) }. $$

Let $M\equiv \alpha ^{\alpha \left (1-\alpha \right ) /\left (2-\alpha \right ) }$. Then,

$$ \lim\limits_{\alpha \rightarrow 0}\left[ -\ln M\right] =\lim\limits_{\alpha \rightarrow 0} \left[ -\frac{\alpha \left( 1-\alpha \right) }{\left( 2-\alpha \right) }\ln \alpha \right] =\lim\limits_{\alpha \rightarrow 0}\frac{-\ln \alpha }{\frac{ 2-\alpha }{\alpha \left( 1-\alpha \right) }} $$

L’Hopital’s rule says that

$$ \lim\limits_{\alpha \rightarrow 0}\left[ -\ln M\right] =\lim\limits_{\alpha \rightarrow 0} \frac{-1/\alpha }{\frac{-\alpha \left( 1-\alpha \right) -\left( 1-2\alpha \right) \left( 2-\alpha \right) }{\alpha^{2}\left( 1-\alpha \right)^{2}}} =\lim\limits_{\alpha \rightarrow 0}\frac{-\alpha \left( 1-\alpha \right)^{2}}{ -\alpha \left( 1-\alpha \right) -\left( 1-2\alpha \right) \left( 2-\alpha \right) }=0 $$

Therefore,

$$ \lim\limits_{\alpha \rightarrow 0}M=e^{-0}=1\Rightarrow \lim\limits_{\alpha \rightarrow 0}A=1 $$

At the other extreme,

$$ \lim\limits_{\alpha \rightarrow 1}A=2\lim\limits_{\alpha \rightarrow 1}\left( 1-\alpha \right)^{1-\alpha } $$

Let $\hat {M}\equiv \left (1-\alpha \right )^{1-\alpha }$. Then,

$$ \lim\limits_{\alpha \rightarrow 1}\left[ -\ln \hat{M}\right] =\lim\limits_{\alpha \rightarrow 1}\left[ -\left( 1-\alpha \right) \ln \left( 1-\alpha \right) \right] =\lim\limits_{\alpha \rightarrow 1}\frac{-\ln \left( 1-\alpha \right) }{ \frac{1}{1-\alpha }} $$

L’Hopital’s rule says that

$$ \lim\limits_{\alpha \rightarrow 1}\left[ -\ln \hat{M}\right] =\lim\limits_{\alpha \rightarrow 1}\frac{\frac{1}{1-\alpha }}{-\frac{1}{\left( 1-\alpha \right) }} =-\lim\limits_{\alpha \rightarrow 1}\left( 1-\alpha \right) =0. $$

Therefore,

$$ \lim\limits_{\alpha \rightarrow 0}\hat{M}=e^{-0}=1\Rightarrow \lim\limits_{\alpha \rightarrow 1}A=2. $$

In summary,

$$ \lim\limits_{\alpha \rightarrow 0}\left\{ \begin{array}{c} z=0 \\ w=0 \\ A=1 \\ s=x \end{array} \right. ,\text{ \ \ \ \ \ \ and \ \ \ \ \ \ }\lim\limits_{\alpha \rightarrow 1}\left\{ \begin{array}{c} z=1 \\ w=1 \\ A=2 \\ s=2 \end{array} \right. . $$

Figure 12 shows how α affects A in relation to its effect on z and w.

Fig. 12

Blue line (z). Dashed green line (ω). Red line (A)

Given (14), the CDF of $s\in \left [ w,A\right ]$ is

$$ {\Psi} \left( s\right) =\frac{\left( s/A\right)^{1-\alpha }-z}{1-z} $$

After substituting for A from Eq. 35 and for z from the Prop, we get

$$ {\Psi} \left( s\right) =\frac{\left( \frac{s}{A}\right)^{1-\alpha }-z}{1-z}= \frac{\left( \frac{s}{2^{\alpha /\left( 2-\alpha \right) }\left( 1-\alpha \right)^{1-\alpha }\alpha^{\alpha \left( 1-\alpha \right) /\left( 2-\alpha \right) }}\right)^{1-\alpha }-\left( \frac{\alpha }{2}\right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }}{1-\left( \frac{\alpha }{2} \right)^{\left( 1-\alpha \right) /\left( 2-\alpha \right) }} $$

(36)

Finally, evaluating (36) at α = 1/2, we get Eq. 17.