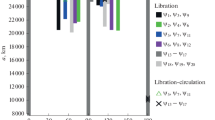
The special features of the structure of secular resonances in the near-earth orbital space bounded by the following range of orbital parameters: semimajor axis from 8000 to 55 000 km, inclination from 0 to 90°, and eccentricity equal to 0.01, 0.6, and 0.8 are analyzed. The influence of stable and unstable secular resonances on the long-term orbital evolution of near-earth space objects is also considered. It is demonstrated that the joint effect of the stable secular resonances of different spectral classes does not violate the regularity of motion. The chaoticity arises when stable secular resonances of one spectral class are imposed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
T. V. Bordovitsyna et al., Astron. Vestn., No. 5, 356–368 (2012).
I. V. Tomilova, I. N. Chuvashov, and T. V. Bordovitsyna, Izv. Vyssh. Uchebn. Zaved., Fiz., 56, No. 10/2, 159–165 (2013).
T. V. Bordovitsyna and I. V. Tomilova, Russ. Phys. J., 57, No. 4, 516–524 (2014).
T. V. Bordovitsyna and I. V. Tomilova, Russ. Phys. J., 57, No. 6, 819–827 (2014).
T. V. Bordovitsyna et al., Astron. Vestn., No. 4, 280–289 (2014).
A. G. Aleksandrova, I. V. Tomilova, and T. V. Bordovitsyna, Izv. Vyssh. Uchebn. Zaved., Fiz., 57, No. 10/2, 95–102 (2014).
G. N. Duboshin, Reference Manual on Celestial Mechanics and Astrodynamics [in Russian], Nauka, Moscow (1976).
N. V. Yemel’yanov, in: Advances in Science and Technology. Ser. Space Research, Vol. 15 [in Russian] (1980), pp. 44–63.
A. Morbidelli, Modern Celestial Mechanics: Aspects of Solar System Dynamics, London: Taylor & Francis (2002).
C. D. Murray and S. F. Dermott, Solar System Dynamics [Russian translation], Fizmatlit, Moscow (2009).
T. V. Bordovitsyna, V. A. Avdyushev, I. N. Chuvashov, et al., Izv. Vyssh. Uchebn. Zaved., Fiz., 52, No. 10/2, 5–11 (2009).
A. J. Rosengren et al., Monthly Notices of the Royal Astronomical Society, 449, No. 4, 3522–3526 (2015).
J. Daqun et al., Celest. Mech. Dyn. Astr. Published Online (02 January 2016).
B. V. Chirikov, Phys. Rep., 52, 263–379 (1979).
P. M. Cincotta et al., Physica, D182, 151–178 (2003).
T. V. Bordovitsyna, A. G. Aleksandrova, and I. N. Chuvashov, Izv. Vyssh. Uchebn. Zaved., Fiz., 53, No. 8/2, 14–21 (2010).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Fizika, No. 3, pp. 41–48, March, 2016.
Rights and permissions
About this article
Cite this article
Bordovitsyna, T.V., Tomilova, I.V. Special Features of the Structure of Secular Resonances in the Dynamics of Near-Earth Space Objects. Russ Phys J 59, 365–373 (2016). https://doi.org/10.1007/s11182-016-0781-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11182-016-0781-0