Skip to main content
SpringerLink
Log in

New class of cosmological solutions for a self-interacting scalar field

  • Elementary Particle Physics and Field Theory
  • Published:
Russian Physics Journal Aims and scope

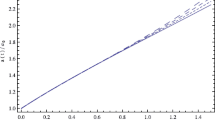
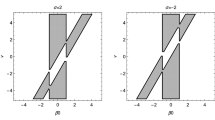
New cosmological solutions are found to the system of Einstein scalar field equations using the scalar field φ as the argument. For a homogeneous and isotropic Universe, the system of equations is reduced to two equations, one of which is an equation of Hamilton–Jacobi type. Using the hyperbolically parameterized representation of this equation together with the consistency condition, explicit dependences of the potential V of the scalar field and the Hubble parameter H on φ are obtained. The dependences of the scalar field and the scale factor a on cosmic time t have also been found. It is shown that this scenario corresponds to the evolution of the Universe with accelerated expansion out to times distant from the initial singularity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. G. Ivanov, in: Gravitation and the Theory of Relativity [in Russian], V. R. Kaigorodov, ed., Kazan’ State University Press, Kazan’ (1981), Vol. 18, pp. 54–60.

  2. J. D. Barrow, Phys. Lett., B187, 12–16 (1987); A. B. Burd and J. D. Barrow, Nucl. Phys., B308, 929–945 (1988); J. D. Barrow, Phys. Rev., D49, 3055 (1994).

  3. A. G. Muslimov, Class. Quantum Grav., 7, 231 (1990).

    Article  MathSciNet  ADS  Google Scholar 

  4. J. J. Halliwell, Phys. Lett., B187, 341–344 (1987).

    Article  MathSciNet  ADS  Google Scholar 

  5. G. Ellis and M. Madsen, Class. Quantum Grav., 8, 667–676 (1991).

    Article  MathSciNet  ADS  MATH  Google Scholar 

  6. S. V. Chervon and V. M. Zhuravlev, Russ. Phys. J., 39, No. 8, 776–789 (1996).

    Article  MathSciNet  Google Scholar 

  7. T. Padmanabhan, аrXiv:hep-th/0204415.

  8. S. V. Chervon and V. M. Zhuravlev, Russ. Phys. J., 43, No. 1, 11–17 (2000); V. M. Zhuravlev and S. V. Chervon, Zh. Eksp. Teor. Fiz., 118, No. 2, 259–272 (2000).

  9. S. V. Chervon, Gen. Relativ. Gravit., 36, 1547–1553 (2004).

    Article  MathSciNet  ADS  MATH  Google Scholar 

  10. S. V. Chervon, O. G. Panina, and M. Sami, Vestnik Samarsk. Gosud. Tekhn. Univ., Ser. Fiz-Mat. Nauki, No. 3, 221–226 (2010).

  11. A. V. Yurov, V. A. Yurov, S. V. Chervon, and M. Sami, Teor. Mat. Fiz., 166, No. 2, 258–268 (2011).

    Article  Google Scholar 

  12. S. V. Chervon, Nonlinear Fields in Gravitation Theory and Cosmology [in Russian], Ul’yanovsk State University Press, Ul’yanovsk (1997).

    Google Scholar 

  13. L. P. Chimento and A. S. Jakubi, arXiv: gr-qc/950615 v1 7 Jun 1995.

  14. L. A. Urena-Lopez and T. Matos, arXiv: astro-ph/0003364 v1 23 Mar 2000.

  15. S. P. Starkovich and F. I. Cooperstock, Astrophys. J., 398, 1–11 (1992).

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ul’yanovsk State Pedagogical University, Ul’yanovsk, Russia

    A. A. Chaadaev & S. V. Chervon

Authors
  1. A. A. Chaadaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. V. Chervon
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. A. Chaadaev.

Additional information

Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Fizika, No. 7, pp. 3–7, July, 2013.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chaadaev, A.A., Chervon, S.V. New class of cosmological solutions for a self-interacting scalar field. Russ Phys J 56, 725–730 (2013). https://doi.org/10.1007/s11182-013-0091-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11182-013-0091-8

Keywords

Search

Navigation