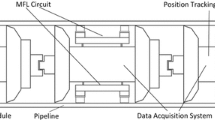
Abstract
The magnetic-flux-leakage (MFL) method has established itself as the most widely used inline inspection technique for the evaluation of gas and oil pipelines. An important problem in MFL nondestructive evaluation is the signal inverse problem, wherein the defect profile and its parameters are determined using the information contained in the measured signals. This paper proposes a genetic-algorithm-based inverse algorithm for reconstructing a 2D defect from MFL signals. In the algorithm, a radial-basis-function neural network is used as a forward model and a genetic algorithm is used to solve the optimization problem in the inverse problem. Experimental results are presented to demonstrate the effectiveness of the proposed inverse algorithm.
Similar content being viewed by others
References
Ramuhalli, P., Udpa, L., and Udpa, S.S., Electromagnetic NDC Signal Inversion by Function-Approximation Neural Networks, IEEE Trans. Magn., 2002, vol. 38, no. 6, pp. 3633–3642.
Lim, J., Data Fusion for NDE Signal Characterization, Dissertation, Iowa State University, 2001.
Hwang, K., Mandayam, S., Udpa, S.S., Udpa, L., Lord, W., and Atzal, M., Characterization of Gas Pipeline Inspection Signals Using Wavelet Basis Function Neural Networks, NDT Int., 2000, vol. 33, no. 8, pp. 531–545.
Ramuhalli, P., Udpa, L., and Udpa, S.S., Neural Network-Based Inversion Algorithms in Magnetic Flux Leakage Nondestructive Evaluation, J. Appl. Phys., 2003, vol. 93, no. 103, pp. 8274–8276.
Goldberg, D.E., Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley, 1989.
Srinivas, M. and Patnaik, L. M., Genetic Algorithms: A Survey, Computer, 1994, vol. 27, no. 6, pp. 17–26.
Haykin, S., Neural Networks: A Comprehensive Foundation, Englewood Cliffs, NJ: Prenticehall, 1994.
Chen, S., Cowan, C.F.N., and Grant, P.M., Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks, IEEE Trans. Neural Networks, 1991, vol. 2, no. 2, pp. 302–309.
Author information
Authors and Affiliations
Additional information
From Defektoskopiya, Vol. 41, No. 12, 2005, pp. 50–57.
Original English Text Copyright © 2005 by Han, Que.
The text was submitted by the authors in English.
Rights and permissions
About this article
Cite this article
Han, W., Que, P. 2D defect reconstruction from MFL signals by a genetic optimization algorithm. Russ J Nondestruct Test 41, 809–814 (2005). https://doi.org/10.1007/s11181-006-0037-0
Received:
Issue Date:
DOI: https://doi.org/10.1007/s11181-006-0037-0