Abstract
The existing research concerning the relationship between risk aversion and prudence and the demand for self-protection assumes that the loss variable follows a Bernoulli distribution, and that changes in the level of self-protection are mean preserving. The analysis here replaces these two very strong conditions with ones which are more general. When doing this, the method of analysis is also significantly modified. This modification includes representing a change in the level of self-protection using the procedure developed by Diamond and Stiglitz (Journal of Economic Theory 8:337-360, 1974) for representing a change in risk. This alternate representation allows the existing findings to be generalized considerably, and also simplifies the analysis.



Similar content being viewed by others
Notes
Louis Eeckhoudt points out that this may be the first use of the D-S approach to represent a change in the level of a decision variable.
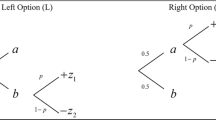
When the level of self-protection can be varied continuously and is chosen optimally, small changes in the level of self-protection do not change the expected utility of the decision maker. Eeckhoudt and Gollier (2005) consider infinitesimal changes in the level of self-protection from the level that is optimal for the risk neutral person. Thus, these changes are mean preserving. Chiu (2005) also imposes the mean preserving condition in his analysis of the demand for self-protection.
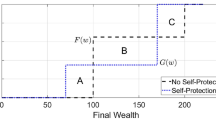
When the loss variable is uniformly distributed with positive probability of zero loss, for instance, an increase in self-protection also leads to a CDF for the outcome variable which crosses the original exactly twice.
These results are related to the Whitmore (1970) definition of third degree stochastic dominance (TSD), but are different in two important respects. First, for Theorem 1 and its corollaries, the means of the two random alternatives are assumed to be equal which is not the case for TSD. Second, the assumption that u′′(W) ≤ 0 is not imposed here. Thus, this theorem imposes stronger conditions on the random variable change, and weaker conditions on risk preferences than does TSD. Thus, these findings, and those of Eeckhoudt and Gollier which they generalize, neither follow from nor do they imply Whitmore’s TSD result.
The marginal utility function completely represents the risk preferences of the decision maker. Meyer (2010) provides additional details and discussion of this issue.
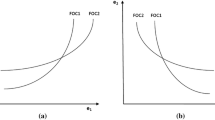
Fishburn and Vickson (1978) show that when the means of two random alternatives F(W) and G(W) are equal, third degree stochastic dominance (TSD) and DARA stochastic dominance are equivalent. The result here is related to theirs, but is different in that risk aversion is not assumed.
References
Briys, E., & Schlesinger, H. (1990). Risk aversion and the propensities for self-insurance and self-protection. Southern Economic Journal, 57, 458–467.
Chiu, W. H. (2000). On the propensity to self-protect. Journal of Risk and Insurance, 67, 555–578.
Chiu, W. H. (2005). Degree of downside risk aversion and self-protection. Insurance: Mathematics and Economics, 36, 93–101.
Diamond, P. A., & Stiglitz, J. E. (1974). Increases in risk and in risk aversion. Journal of Economic Theory, 8, 337–360.
Dionne, G., & Eeckhoudt, L. (1985). Self-insurance, self-protection, and increased risk aversion. Economics Letters, 17, 39–42.
Eeckhoudt, L., & Gollier, C. (2005). The impact of prudence on optimal prevention. Economic Theory, 26, 989–994.
Ehrlich, I., & Becker, G. S. (1972). Market insurance, self-insurance and self-protection. Journal of Political Economy, 80, 623–648.
Fishburn, P., & Vickson, R. G. (1978). Theoretical foundations of stochastic dominance. In G. A. Whitmore & M. C. Findlay (Eds.), Stochastic dominance: An approach to decision making under risk. Toronto: Lexington Books, D.C Heath and Company.
Jullien, B., Salanie, B., & Salanie, F. (1999). Should more risk-averse agents exert more effort? The Geneva Papers on Risk and Insurance Theory, 24, 19–28.
Menezes, C., Geiss, C., & Tressler, J. (1980). Increasing downside risk. American Economic Review, 70, 921–932.
Meyer, J. (2010). Representing risk preferences in expected utility based decision models. Annals of Operations Research, 176, 179–190.
Rothschild, M., & Stigitz, J. E. (1970). Increasing risk I: A definition. Journal of Economic Theory, 2, 225–243.
Whitmore, G. A. (1970). Third degree stochastic dominance. American Economic Review, 60, 457–459.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors thank Louis Eeckhoudt and a referee for comments.
Appendix
Appendix
Theorem
\( \int_{\rm{a}}^{\rm{b}} { - {\hbox{v}}\prime {\hbox{(W)}} \cdot {\hbox{u}}\prime {\hbox{(W)}}{{\hbox{F}}_{\rm{e}}}{\hbox{(W,e)dW}}} > 0\;( < 0) \)for all v′′′(W) > 0 if and only if\( \int_{\rm{a}}^{\rm{b}} { - {\hbox{v}}\prime {\hbox{(W)}} \cdot {\hbox{u}}\prime {\hbox{(W)}}{{\hbox{F}}_{\rm{e}}}{\hbox{(W,e)dW}}} > 0\;( < 0) \) (< 0) for all Av′(W) < 0.
Proof
First the well known direction. v′′′(W) is a necessary condition for Av′(W) < 0. Therefore when \( {\hbox{A}}_{\rm{v}}^{\prime }\left( {\hbox{W}} \right) < 0 \) (< 0) for all v′′′(W) > 0, this implies that \( {\hbox{A}}_{\rm{v}}^{\prime }\left( {\hbox{W}} \right) < 0 \) (< 0) for all persons with Av′(W) < 0 as well. To demonstrate the other direction, assume that \( \int_{\rm{a}}^{\rm{b}} { - {\hbox{v}}\prime {\hbox{(W)}} \cdot {\hbox{u}}\prime {\hbox{(W)}}{{\hbox{F}}_{\rm{e}}}{\hbox{(W,e)dW}}} > 0\;( < 0) \) (< 0) for all Av′(W) < 0. Pick any person with marginal utility v′(W) such that v′′′(W) > 0. Consider all marginal utility functions of the form (v′(W) + k) for k > 0. The value of \( \int_{\rm{a}}^{\rm{b}} { - {\hbox{v}}\prime {\hbox{(W)}} \cdot {\hbox{u}}\prime {\hbox{(W)}}{{\hbox{F}}_{\rm{e}}}{\hbox{(W,e)dW}}} > 0\;( < 0) \) is the same as \( {\hbox{A}}_{\rm{v}}^{\prime }\left( {\hbox{W}} \right) < 0 \) for all k > 0. The slope of the risk aversion measure for these persons is given by: \( \int_{\rm{a}}^{\rm{b}} { - {\hbox{v}}\prime {\hbox{(W)}} \cdot {\hbox{u}}\prime {\hbox{(W)}}{{\hbox{F}}_{\rm{e}}}{\hbox{(W,e)dW}}} > 0\;( < 0) \). Because the second term has k squared in the denominator while the first does not, the second term can be made arbitrarily small in magnitude relative to the magnitude of the first term by choosing k to be large enough. Thus if v′′′(W) > 0, for large enough k, Av′(W) < 0 for this person. A similar argument is easily made for the case where v′′′(W) < 0 and Av′(W) > 0. A sufficiently large value for k is one that exceeds \( \frac{{(v{\prime}{\prime}{{(W)}^2}}}{{v{\prime}{\prime}{\prime}(W)}} - v{\prime}(W) \) for all W.
Rights and permissions
About this article
Cite this article
Meyer, D.J., Meyer, J. A Diamond-Stiglitz approach to the demand for self-protection. J Risk Uncertain 42, 45–60 (2011). https://doi.org/10.1007/s11166-010-9107-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-010-9107-8