Skip to main content
SpringerLink
Log in

Theoretical interpretation of the role of the ionic liquid phase in the (R)-Ru-BINAP catalyzed hydrogenation of methylacetoacetate

  • Published:
Reaction Kinetics, Mechanisms and Catalysis Aims and scope Submit manuscript

Abstract

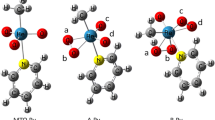
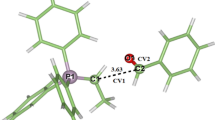
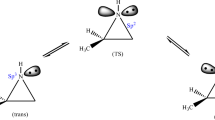
Recently, the work focusing on the role of alkyl chain length in the N[R,222][Tf2N] ionic liquids and its reflection in the kinetic parameters of stereoselective hydrogenation of methylacetoacetate over (R)-[RuCl(binap)(p-cymene)]Cl complex was reported. Irregular trends in the principle parameter of enantioselectivity were observed. Here, a possible theoretical explanation of such irregular trends elucidated with the help of molecular simulations methods is presented. A stepwise approach is proposed for evaluating the energetically most stable conformers of a series of individual N[R,222][Tf2N] for the interpretation of selectivity-structure effects observed experimentally. Initially, Monte Carlo molecular mechanics was used followed by a semi-empirical PM3 method to elucidate also the characteristic thermodynamic functions of state and theoretical molecular spectra. The density functional theory was finally applied. The specific absolute entropy data revealed that due to the partition of the cation and anion twisted closer approach the ionic liquids N[8,222][Tf2N] and N[12,222][Tf2N] may stabilize the structures of the (R)-[RuCl(binap)(p-cymene)]Cl complex.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Noyori R (2003) Adv Synth Catal 345:15

    Article  CAS  Google Scholar 

  2. McDonald AR, Muller C, Voght D (2008) Green Chem 10:424

    Article  CAS  Google Scholar 

  3. Blaser HU, Jallet HP, Spindler F (1996) J Mol Catal A 107:85

    Article  CAS  Google Scholar 

  4. Bartek L, Kluson P, Cerveny L (2005) Chem Listy 99:157

    CAS  Google Scholar 

  5. Jahjah M, Alame M, Pellet-Rostaing P, Lemaire M (2007) Tetrahedron Asymm 19:2305

    Article  Google Scholar 

  6. Wolfson A, Vankelecom IFJ, Geresh S, Jacobs PA (2004) J Mol Catal A 217:21

    Article  CAS  Google Scholar 

  7. Zsigmond A, Notheisz F, Kluson P, Floris T (2010) In: Barbaro P, Liguori F (eds) Heterogenized homogeneous catalysts for fine chemicals production—catalysis by metal complexes, vol 34. Springer, Berlin

    Google Scholar 

  8. Floris T, Kluson P, Muldoon MJ, Pelantova H (2010) Catal Let 134:279

    Article  CAS  Google Scholar 

  9. Floris T, Kluson P, Pelantova H, Bartek L (2009) Appl Catal A 366:160

    Article  CAS  Google Scholar 

  10. Cerna I, Kluson P, Bendova M, Pekarek T, Floris T, Pelantova H (2011) Chem Eng Proc 50:264

    Article  CAS  Google Scholar 

  11. Floris T, Kluson P, Slater M (2011) React Kinet Catal Mech 102:67

    Article  CAS  Google Scholar 

  12. Hallett JP, Welton T (2011) Chem Rev 111:3508

    Article  CAS  Google Scholar 

  13. Olivier-Bourbigou H, Magna L, Morvan D (2010) Appl Catal A 373:1

    Article  CAS  Google Scholar 

  14. Picquet M, Poinsot D, Stutzmann S, Tkatchenko I, Tommasi I, Wasserscheid P, Zimmermann J (2004) Topics Catal 29:139

    Article  CAS  Google Scholar 

  15. Wasserscheid P, Keim W (2000) Angewandte Chem Int Ed 39:3772

    Article  CAS  Google Scholar 

  16. Frisch AC, Webb PB, Zhao G, Muldoon MJ, Pogorzelec PJ, Cole-Hamilton DJ (2007) Dalton Trans 47:5531

    Article  Google Scholar 

  17. Jutz F, Andanson JM, Baiker A (2009) J Catal 268:356

    Article  CAS  Google Scholar 

  18. Allouche AR (2011) J Comp Chem 32(174):182

    Google Scholar 

  19. Halgren TA (1996) J Comp Chem 490:519

    Google Scholar 

  20. Hehre WJ (2003) A guide to molecular mechanics and quantum chemical calculations. Wavefunction Inc, Irvine

    Google Scholar 

  21. Young D (2001) Computational chemistry. Wiley–Interscience, New York, p 330

    Book  Google Scholar 

  22. Frisch MJ et al (2003) Gaussian 03. Gaussian Inc, Wallingford

    Google Scholar 

  23. Young D (2001) Computational chemistry. Wiley–Interscience, New York, p 336

    Book  Google Scholar 

  24. Parr RG, Yang W (1989) Density-functional theory of atoms and molecules. Oxford University Press, Oxford

    Google Scholar 

  25. Johansson KM, Izgorodina EI, Forsyth M, MacFarlane DR, Seddon KR (2008) Phys Chem Chem Phys 10:2972

    Article  CAS  Google Scholar 

  26. Hanke CG, Price SL, Lynden-Bell RM (2001) Mol Phys 99:801

    Article  CAS  Google Scholar 

  27. Bhargava BL, Balasubramanian S (2008) J Phys Chem B 112:7566

    Article  CAS  Google Scholar 

  28. Wang Y, Voth GA (2005) J Am Chem Soc 127:12192

    Article  CAS  Google Scholar 

  29. Bhargava BL, Klein ML (2009) Soft Matter 5:3475

    Article  CAS  Google Scholar 

  30. Berg RW (2007) Monatshefte Chem 138:1045

    Article  CAS  Google Scholar 

  31. Costa Gomes MF, Canongia Lopes JN, Padua AAH (2009) In: Kirchner B (ed) Ionic liquids—topics in current chemistry, vol 290. Springer, Berlin

    Google Scholar 

  32. Kirchner B (2009) In: Kirchner B (ed) Ionic liquids—topics in current chemistry, vol 290. Springer, Berlin

    Google Scholar 

Download references

Acknowledgments

Authors gratefully acknowledge the financial contribution of the Ministry of Industry and Trade of the Czech Republic, Project Grant No. FR-TI3/057. Academy of Sciences of the Czech Republic is also cordially acknowledged for supporting the bilateral CZ-UK cooperation project with Bangor University, UK.

Author information

Authors and Affiliations

  1. Institute of Chemical Process Fundamentals ASCR, Rozvojova 2, 165 02, Prague 6, Czech Republic

    Pavel Dytrych, Petr Kluson & Olga Solcova

  2. School of Chemistry, Bangor University, Bangor, Gwynedd, LL57 2DG, UK

    Morwena Slater

Authors
  1. Pavel Dytrych
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Petr Kluson
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Morwena Slater
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Olga Solcova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Petr Kluson.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dytrych, P., Kluson, P., Slater, M. et al. Theoretical interpretation of the role of the ionic liquid phase in the (R)-Ru-BINAP catalyzed hydrogenation of methylacetoacetate. Reac Kinet Mech Cat 111, 475–487 (2014). https://doi.org/10.1007/s11144-013-0659-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11144-013-0659-x

Keywords

Search

Navigation