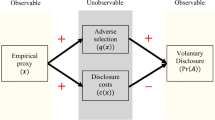
Abstract
We develop a theory of asymmetries between voluntary and mandatory disclosure. Efficiently designed mandatory disclosure policies are substitutes for excessive voluntary disclosures. The efficient policy takes the form of a lower threshold below which firms must disclose bad news and an upper threshold above which firms voluntarily disclose good news. Hence mandatory disclosures are asymmetric and feature conservative reporting of bad news. The threshold to recognize bad news increases when information is more precise. We also characterize interactions between disclosures and real decisions in environments where information has social value: investment decisions, optimal liquidations, and adverse selection in a lemons market.



Similar content being viewed by others
Notes
While the terminology of conservatism is proper to accounting research, the debates are broader than only financial reporting. Regulations that stipulate which types of news must be disclosed are ubiquitous, especially with respect to potentially negative news. Pharmaceutical companies must test drugs and disclose the results of clinical trials, including the drugs’ side-effects (Ma et al. 2015). The Affordable Care Act mandates quality reporting by hospitals (Dranove and Jin 2010). And federal education initiatives and many states’ laws require schools to disclose performance statistics.
Of course, there are also pieces of information that cannot be made credible, and these are not the focus of this study; see Bertomeu (2015) for a discussion of voluntary reporting of “soft” news.
This feature is immediate without productive decisions, given that disclosures are costly, but the intuition holds more generally in the context of productive decisions where more information is desirable. In Section 4, we show that the same result is magnified with productive effects of disclosure.
In the benchmark model, there is no cost to verify that a firm is not subject to mandatory disclosure, as this verification occurs ex post, when private information is public. Below, in Section 5.1, we consider the possibility that verifying that a firm is not subject to mandatory disclosure is costly. Also, while our benchmark analysis considers constant disclosure cost c, the main results hold if the cost is a nondecreasing function c(x), as long as \(\left [x-c(x)\right ]\) is increasing. The proof of this is available upon request.
If the entire cost were redistributive, that is, fully recovered by another party, then optimal policies would prescribe full disclosure. We employ a model of costly disclosure, instead of the alternative approach involving uncertainty about information endowment, because it is nontrivial to consider forcing firms to disclose in a model where managers cannot credibly prove that they are informed; see Ebert et al. (2014) for a recent example. Dye (2017) analyzes a formal model of verification by a fact checker; we conjecture that many insights in the current model would carry over to a related setting in which the firm has access to a costly fact-checking technology.
In Section 4, we extend our analysis to a more general setting, in which P(r) is a convex function of posterior expectations, which implies that information has social value.
The equilibrium that achieves the lowest disclosure cost is well defined as long as an equilibrium exists. The reason is that the function \(t-c-\mathbb {E}(\tilde {x}|\tilde {x}\notin D_{m}, \tilde x\leq t)\) is continuous in t, so that for any convergent sequence {ti} that satisfies \(t_{i}-c-\mathbb {E}(\tilde {x}|\tilde {x}\notin D_{m}, \tilde x\leq t_{i})=0\) for all i, its limit \(t_{\infty }\) satisfies \(t_{\infty }-c-\mathbb {E}(\tilde {x}|\tilde {x}\notin D_{m}, \tilde x\leq t_{\infty })=0\), and therefore \(t_{\infty }=\max \limits _{\mathcal {E}} \tau (D_{m}|\mathcal {E})\).
Log-concavity plays a similar role in adverse selection models, where it is imposed to ensure that local incentive compatibility constraints imply global incentive compatibility (Baron 1982).
This formulation focuses on an investment decision by a manager with no conflict of interest with shareholders, apart from horizon issues. Managing the information environment presents many interesting issues when information may also be used as an incentive device (Arya et al. 1997), and it remains an ongoing question as to when insights from persuasion theory extend to stewardship problems.
To illustrate, in our setting, suppose that a receiver makes an investment I to maximize \(\mathbb {E}(\tilde x I-I^{2}/2|r(\tilde x))\), choosing \(I=\mathbb {E}(\tilde x|r(\tilde x))\), which implies total value \(\mathbb {E}(\tilde x|r(\tilde x))^{2}/2\), that is, mapping to a function ϕ(x) = x2/2. See Kamenica and Gentzkow (2011) and Kartik et al. (2017), supplementary appendix B.3.
The constraint qualification ensures that the problem can be solved with Lagrangian multipliers. We could not find any examples in which the qualification did not hold.
We thus assume that liquidation is no longer available once the voluntary disclosure is made – this is entirely innocuous to the extent that the firm can anticipate the price that follows the disclosure.
This also implies that our main lemons market results can be easily adapted to generalize the optimal liquidation problem in Section 4.2 to the case in which the liquidation payoff depends linearly on the firm’s type.
This assumption is with little loss of generality for our main results. If there are multiple solutions, it can be shown that the largest root is the preferred equilibrium, which implies the maximal amount of trade.
Although the externality argument is a clear reason for intervention (Dye 1990), it is not entirely uncontroversial. Information externalities are not as obvious as pollution or health externalities, and their economic significance is still the subject of ongoing research. Theoretically, information intermediaries may act to collect and trade information, and, in a world where such externalities are significant, the market will find solutions to disseminate information (i.e., firms will sell their information or pool their information into industry associations).
See the proof of Proposition 1.
References
Aghamolla, C, & An, B. (2020). Voluntary disclosure with evolving news. Journal of Financial Economics, forthcoming.
Akerlof, G.A. (1970). The market for lemons: Quality uncertainty and the market mechanism. Quarterly Journal of Economics, 84(3), 488–500.
Armstrong, C.S., Taylor, D.J., & Verrecchia, R.E. (2015). Asymmetric reporting. Journal of Financial Reporting, 1(1), 15–32.
Arya, A., Glover, J.C., & Sivaramakrishnan, K. (1997). The interaction between decision and control problems and the value of information. The Accounting Review, 72(4), 561–574.
Bagnoli, M. (2005). Log-concave probability and its applications. Economic Theory, 26(2), 445–469.
Baron, D. (1982). Regulating a monopolist with unknown costs. Econometrica, 50(4), 911–930.
Bertomeu, J. (2015). Asset measurement in imperfect credit markets. Journal of Accounting Research, 53(5), 965–984.
Bertomeu, J. (2018). Verifiable disclosure. Economic Theory, 65 (4), 1011–1044.
Bertomeu, J., & Magee, R.P. (2015). Mandatory disclosure and asymmetry in financial reporting. Journal of Accounting and Economics, 59(2), 284–299.
Bertomeu, J. (2015). A theory of hard and soft information. The Accounting Review, 91(1), 1–20.
Beyer, A., Cohen, D.A., Lys, T.Z., & walther, B.R. (2010). The financial reporting environment: Review of the recent literature. Journal of Accounting and Economics, 50(2), 296–343.
Bushee, B.J., & Leuz, C. (2005). Economic consequences of SEC disclosure regulation: Evidence from the OTC bulletin board. Journal of Accounting and Economics, 39(2), 233–264.
Cheynel, E. (2013). A theory of voluntary disclosure and cost of capital. Review of Accounting Studies, 18(4), 987–1020.
Christensen, H.B., Hail, L., & Leuz, C. (2013). Mandatory IFRS reporting and changes in enforcement. Journal of Accounting and Economics, 56 (2-3), 147–177.
Clinch, G., & Verrecchia, R.E. (1997). Competitive disadvantage and discretionary disclosure in industries. Australian Journal of Management, 22(2), 125–137.
Dranove, D., & Jin, G.Z. (2010). Quality disclosure and certification: Theory and practice. Journal of Economic Literature, 48(4), 935–963.
Dye, R.A. (1985). Strategic accounting choice and the effects of alternative financial reporting requirements. Journal of Accounting Research, 23 (2), 544–574.
Dye, R.A. (1990). Mandatory versus voluntary disclosures: The cases of financial and real externalities. The Accounting Review, 65(1), 1–24.
Dye, R.A. (2017). Optimal disclosure decisions when there are penalties for nondisclosure. The RAND Journal of Economics, 48(3), 704–732.
Ebert, M., Simons, D., & Stecher, J.D. (2014). Discretionary aggregation. The Accounting Review, 92(1), 73–91.
Einhorn, E. (2005). The nature of the interaction between mandatory and voluntary disclosures. Journal of Accounting Research, 43(4), 593–621.
Friedman, H.L., Hughes, J.S., & Michaeli, B. (2018). A rationale for imperfect reporting standards. Available at SSRN: https://ssrn.com/abstract=3183482.
Friedman, H.L., Hughes, J.S., & Saouma, R. (2016). Implications of biased reporting: Conservative and liberal accounting policies in oligopolies. Review of Accounting Studies, 21(1), 251–279.
Gao, P. (2013). A measurement approach to conservatism and earnings management. Journal of Accounting and Economics, 55(2-3), 251–268.
Gao, P. (2015). Optimal thresholds in accounting recognition standards. Available at SSRN: https://ssrn.com/abstract=2702496.
Gigler, F., Kanodia, C.S., Sapra, H., & Venugopalan, R. (2009). Accounting conservatism and the efficiency of debt contracts. Journal of Accounting Research, 47(3), 767–797.
Glode, V., Opp, C.C., & Zhang, X. (2018). Voluntary disclosure in bilateral transactions. Journal of Economic Theory, 175, 652–688.
Guay, W.R., & Verrecchia, R.E. (2018). Conservative disclosure. Journal of Financial Reporting, 3(1), 73–92.
Heinle, M.S., Samuels, D., & Taylor, D. (2020). Proprietary costs and disclosure substitution: Theory and empirical evidence. Available at SSRN: https://ssrn.com/abstract=3173664.
Heinle, M.S., & Verrecchia, R.E. (2015). Bias and the commitment to disclosure. Management Science, 62(10), 2859–2870.
Huddart, S., Hughes, J.S., & Brunnermeier, M. (1999). Disclosure requirements and stock exchange listing choice in an international context. Journal of Accounting and Economics, 26(1), 237–269.
Jiang, X., & Yang, M. (2016). Properties of optimal accounting rules in a signaling game. Journal of Accounting and Economics, 63(2-3), 499–512.
Jorgensen, B.N., & Kirschenheiter, M.T. (2015). Discretionary disclosures to risk-averse traders: A research note. Contemporary Accounting Research, 32(3), 1224–1235.
Jovanovic, B. (1982). Truthful disclosure of information. Bell Journal of Economics, 13(1), 36–44.
Jung, W., & Kwon, Y.K. (1988). Disclosure when the market is unsure of information endowment of managers. Journal of Accounting Research, 26(1), 146–153.
Kamenica, E., & Gentzkow, M. (2011). Bayesian persuasion. The American Economic Review, 101(6), 2590–2615.
Kartik, N., Lee, F.X., & Suen, W. (2017). Investment in concealable information by biased experts. The RAND Journal of Economics, 48(1), 24–43.
Lerman, A., & Livnat, J. (2010). The new form 8-k disclosures. Review of Accounting Studies, 15(4), 752–778.
Leuz, C., & Verrecchia, R. (2000). The economic consequences of increased disclosure. Journal of Accounting Research, 38, 91–124.
Levin, J. (2001). Information and the market for lemons. The RAND Journal of Economics, 32(4), 657–666.
Li, E.X., Ramesh, K., & Shen, M. (2011). The role of newswires in screening and disseminating value-relevant information in periodic SEC reports. The Accounting Review, 86(2), 669–701.
Li, W. (2014). A theory on the discontinuity in earnings distributions. Contemporary Accounting Research, 31(2), 469–497.
Lizzeri, A. (1999). Information revelation and certification intermediaries. The RAND Journal of Economics, 30(2), 214–231.
Ma, P., Marinovic, I., & Karaca-Mandic, P. (2015). Drug manufacturers’ delayed disclosure of serious and unexpected adverse events to the US food and drug administration. JAMA Internal Medicine, 175(9), 1565–1566.
Marinovic, I., & Varas, F. (2016). No news is good news: Voluntary disclosure in the face of litigation. The RAND Journal of Economics, 47(4), 822–856.
Milgrom, P.R. (1981). Good news and bad news: Representation theorems and applications. Bell Journal of Economics, 12(2), 380–391.
Moonitz, M. (1951). The valuation of business capital: An accounting analysis. American Economic Review, 41(2), 157–165.
Noh, S., So, E.C., & Weber, J.P. (2019). Voluntary And mandatory disclosures: Do managers view them as substitutes. Journal of Accounting and Economics, 68(1), 101243.
Rappoport, D. (2017). Evidence and skepticism in verifiable disclosure games. Ph.D dissertation, Columbia University.
Shavell, S. (1994). Acquisition and disclosure of information prior to sale. The RAND Journal of Economics, 25, 20–36.
Skinner, D.J. (1994). Why firms voluntarily disclose bad news. Journal of Accounting Research, 32(1), 38–60.
Suijs, J. (2005). Voluntary disclosure of bad news. Journal of Business Finance & Accounting, 32(7-8), 1423–1435.
Suijs, J., & Wielhouwer, J.L. (2019). Disclosure policy choices under regulatory threat. The RAND Journal of Economics, 50(1), 3–28.
Verrecchia, R.E. (1983). Discretionary disclosure. Journal of Accounting and Economics, 5, 179–194.
Verrecchia, R.E. (1990). Information quality and discretionary disclosure. Journal of Accounting and Economics, 12(4), 365–380.
Wagenhofer, A. (1990). Voluntary disclosure with a strategic opponent. Journal of Accounting and Economics, 12(4), 341–363.
Watts, R.L. (2003). Conservatism in accounting part ii: Evidence and research opportunities. Accounting Horizons, 17(4), 287–301.
Acknowledgments
We thank seminar participants and colleagues at Carnegie Mellon University, Baruch College, University of Sydney and the ARW conference at the University of Basel for useful comments. We also thank Edwige Cheynel, Ron Dye, Michael Ebert (discussant), Pingyang Gao, Ilan Guttman, Steven Huddart (discussant), Navin Kartik, Pierre Liang, Iván Marinovic, Stefan Reichelstein (editor), and two anonymous referees for helpful comments. Wenjie Xue acknowledges the grant S.No.02.2019.133 from NUS.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 1
Let \(D_{m}^{*}\) be an efficient policy with \(\tau \equiv \tau (D_{m}^{*})\) and λ ≡{x : x > τ}. Suppose that there exists \((a_{1},a_{2})\subset D_{m}^{*}\) and 𝜖 > 0, where \(-\infty <a_{1}<a_{2}\leq \tau \) and \([a_{1}-\epsilon , a_{1}]\cap D_{m}^{*}=\emptyset \). Below, we construct an alternative disclosure set with a lower probability of disclosure.
Define 𝜖1,𝜖2 > 0 such that (i) 𝜖1 < 𝜖, (ii) a1 + 𝜖2 < a2, and (iii) F(a1 + 𝜖2) − F(a1) = F(a1) − F(a1 − 𝜖1) and an alternative mandatory disclosure set \(D_{m}^{\prime }\) by \(D_{m}^{\prime }=D_{m}^{*}\cup (a_{1}-\epsilon _{1},a_{1}) \setminus [a_{1},a_{1}+\epsilon _{2}]\). By construction, \(\tau -c-\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ,\tilde {x}\notin D_{m}^{\prime })<\tau -c-\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ,\tilde {x}\notin D_{m}^{*})=0\). Moreover, \(t-c-\mathbb {E}(\tilde {x}|\tilde {x}\leq t,\tilde {x}\notin D_{m}^{\prime })\) is positive for \(t>\mathbb {E}(\tilde {x}|\tilde {x}\notin D_{m}^{\prime })+c\). Hence \(\tau ^{\prime }\equiv \tau (D_{m}^{\prime })\) exists by intermediate value theorem, and it is true that \(\tau ^{\prime }>\tau \). Denote \(\lambda ^{\prime }\equiv \{x:x>\tau ^{\prime }\}\). It then follows that
Therefore the set \(D_{m}^{\prime }\) would feature lower expected disclosure costs than \(D_{m}^{*}\), a contradiction. □
Proof of Proposition 1
Since \(t-\mathbb E(\tilde x|\theta \leq \tilde x\leq t)\) is positive for sufficiently large t, it must be that
For a particular \(\theta \in \mathbb R\), there are two cases we need to consider.
Case 1
\(\frac {\partial (t-\mathbb E(\tilde x|\theta \leq \tilde x\leq t))}{\partial t}|_{t=\tau _{\theta }}> 0\).
which can be rewritten as F(τ𝜃) − F(𝜃) − cf(τ𝜃) > 0.
Applying the implicit function theorem on Γ1(τ𝜃,𝜃) = 0, it then follows that
because τ𝜃 − c = P𝜃(nd) > 𝜃.
Let \(\mathcal C(\theta )\) denote the expected disclosure cost as a function of 𝜃:
Because the denominator in the right-hand side of Eq. 7.2 is positive, the sign of \(\mathcal C^{\prime }(\theta )\) is equal to the sign of F(τ𝜃) − F(𝜃) − (τ𝜃 − 𝜃)f(τ𝜃). If τ𝜃 is bounded below by \(\underline \tau >-\infty \), it is obvious that F(τ𝜃) − F(𝜃) − (τ𝜃 − 𝜃)f(τ𝜃) is negative for 𝜃 sufficiently small. If τ𝜃 is not bounded from below, it is true that τ𝜃 < m when 𝜃 is sufficiently small, which suggests that \(F(\tau _{\theta })-F(\theta )\equiv {\int \limits }_{\theta }^{\tau _{\theta }}f(x)\mathrm d x<{\int \limits }_{\theta }^{\tau _{\theta }}f(\tau _{\theta })\mathrm d x\equiv (\tau _{\theta }-\theta )f(\tau _{\theta })\) for 𝜃 is sufficiently small.
Case 2
\(\frac {\partial (t-\mathbb E(\tilde x|\theta \leq \tilde x\leq t))}{\partial t}|_{t=\tau _{\theta }}=0\).
In this case, \(\frac {\partial {\Gamma }_{1}(t,\theta )}{\partial t}|_{t=\tau _{\theta }}= 0\), and the implicit function theorem fails. But we can consider the right-derivative:
which implies that
Hence it must be true that \(\lim _{\varepsilon \to 0^{+}}\frac {\tau _{\theta +\varepsilon }-\tau _{\theta }}{\varepsilon }=\infty \), and
As a result, \(\theta ^{*}=-\infty \) is not optimal.
With the c.d.f. strictly log-concave, \(\frac {\partial (t-\mathbb E(\tilde x|\theta \leq x\leq t))}{\partial t}> 0\) for any \(\theta \in \mathbb R,\) and τ𝜃 is the unique solution to Eq. 3.2 (Bagnoli 2005). By Eq. 7.2, the mandatory disclosure threshold 𝜃∗ must satisfy the following first-order condition:
From the mean value theorem, there exists \(z^{*}\in (\theta ^{*},\tau _{\theta ^{*}})\) such that
Since the p.d.f. is single-peaked, z∗ and \(\tau _{\theta ^{*}}\) must be on the opposite sides of the mode m, i.e., \(z^{*}<m<\tau _{\theta ^{*}}\), which implies: \(\theta ^{*}<m<\tau _{\theta ^{*}}\) and
We prove next that the solution to Eq. 7.3 is unique. For any 𝜃 < m, define τ2(𝜃) as a solution to Γ2(t,𝜃) = 0 with 𝜃 < m < t and f(𝜃) < f(t), where
Note that (i) F(m) − F(𝜃) − (m − 𝜃)f(m) < 0, because \(F(m)-F(\theta )= {\int \limits }_{\theta }^{m}f(x)\mathrm d x<{\int \limits }_{\theta }^{m} f(m)\mathrm dx= (m-\theta )f(m)\), (ii) \(\lim _{t\to \infty }{\Gamma }_{2}(t,\theta )=\lim _{t\to \infty }F(t)-F(\theta )-\lim _{t\to \infty }tf(t)+\lim _{t\to \infty }\theta f(t)=1-F(\theta )>0\), because \(\lim _{t\to \infty }tf(t)= 0\), and (iii) \(\partial {\Gamma }_{2}/\partial t=-(t-\theta )f^{\prime }(t)\) is strictly positive for t > m. Hence τ2(𝜃) is unique and is a function from \((-\infty ,m)\) to \((m,\infty )\). Further, the voluntary threshold \(\tau _{\theta ^{*}}\) must satisfy the cost-minimizing optimality condition τ2(𝜃∗), which implies that \(\tau _{2}(\theta ^{*})=\tau _{\theta ^{*}}\). We know from Eq. 7.1 that τ𝜃 is increasing in 𝜃 and, applying the implicit function theorem on Γ2(τ2(𝜃),𝜃) = 0,
This implies that τ𝜃 and τ2(𝜃) cross once and hence the solution to \(\tau _{\theta ^{*}}=\tau _{2}(\theta ^{*})\) is unique. □
Proof of Corollary 1
The fact that \(\theta ^{*}<m<\tau _{\theta ^{*}}\) is established in the proof of Proposition 1. For the special case in which the distribution of \(\tilde {x}\) is symmetric, \(\tau _{\theta ^{*}}-m=m-z^{*}\), where z∗ is given by Eq. 7.4. Thus \(Prob(\tilde {x}< z^{*})=Prob(\tilde {x}> \tau _{\theta ^{*}})\), implying that the probability of mandatory disclosure \(Prob(\tilde {x}< \theta ^{*})<Prob(\tilde {x}< z^{*})\) is lower than the probability of voluntary disclosure. □
Proof of Corollary 2
Applying the implicit function theorem on \({\Gamma }_{1}(\tau _{\theta ^{*}},\theta ^{*})=0\) and \({\Gamma }_{2}(\tau _{\theta ^{*}},\theta ^{*})=0\):
where \({\Delta }=F(\tau _{\theta }^{*})-F(\theta ^{*})\) and
We know that (i) \(f^{\prime }(\tau _{\theta ^{*}})<0\) from Corollary 1 and (ii) \(f(\tau _{\theta ^{*}})-f(\theta ^{*})>0\) from Eq. 7.5 so that \(Sign(\frac {\partial \tau _{\theta ^{*}}}{\partial c})=-Sign(\frac {\partial \theta ^{*}}{\partial c})=Sign(Z)\), and Z > 0 is implied by (iii) \(\tau _{\theta ^{*}}-c>\theta ^{*}\) from Eq. 3.1, and (iv) \(F(\tau _{\theta ^{*}})-F(\theta ^{*})-cf(\tau _{\theta ^{*}})>0\) from (iii) and Eq. 3.3. □
Proof of Corollary 3
Without loss of generality, we set μ = 0. Denote the p.d.f. and c.d.f. of the standard normal distribution as ϕ(⋅) and Φ(⋅) respectively. The probability of mandatory and voluntary disclosure can be written respectively as:
We use the following change of variable on \({\Gamma }_{1}(\tau _{\theta ^{*}},\theta ^{*})=0\) and \({\Gamma }_{2}(\tau _{\theta ^{*}},\theta ^{*})=0\):
From the proof of Corollary 2, we have that \(\frac {\theta ^{*}}{\sigma }\) decreases in \(\frac {c}{\sigma }\) and \(\frac {\tau _{\theta ^{*}}}{\sigma }\) increases in \(\frac {c}{\sigma }\). Hence it proves that \(\frac {\theta ^{*}}{\sigma }\) increases in σ and \(\frac {\tau _{\theta ^{*}}}{\sigma }\) decreases in σ. □
Proof of Proposition 2
We prove this result in several steps.
- Step 1::
-
We argue that \(\tau ^{*}={\max \limits } \{\tau : \phi (\tau )-c-\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ,{\Theta }^{*}(\tilde {x})=1))=0\}\), i.e., τ∗ is the maximal threshold that can be sustained in equilibrium. To see this, note that, for any two solutions \(\tau ^{\prime \prime }>\tau ^{\prime }\) to \(\phi (\tau )-c-\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ,{\Theta }^{*}(\tilde {x})=1))=0\), it holds that (i) \(\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{\prime \prime },{\Theta }^{*}(\tilde {x})=1))>\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{\prime },{\Theta }^{*}(\tilde {x})=1))\), and (ii) \(\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{\prime \prime },{\Theta }^{*}(\tilde {x})=1))\geq \phi (x)-c\) for any \(x\in (\tau ^{\prime },\tau ^{\prime \prime }]\). This implies that the objective function is greater under \(\tau ^{\prime \prime }\) than under \(\tau ^{\prime }\).
- Step 2::
-
In this step, we show that it is not optimal to disclose an interval adjacent to the left of τ∗. By contradiction, suppose that Θ∗(x) = 0 for x ∈ (τ∗− ε,τ∗) for some ε > 0. Set Θ∗∗(x) ≡Θ∗(x) except that Θ∗∗(x) = 1 for x ∈ (τ∗− ε,τ∗∗), where τ∗∗ solves \(\phi (\tau ^{**})-c-\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{**},{\Theta }^{**}(\tilde {x})=1))=0\). Θ∗∗(x) is more efficient than Θ∗(x) because:
-
(i) \(\phi (\tau ^{*})-c-\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{*},{\Theta }^{**}(\tilde {x})=1))<0\) implies τ∗∗ > τ∗;
-
(ii) \(\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{**},{\Theta }^{**}(\tilde {x})=1))>\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{*},{\Theta }^{*}(\tilde {x})=1))\); and
-
(iii) for any x ∈ (τ∗− ε,τ∗∗), \(\phi (\mathbb {E}(\tilde {x}|\tilde {x}\leq \tau ^{**},{\Theta }^{**}(\tilde {x})=1))\geq \phi (x)-c\).
- Step 3::
-
We show a necessary property of τ∗.
From step 1, τ∗ is the maximal solution to the constraint (4.1) at optimality. Also
Thus the following inequality holds:
Expanding the above inequality, we get
The above implies that τ∗ satisfies
- Step 4::
-
Taking the F.O.C.s of the Lagrangian, we get:
$$ \begin{array}{@{}rcl@{}} &&\frac{\partial \mathcal L}{\partial {\Theta}(x)}=f(x)\left( \phi(x^{*}_{nd})-\phi(x)+\gamma_{2} (x^{*}_{nd}-x)+c\right),\text{ for each \textit{x}}\leq \tau^{*};\\ &&\frac{\partial \mathcal L}{\partial \tau}|_{\tau=\tau^{*}}= \gamma_{1}\phi^{\prime}(\tau^{*})+\gamma_{2}f(\tau^{*})\left( x^{*}_{nd}-\tau^{*}\right)=0;\\ &&\frac{\partial \mathcal L}{\partial x_{nd}}|_{x_{nd}=x_{nd}^{*}}=\phi^{\prime}(x^{*}_{nd}){\int}_{-\infty}^{\tau^{*}} {\Theta}^{*}(x) f(x)\mathrm{d}x-\gamma_{1}\phi^{\prime}(x^{*}_{nd})+\gamma_{2} {\int}_{-\infty}^{\tau^{*}} {\Theta}^{*}(x)f(x)\mathrm{d}x=0. \end{array} $$
Define
Solving for γ2, we get
Hence the sign of \(\frac {\partial L}{\partial {\Theta }(x)}\) depends on the sign of
ϕ(⋅) is convex, i.e., \(\phi ^{\prime \prime }(x)\geq 0\), which implies that:
Hence, in this case, Σ(x) is concave and increasing for \(x<x^{*}_{nd}\in \mathbb R\), with \({\Sigma }(x^{*}_{nd})=c>0\), which implies that there exists a \(\theta ^{*}\in \mathbb (-\infty ,x^{*}_{nd})\) such that Σ(x) < 0 for x < 𝜃∗. In step 2, we have shown that it is not optimal to disclose an interval adjacent to the left of \((\tau ^{*},+\infty )\).
It proves that an efficient policy features \(D_{m}^{*}=(-\infty ,\theta ^{*})\), where \(-\infty <\theta ^{*}<\tau ^{*}<\infty \). □
Proof of Lemma 2
By contradiction, suppose that there exists \(\underline l>\overline l\) such that \((\underline l, \overline l)\subseteq (-\infty ,0)\) and \((\underline l, \overline l)\notin D_{m}^{*}\). Denote the set of of types liquidated as L. For any x < c, disclosure by mandate would induce liquidation. Also, nondisclosure price has to be positive if there is nondisclosure in equilibrium.
Case 1
The preferred equilibrium is such that (i) the voluntary disclosure set is \((c,\infty )\), and (ii) \(L=(-\infty ,c)\). In this equilibrium, there is no nondisclosure on equilibrium path. Define \(D_{m}^{\prime }\equiv (-\infty ,0)\cup D_{m}^{*}\). Then, given this \(D^{\prime }_{m}\), those with x < 0 liquidate. In the preferred equilibrium, there is a positive nondisclosure price \(P_{D_{m}^{\prime }}(nd)=\tau (D_{m}^{\prime })-c>0\) such that those with \(x>\tau (D^{\prime }_{m})\) voluntarily disclose, those with \(x\in [0,c]\cap D_{m}^{\prime }\) liquidate, and those with \(x\in [0,\tau (D^{\prime }_{m})]\setminus D_{m}^{\prime }\) sell without disclosure at price \(P_{D_{m}^{\prime }}(nd)=\mathbb E(\tilde {x}|\tilde {x}\notin D^{\prime }_{m},\tilde x\leq \tau (D^{\prime }_{m}))\). This equilibrium features weakly more trade for positive types (i.e., those in \([0,c]\setminus D_{m}^{*}\) now trade) and less disclosure (i.e., \(\tau (D_{m}^{\prime })>c\)). Hence \(D_{m}^{\prime }\) is more efficient than \(D^{*}_{m}\), a contradiction.
Case 2
The preferred equilibrium is such that there is a positive nondisclosure price \(P_{D_{m}^{*}}(nd)=\tau (D_{m}^{*})-c>0\) such that (i) the voluntary disclosure set is \((\tau (D_{m}^{*}),\infty )\), where \(\tau (D_{m}^{*})>c\), (ii) the liquidation set is \(L\equiv (-\infty ,c)\cap D_{m}^{*}\), and (iii) others sell at \(P_{D^{*}_{m}}(nd)\) without disclosure with the price being determined by \(P_{D^{*}_{m}}(nd)=\mathbb E(\tilde {x}|\tilde {x}\notin D^{*}_{m},\tilde x\leq \tau (D^{*}_{m}))>0\). In this case, no sellers would voluntarily liquidate unless mandated to disclose for the reason that a positive nondisclosure price is always a better alternative to liquidation. Define \(D_{m}^{\prime }\equiv (-\infty ,0)\cup D_{m}^{*}\). Given \(D_{m}^{\prime }\), \(x\in (\underline l, \overline l)\) would be liquidated, so are others with \(x\in (-\infty ,0)\). Moreover, the preferred equilibrium, given this \(D_{m}^{\prime }\), must feature a positive nondisclosure price \(P_{D_{m}^{\prime }}(nd)>0\) such that \(P_{D_{m}^{\prime }}(nd)>P_{D_{m}^{*}}(nd)\). Hence the policy \(D_{m}^{\prime }\) features less trade for x < 0 and less disclosure, which makes it more efficient than \(D_{m}^{*}\), a contradiction.
We have proved that \((-\infty ,0)\subseteq D_{m}^{*}\). For x2 > x1 ≥ 0, liquidating x1 implies lower loss in trade efficiency than liquidating x1. Hence the argument in the proof for lemma 1 holds here as well; that is, one can always construct a more efficient policy if the \(D_{m}^{*}\) is not a threshold type.
□
Proof of Proposition 3
For 𝜃 > c, 𝜃 maximizes
where τ𝜃 uniquely solves (3.2) and \(P_{\theta }(nd)=\frac {{\int \limits }_{\theta }^{\tau _{\theta }} xf(x) \mathrm {d}x}{{\int \limits }_{\theta }^{\tau _{\theta }} f(x) \mathrm {d}x}\).
Hence, for 𝜃 > c, the objective function is equivalent to the objective function in the baseline, i.e., Footnote 17
From Eq. 7.2,
For 0 ≤ 𝜃 ≤ c, 𝜃 should maximize
where τ𝜃 uniquely solves (3.2) and \(P_{\theta }(nd)=\frac {{\int \limits }_{\theta }^{\tau _{\theta }} xf(x) \mathrm {d}x}{{\int \limits }_{\theta }^{\tau _{\theta }} f(x) \mathrm {d}x}\).
Taking the first-order derivative of the above objective function, we get
From the proof in Proposition 1, we have shown that F(τ𝜃) − F(𝜃) − cf(τ𝜃) > 0. Hence
An immediate observation is that \(\mathcal P_{1}(c)=\mathcal P_{2}(c)\) and \(\mathcal P_{1}^{\prime }(c)=\mathcal P_{2}^{\prime }(c)\). Further
where
Case 1
χ(c) > 0: We know from the proof of uniqueness in Proposition 1 that
This implies that
In this case, the solution to 𝜃∗ > c is given by Eq. 3.3.
Case 2
χ(c) < 0: We know from the proof of uniqueness in Proposition 1 that
This implies that
In this case, the solution to 𝜃∗ < c is given by Eq. 4.3. We have shown that \(0=\mathcal P_{2}^{\prime }(\theta ^{*})>\mathcal P_{1}^{\prime }(\theta ^{*})\) because 𝜃∗ < c. Hence 𝜃∗ in this case is greater than the baseline mandatory disclosure threshold.
From Corollary 2, we have that χ(c) ≥ (≤)0 when c ≤ (≥)c0 where c0 uniquely solves χ(c0) = 0.
□
Proof of Proposition 4
The proof that the efficient policy is a threshold type of rule follows along the lines of Lemma 1.
Λ(k,𝜃) is positive for sufficiently large k:
Hence we can conclude that δ(F(κ(𝜃)) − F(𝜃)) − f(κ(𝜃))κ(𝜃)(1 − δ) > 0. Applying the implicit function theorem on Λ(κ(𝜃),𝜃) = 0, we get
because \(\delta \kappa (\theta )=\mathbb {E}(\tilde x| \tilde x\in [\theta ,\kappa (\theta )])>\theta \).
First, if κ(𝜃) < c/(1 − δ), those with x < 𝜃 would retain the asset to avoid disclosure because 𝜃 < κ(𝜃) < c/(1 − δ). Those with x ∈ [𝜃,κ(𝜃)] would sell without disclosure, those with x ∈ (κ(𝜃),c/(1 − δ)] would retain the asset, and those with x > c/(1 − δ) would sell with voluntary disclosure.
The objective function in this case is
Taking the first-order condition yields
Evaluating the numerator at 𝜃 = 0 yields
We denote the 𝜃 that solves the first order condition as 𝜃3; that is,
Second, if 𝜃 < c/(1 − δ) but κ(𝜃) > c/(1 − δ), the firm in the middle sell without disclosure. The objective function in this case is
where τ𝜃 is given by Eq. 3.2.
Taking the first-order condition yields
Evaluating the numerator at 𝜃 = 0:
We denote 𝜃 that solves the first-order condition as 𝜃2; that is,
The third case to consider is when 𝜃 > c/(1 − δ). The objective function is
The first-order condition is the same as the baseline model:
Denote the solution to the first-order condition as 𝜃1.
It can be easily shown that \(\mathcal W_{2}(c/(1- \delta ))=\mathcal W_{1}(c/(1- \delta ))\). Further,
where
Case 1
ψ(c/(1 − δ)) > 0. We know from the proof of uniqueness in Proposition 1 that \( \mathcal W_{1}^{\prime }(\theta ) = f(\theta )\frac {c((\tau _{\theta }-\theta )f(\tau _{\theta })-(F(\tau _{\theta })-F(\theta )))}{F(\tau _{\theta })-F(\theta )-c f(\tau _{\theta })}>0 \) for 𝜃 ≤ c/(1 − δ). This implies that
Consider the numerator of \(\mathcal W_{3}^{\prime }(\theta )\) for 𝜃 < κ(𝜃) ≤ c/(1 − δ):
From corollary 1, c/(1 − δ) < 𝜃1 < m, which implies that 𝜃 < κ(𝜃) < m. Hence f(κ(𝜃))(κ(𝜃) − 𝜃) − (F(κ(𝜃)) − F(𝜃)) > 0; that is, \(\mathcal W_{3}^{\prime }(\theta )>0\) for 𝜃 < κ(𝜃) ≤ c/(1 − δ).
This proves that the optimal threshold is the baseline one; that is, 𝜃∗ = 𝜃1.
Case 2
ψ(c/(1 − δ)) < 0. We know from the proof of uniqueness in Proposition 1 that \( \mathcal W_{1}^{\prime }(\theta ) = f(\theta )\frac {c((\tau _{\theta }-\theta )f(\tau _{\theta })-(F(\tau _{\theta })-F(\theta )))}{F(\tau _{\theta })-F(\theta )-c f(\tau _{\theta })}<0 \) for 𝜃 ≥ c/(1 − δ). This implies that
In this case, the optimal threshold is 𝜃∗ < c/(1 − δ).
When m > 0, from the proof of corollary 2, ψ(c/(1 − δ)) > (<)0 when c < (>)c1, where c1 solves ψ(c1/(1 − δ)) = 0. When m = 0, it must be true that ψ(c/(1 − δ)) < 0.
□
Proof of Proposition 5
As in the benchmark, there is a unique equilibrium for any 𝜃, because one can think of this problem as the original problem with disclosure cost equal to [c − h(𝜃)] > 0. It then follows from the implicit function theorem that
The denominator is positive from log-concavity. The sign of the numerator is undetermined. As 𝜃 increases, the net cost of disclosure decreases, which may yield more voluntary disclosure.
Then the first-order condition is
Since \(\lim _{\theta \to -\infty } h(\theta )= 0\) and \(\lim _{\theta \to -\infty } h^{\prime }(\theta )= 0\), the first-order condition converges to that in the benchmark as \(\theta \to -\infty \). Hence \(\theta =-\infty \) is never optimal. □
Proof of Proposition 6
It can be easily checked that Lemma 1 applies. We prove the if and only if parts separately.
If As shown in the proof of Proposition 1, the sign of the F.O.C. for minimizing the expected disclosure cost when evaluated at \(\theta =\underline x\) is determined by the sign of \([F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})]\). The set \(\{(F(\cdot ),c)|F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})<0\}\) is not empty, as shown below.
Assuming \(\underline {x}<m<+\infty \), \(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})<0\) if \(\underline {x}<\tau _{\underline {x}}\leq m\). If \(\tau _{\underline {x}}>m\), \(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})\) is increasing in \(\tau _{\underline {x}}\), i.e., \(\frac {\partial \left (F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})\right ) }{\partial \tau _{\underline {x}}}=-(\tau _{\underline x}-\underline {x})f^{\prime }(\tau _{\underline {x}})>0\). Also \(\lim _{\tau _{\underline {x}\to +\infty }}F(\tau _{\underline {x}})-F(\underline {x})+(\underline {x}-\tau _{\underline {x}})f(\tau _{\underline {x}})=F(+\infty )-F(\underline {x})+(\underline {x}-\infty )f(+\infty )=1-F(\underline {x})>0\). By intermediate value theorem, the exists a unique \(\hat \tau _{\underline {x}}> m\) such that \(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})\geq (\leq )0\) if \(\tau _{\underline x}\geq (\leq ) \hat \tau _{\underline x}\). Since \(\tau _{\underline {x}}\) increases in c, there exists a unique \(\overline c>0\) such that \(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})<0\) if (and only if) \(c<\overline c\).
\(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})<0\) implies that \(\underline x<m<+\infty \). The proof of uniqueness is identical to the uniqueness proof in Proposition 1, with the the support replaced by \([\underline x,+\infty )\).
Only if \(F(\tau _{\underline {x}})-F(\underline {x})-(\tau _{\underline {x}}-\underline {x})f(\tau _{\underline {x}})\geq 0\) contradicts the fact that there exists a unique solution to Eq. 3.3 in \([\underline x,+\infty )\). □
Rights and permissions
About this article
Cite this article
Bertomeu, J., Vaysman, I. & Xue, W. Voluntary versus mandatory disclosure. Rev Account Stud 26, 658–692 (2021). https://doi.org/10.1007/s11142-020-09579-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11142-020-09579-0