Skip to main content
SpringerLink
Log in

The method of multifrequency near-field acoustical tomography of bulk inhomogeneities of the sea bottom

  • Published:
Radiophysics and Quantum Electronics Aims and scope

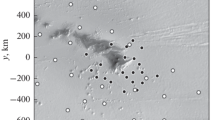
In this work, we propose a method of near-field acoustical multi-frequency coherent tomography of spatially localized inhomogeneities of the shallow-sea bottom. In the framework of the developed method, two-dimensional spatial scanning of the radiating-receiving system along the bottom over the region of location of the inhomogeneities is performed at multiple frequencies. Using the Born approximation, the initial three-dimensional integral equation for the scattered field is reduced to one-dimensional Fredholm equation of the first kind with respect to the depth profile of the transverse spatial spectrum of the inhomogeneities. In the solution of this integral equation for each pair of spectral components, we use the method of generalized residual and obtain the sought three-dimensinal distribution via the inverse Fourier transform of the reconstructed spectrum. Results of numerical simulation of the tomography scheme and visualized inhomogeneities of shallow-sea bottom are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. V. Goncharov, V. Yu. Zaitsev, V. M. Kurtepov, et al., Ocean Acoustic Tomography [in Russian], Inst. Appl. Phys., Nizhny Novgorod (1997).

    Google Scholar 

  2. A. I. Khil’ko, Physical Principles of Sounding Spatially-Localized Inhomogeneities in Layered Waveguieds Using Partially Coherent Fields [in Russian] Dr. Sc. Thesis (Phys. and Math.), Nizhny Novgorod (2006).

  3. A. N. Telegin, ed., Marine Seismo-Prospecting [in Russian], Geoinformmark, Moscow (2004).

    Google Scholar 

  4. A. V. Nikolaev, Sounding of the Earth by Non-explosive Seismic Sources [in Russian], Nauka, Moscow (1981).

    Google Scholar 

  5. V. S. Averbakh, B. N. Bogolyubov, Yu.M. Zaslavsky, et al., Acoust. Phys., 45, No. 1, 1 (1999).

    ADS  Google Scholar 

  6. A. V. Lebedev and A. I. Malekhanov, Radiophys. Quantum Electron., 46, No. 7, 523 (2003).

    Article  ADS  Google Scholar 

  7. V. S. Averbakh, V. V. Artel’ny, B. N. Bogolyubov, et al., in: Fundamental Studies of Oceans and Seas, Vol. 2 [in Russian], Nauka, Moscow (2006), p. 491.

    Google Scholar 

  8. V. A. Lazarev, A. I. Malekhanov, L. R. Merklin et al., in: Physical, Geological, and Biological Studies of Oceans and Seas [in Russian], Nauchnyi Mir, Moscow (2010), p. 300.

    Google Scholar 

  9. A. G. Luchinin and A. I. Khilko, Acoust. Phys., 51, No. 2, 182 (2005).

    Article  ADS  Google Scholar 

  10. A. I. Khilko, A. G. Luchinin, V. G. Burdukovskaya, and I. P. Smirnov, Acoust. Phys., 53, No. 3, 381 (2007).

    Article  ADS  Google Scholar 

  11. A. N. Tikhonov, V. Ya. Arsenin, and A. A. Timonov, Mathematical Problems of Computer Tomography [in Russian], Nauka, Moscow (1987).

    Google Scholar 

  12. I. M. Gel’fand and B. M. Levitan, Izvestia AN SSSR, Ser. Matematika, 15, No. 4, 309 (1951).

    MathSciNet  Google Scholar 

  13. V. A. Marchenko, Doklady AN SSSR, 104, No. 5, 695 (1955).

    MATH  Google Scholar 

  14. L. D. Faddeev, Uspekhi Matem. Nauk, 14, No. 4, 57 (1959).

    MathSciNet  MATH  Google Scholar 

  15. R. Newton, Inverse Schrödinger scattering in Three Dimensions, Springer-Verlag, New York (1989).

    MATH  Google Scholar 

  16. K. P. Gaikovich, Phys. Rev. Lett., 98, No. 8, 183902 (2007).

    Article  ADS  Google Scholar 

  17. P. K. Gaikovich and A. I. Khil’ko, Proc. 11th Sci. Conf. on Radiophysics [in Russian], TALAM, Nizhny Novgorod (2007), p. 185.

    Google Scholar 

  18. L. M. Brekhovskikh, Waves in Layered Media, Academic Press, New York (1960).

    Google Scholar 

  19. P. K. Gaikovich, Proc. 4th Int. Conf. “Ultrawideband and Ultrashort Impulse Signals” (15–19 September, 2008, Sevastopol, Ukraine), IEEE, Sevastopol (2008), p. 189.

    Book  Google Scholar 

  20. K. P. Gaikovich and P. K. Gaikovich, Proc. 10th Anniversary Int. Conf. Trans. Opt. Networks (ICTON 2008, Athens, Greece, June 22–26, 2008), IEEE, Athens (2008), p. 246.

    Google Scholar 

  21. K. P. Gaikovich and P. K. Gaikovich, Inverse Problems, 26, No. 12, 125013 (2010).

    Article  MathSciNet  ADS  Google Scholar 

  22. P. K. Gaikovich and A. I. Khil’ko, Proc. 14th Sci. Conf. on Radiophysics [in Russian], TALAM, Nizhny Novgorod (2010), p. 253.

    Google Scholar 

  23. A. N. Tikhonov, A. V. Goncharsky, V. V. Stepanov, and A. G. Yagola, Regularization Algorithms and A Priori Information [in Russian] Nauka, Moscow (1983).

    Google Scholar 

  24. K. P. Gaikovich, P. K. Gaikovich, Ye. S. Maksimovitch, and V. A. Badeev, Proc. 5th Int. Conf. Ultrawideband and Ultrashort Impulse Signals (6–10 September, 2010, Sevastopol, Ukraine), IEEE, Sevastopol (2010), p. 156.

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Physics of Microstructures of the Russian Academy of Sciences, Nizhny Novgorod, Russia

    P. K. Gaikovich & K. P. Gaikovich

  2. Institute of Applied Physics of the Russian Academy of Sciences, Nizhny Novgorod, Russia

    A. I. Khil’ko

Authors
  1. P. K. Gaikovich
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. I. Khil’ko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. P. Gaikovich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. K. Gaikovich.

Additional information

Translated from Izvestiya Vysshikh Uchebnykh Zavedenii, Radiofizika, Vol. 54, No. 6, pp. 431–443, June 2011.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gaikovich, P.K., Khil’ko, A.I. & Gaikovich, K.P. The method of multifrequency near-field acoustical tomography of bulk inhomogeneities of the sea bottom. Radiophys Quantum El 54, 390–401 (2011). https://doi.org/10.1007/s11141-011-9299-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11141-011-9299-z

Keywords

Search

Navigation