A theoretical analysis of endogenous and exogenous switching costs

Abstract

This paper studies the relation between endogenous and exogenous switching costs. A firm can determine the size of endogenous switching costs, but not the size of exogenous switching costs. This paper develops a game theoretical model to investigate whether these two types of switching costs complement or substitute each other in a firm’s strategy. Our analysis uncovers a substituting relationship, i.e., the equilibrium size of endogenous switching costs should be higher in markets with lower exogenous switching costs. In the equilibrium, the endogenous switching costs cause profit losses to competing firms; the amount of profit loss decreases with the size of exogenous switching costs.

Appendices

Appendix

1.1 Second-period price competition

The firms’ second-period pricing problems are defined as follows:

$$ \matrix{ {p_2^{{A^* }} = \arg \max \pi_2^A = x_1^A\left( {p_2^A - {\tau_A}} \right)x_2^A + x_1^Bp_2^Ax_2^B} \\ {p_2^{{B^* }} = \arg \max \pi = x_1^Ap_2^B\left( {1 - x_2^A} \right) + x_1^B\left( {p_2^B - {\tau_B}} \right)\left( {1 - x_2^B} \right)} \\ }<!end array> $$

where market shares are given below

$$ x_2^A = \frac{1}{2} + \frac{{p_2^B - p_2^A + {\tau_A} + {\tau_0}}}{{2t}}. $$

(A1)

$$ x_2^B = \frac{1}{2} + \frac{{p_2^B - p_2^A - {\tau_B} - {\tau_0}}}{{2t}}. $$

(A2)

Substitute (A1) and (A2) into the optimization problem, we take the first order conditions and solve the second-period prices.

$$ p_2^i = t + x_1^i{\tau_i} + \frac{{2x_1^i - 1}}{3}{\tau_0},\,i = A\;{\mathrm{and}}\;B. $$

(A3)

Substitute the prices (A3) into the market share Eqs. (A1) and (A2), we have

$$ x_2^A = \frac{1}{2} + \frac{1}{{2t}}\left[ {\left( {1 - x_1^A} \right)\left( {{\tau_A} + {\tau_B} + {\tau_0}} \right) + \frac{{1 + x_1^B}}{3}{\tau_0}} \right]. $$

(A4)

$$ x_2^B = \frac{1}{2} - \frac{1}{{2t}}\left[ {x_1^A\left( {{\tau_A} + {\tau_B} + {\tau_0}} \right) + \frac{{1 + x_1^A}}{3}{\tau_0}} \right]. $$

(A5)

Substitute (A3), (A4), and (A5) into firms’ profit functions, we obtain the equilibrium second-period profit.

$$ \pi_2^i = \frac{1}{{2t}}{\left( {t + \frac{{2x_1^i - 1}}{3}{\tau_0}} \right)^2} - \frac{{x_1^Ax_1^B{\tau_i}}}{{2t}}\left( {{\tau_A} + {\tau_B} + 2{\tau_0}} \right),i = A\;{\mathrm{or}}\;B. $$

(A6)

Proof of Proposition 1:

• (1). First, from (A3), we see that a firm’s second-period price $p_2^i$ increases with its own endogenous switching cost τ _i , but is independent of competing firm’s endogenous switching cost. Second, from (A4), we see that a firm’s second-period customer retention rate ($x_2^A$ for firm A) increases with its own (τ _A ) as well as competitor’s endogenous switching cost (τ _B ).

• (2). First, from (A4), we see that a firm’s second-period customer retention rate ($x_2^A$ for firm A) increases with exogenous switching cost (τ ₀). Second, from (A3), we see that a firm’s second-period price $p_2^i$ increases with its exogenous switching cost τ ₀ if the firm’s first-period market share $x_1^i$ is greater than 0.5. When a firm (say, firm A) sets the second-period price, the firm balances between the need to acquire new customers (in segment $x_1^B$) with a low price in order to overcome these consumer’s switching costs τ ₀, and the need for a high price to exploit existing customers (in segment $x_1^A$). The equilibrium price (for firm A) increases with exogenous switching cost (τ ₀) if and only if the need to exploit the existing customers has a larger weight (when $x_1^A$ is larger than $x_1^B$). Q.E.D.

First-period competition

To determine the first-period market shares, we identify the marginal consumers who are indifferent between buying from A and B.

$$ \matrix{ {\left( {v - p_1^A - x_1^At} \right) + \delta \left[ {x_2^A\left( {v - p_2^A + {\tau_A}} \right) - \int_0^{x_2^A} {xtdx} + \left( {1 - x_2^A} \right)\left( {v - p_2^B - {\tau_0}} \right) - \int_{x_2^A}^1 {\left( {1 - x} \right)tdx} } \right]} \hfill \\ { = \left. {\left[ {v - p_1^B - \left( {1 - x_1^A} \right)} \right]t} \right] + \delta \left[ {x_2^B\left( {v - p_2^A - {\tau_0}} \right) - \int_0^{x_2^B} {xtdx} + \left( {1 - x_2^B} \right)\left( {v - p_2^B + {\tau_B}} \right) - \int_{x_2^B}^1 {\left( {1 - x} \right)tdx} } \right],} \hfill \\ }<!end array> $$

(A7)

where $x_2^A$ and $x_2^B$ are given by (A4) and (A5) respectively, and $p_2^A$ and $p_2^B$ are given by (A3). (A7) can be simplified to the following equation:

$$ \matrix{ {H = p_1^A + x_1^At + \delta \left[ {x_2^A\left( {p_2^A - {\tau_A}} \right) + \frac{{x_2^{{A^2}}}}{2}t + \left( {1 - x_2^A} \right)\left( {p_2^B + {\tau_0}} \right) + \frac{{{{\left( {1 - x_2^A} \right)}^2}}}{2}t} \right] - } \hfill \\ {p_1^B - \left( {1 - x_1^A} \right)t - \delta \left[ {x_2^B\left( {p_2^A + {\tau_0}} \right) + \frac{{x_2^{{B^2}}}}{2}t + \left( {1 - x_2^B} \right)\left( {p_2^B - {\tau_B}} \right) + \frac{{{{\left( {1 - x_2^B} \right)}^2}}}{2}t} \right] = 0.} \hfill \\ }<!end array> $$

(A8)

Each firm sets the first-period price and rewards to maximize its total expected profits from two periods. The problem is defined as follows:

$$ \left( {p_1^i,{\tau_i}} \right) = \arg \max {\pi^i} = \pi_1^i + \pi_2^i = p_1^ix_1^i + \pi_2^i\left( {x_1^A} \right) $$

where $x_1^i$ is determined by (A8), 2nd-period profit $\pi_2^i\left( {x_1^A} \right)$ is given by (A6), i = A, B. Note that we assume a firm does not discount future profit. To solve the equilibrium endogenous switching cost and first-period price, we take the first order conditions:

$$ \frac{{\partial {\pi^i}}}{{\partial p_1^i}} = x_1^i + p_1^i\frac{{\partial x_1^i}}{{\partial p_1^i}} + \frac{{\partial \pi_2^i\left( {x_1^A} \right)}}{{\partial p_1^i}} = 0 $$

(A9.1)

$$ \frac{{\partial {\pi^i}}}{{\partial {\tau_i}}} = p_1^i\frac{{\partial x_1^i}}{{\partial {\tau_i}}} + \frac{{\partial \pi_2^i\left( {x_1^A} \right)}}{{\partial {\tau_i}}} = 0 $$

(A9.2)

From (A6), we have

$$ \frac{{\partial \pi_2^i}}{{\partial p_1^i}} = \left[ {\frac{{2{\tau_0}}}{{3t}}\left( {t + \frac{{2x_1^i - 1}}{3}{\tau_0}} \right) - \frac{{{\tau_A} + {\tau_B} + 2{\tau_0}}}{{2t}}{\tau_i}\left( {1 - 2x_1^i} \right)} \right]\frac{{\partial x_1^i}}{{\partial p_1^i}}. $$

(A10.1)

$$ \frac{{\partial \pi_2^i}}{{\partial {\tau_i}}} = \left[ {\frac{{2{\tau_0}}}{{3t}}\left( {t + \frac{{2x_1^i - 1}}{3}{\tau_0}} \right) - \frac{{{\tau_A} + {\tau_B} + 2{\tau_0}}}{{2t}}{\tau_i}\left( {1 - 2x_1^i} \right)} \right]\frac{{\partial x_1^i}}{{\partial {\tau_i}}} - \frac{{{\tau_A} + {\tau_B} + {\tau_i} + 2{\tau_0}}}{{2t}}x_1^i\left( {1 - x_1^i} \right) $$

(A10.2)

To solve the equilibrium first-period prices and endogenous switching costs with Eqs. (A9.1), (A9.2), (A10.1), and (A10.2), we need to obtain $\frac{{\partial x_1^i}}{{\partial p_1^i}}$ and $\frac{{\partial x_1^i}}{{\partial {\tau_i}}}$. A common and direct approach is to solve $x_1^A$ from Eq. (A8), H = 0, and then obtain these derivatives. However, in Eq. (A8), $x_2^A$, $x_2^B$, $p_2^A$, and $p_2^B$ are all functions of $x_1^A$ given by (A3), (A4), and (A5). Since Eq. (A8) involves nonlinear functions of $x_1^A$, the direct approach, which solve $x_1^i$ from (A8) before obtaining first-period equilibrium is quite cumbersome. Instead, it is easier to obtain partial derivatives $\frac{{\partial x_1^i}}{{\partial p_1^i}}$ and $\frac{{\partial x_1^i}}{{\partial {\tau_i}}}$ from Eq. (A8). To ensure that such an approach is valid, one needs to show that the partial derivatives $\frac{{\partial x_1^i}}{{\partial p_1^i}}$ and $\frac{{\partial x_1^i}}{{\partial {\tau_i}}}$ from (A8) are continuous. We prove this property with implicit function theory (Chiang 1984).

Proof with implicit function theory

According to implicit function theory (Chiang 1984, page 204), to ensure that (A8) defines an implicit function ${x_\downarrow }{1^\uparrow }i = h\left( {{p_\downarrow }{1^\uparrow }A,{p_\downarrow }{1^\uparrow }B,{\tau_\downarrow }A,{\tau_\downarrow }B} \right)$ that is continuous and has continuous partial derivatives $\frac{{\partial x_1^i}}{{\partial p_1^i}}$ and $\frac{{\partial x_1^i}}{{\partial {\tau_i}}}$, it is sufficient to show that (a) H has continuous partial derivatives $\frac{{\partial H}}{{\partial x_1^i}}$, $\frac{{\partial H}}{{\partial p_1^i}}$, and $\frac{{\partial H}}{{\partial {\tau_i}}}$, and (b) derivatives $\frac{{\partial H}}{{\partial x_1^i}}$ can be non-zero at some points. Since H is a quadratic function of first-period shares ($x_1^i$), first-period prices ($p_1^i$), and endogenous switching costs τ _i , condition (a) is clearly satisfied. To demonstrate that condition (b) is also satisfied, we examine $\frac{{\partial H}}{{\partial x_1^A}}$.

$$ \begin{array}{*{20}{c}} {\frac{{\partial H}}{{\partial x_{1}^{A}}}=t+\delta \left[ {\frac{{\partial x_{2}^{A}}}{{\partial x_{1}^{A}}}\left( {p_{2}^{A}-{{\tau }_{A}}} \right)+\frac{{\partial p_{2}^{A}}}{{\partial x_{1}^{A}}}x_{2}^{A}+\frac{{\partial x_{2}^{A}}}{{\partial x_{1}^{A}}}x_{2}^{A}t+\left( {1-x_{2}^{A}} \right)\frac{{\partial p_{2}^{B}}}{{\partial x_{1}^{A}}}-\frac{{\partial x_{2}^{A}}}{{\partial x_{1}^{A}}}\left( {p_{2}^{B}+{{\tau }_{0}}} \right)-\left( {1-x_{2}^{A}} \right)t\left( {\partial x_{2}^{A}} \right)/\left( {\partial x_{1}^{A}} \right)} \right]} \\ {-\left\{ {-t+\delta \left[ {\frac{{\partial x_{2}^{B}}}{{\partial x_{1}^{A}}}\left( {p_{2}^{A}+{{\tau }_{0}}} \right)+\frac{{\partial p_{2}^{A}}}{{\partial x_{1}^{A}}}x_{2}^{B}+\frac{{\partial x_{2}^{B}}}{{\partial x_{1}^{A}}}x_{2}^{B}t+\left( {1-x_{2}^{B}} \right)\frac{{\partial p_{2}^{B}}}{{\partial x_{1}^{A}}}-\frac{{\partial x_{2}^{B}}}{{\partial x_{1}^{A}}}\left( {p_{2}^{B}-{{\tau }_{B}}} \right)-\left( {1-x_{2}^{B}} \right)t\left( {\partial x_{2}^{B}} \right)/\left( {\partial x_{1}^{A}} \right)} \right]} \right\}} \\ \end{array} $$

We use (A3), (A4), and (A5) to obtain partial derivatives and substitute into above equation. After further simplification, we obtain

$$ \frac{{\partial H}}{{\partial x_1^A}} = 2t + \frac{\delta }{{2t}}\left( {{\tau_A} + {\tau_B} + \frac{4}{3}{\tau_0}} \right)\left( {{\tau_A} + {\tau_B} + 2{\tau_0}} \right) > 0 $$

Thus, both conditions (a) and (b) for implicit function theory are always satisfied. Q.E.D.

Take first-order derivative on Eq. (A8) with respect to$p_1^A$,

$$ \matrix{ {\frac{{\partial H}}{{\partial p_1^A}} = 1 + \frac{{\partial \xi_1^A}}{{\partial p_1^A}}t + \delta \left[ {\frac{{\partial x_2^A}}{{\partial_1^A}}\left( {p_2^A - {\tau_A}} \right) + x_2^A\frac{{\partial p_2^A}}{{\partial p_1^A}} + x_2^A\frac{{\partial x_2^A}}{{\partial p_1^A}}t + \left( {1 - x_2^A} \right)\frac{{\partial p_2^B}}{{\partial p_1^A}} - \frac{{\partial x_2^A}}{{\partial p_1^A}}\left( {p_2^B + {\tau_0}} \right) - \left( {1 - x_2^A} \right)t\frac{{\partial x_2^A}}{{\partial p_1^A}}} \right]} \hfill \\ { - \left\{ { - \frac{{\partial x_1^A}}{{\partial p_1^A}}t + \delta \left[ {\frac{{\partial x_2^B}}{{\partial p_1^A}}\left( {p_2^A + {\tau_0}} \right) + x_2^B\frac{{\partial p_2^A}}{{\partial p_1^A}} + x_2^B\frac{{\partial x_2^B}}{{\partial p_1^A}}t + \left( {1 - x_2^B} \right)\frac{{\partial p_2^B}}{{\partial p_1^A}} - \frac{{\partial x_2^B}}{{\partial p_1^A}}\left( {p_2^B - {\tau_B}} \right) - \left( {1 - x_2^B} \right)t\frac{{\partial x_2^B}}{{\partial p_1^A}}} \right]} \right\} = 0} \hfill \\ }<!end array> $$

(A11)

From Eqs. (A3), (A4), and (A5), we take first-order derivative with respect to $p_1^A$.

$$ \frac{{\partial p_2^A}}{{\partial p_1^A}} = \left( {{\tau_A} + \frac{2}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial p_1^A}}, $$

(A12.1)

$$ \frac{{\partial p_2^B}}{{\partial p_1^A}} = - \left( {{\tau_B} + \frac{2}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial p_1^A}}, $$

(A12.2)

$$ \frac{{\partial x_2^A}}{{\partial p_1^A}} = - \frac{1}{{2t}}\left[ {\left( {{\tau_A} + {\tau_B} + {\tau_0}} \right) + \frac{1}{3}{\tau_0}} \right]\frac{{\partial x_1^A}}{{\partial p_1^A}} = - \frac{1}{{2t}}\left( {{\tau_A} + {\tau_B} + \frac{4}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial p_1^A}}, $$

(A12.3)

$$ \frac{{\partial x_2^B}}{{\partial p_1^A}} = - \frac{1}{{2t}}\left[ {\left( {{\tau_A} + {\tau_B} + {\tau_0}} \right) + \frac{1}{3}{\tau_0}} \right]\frac{{\partial x_1^A}}{{\partial p_1^A}} = - \frac{1}{{2t}}\left( {{\tau_A} + {\tau_B} + \frac{4}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial p_1^A}}. $$

(A12.4)

Substitute (A12.1) ~ (A12.4) into (A11), we simply the expression and have

$$ \frac{{\partial H}}{{\partial p_1^A}} = 1 + 2t\frac{{\partial x_1^A}}{{\partial p_1^A}} + \delta \frac{{\partial x_1^A}}{{\partial p_1^A}}\left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_A} + {\tau_B} + 2{\tau_0}} \right) = 0 $$

(A13)

From the above equation, we can solve

$$ \frac{{\partial x_1^A}}{{\partial p_1^A}} = \frac{{ - 1}}{{2t + \delta \left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_A} + {\tau_B} + 2{\tau_0}} \right)}} < 0 $$

(A14)

Similarly, we take first-order derivative on Eq. (A8) with respect to τ _A ,

$$ \matrix{ {\frac{{\partial H}}{{\partial {\tau_A}}} = \frac{{\partial x_1^A}}{{\partial {\tau_A}}}t + \delta \left[ {\frac{{\partial x_2^A}}{{\partial {\tau_A}}}\left( {p_2^A - {\tau_A}} \right) + x_1^A\left( {\frac{{\partial p_2^A}}{{\partial {\tau_A}}} - 1} \right) + tx_2^A\frac{{\partial x_2^A}}{{\partial {\tau_A}}} + \left( {1 - x_2^A} \right)\frac{{\partial p_2^B}}{{\partial {\tau_A}}} - \frac{{\partial x_2^A}}{{\partial {\tau_A}}}\left( {p_2^B + {\tau_0}} \right) - \left( {1 - x_2^A} \right)\frac{{\partial x_2^A}}{{\partial {\tau_A}}}} \right]} \hfill \\ { - \left\{ { - \frac{{\partial x_1^A}}{{\partial {\tau_A}}}t + \delta \left[ {\frac{{\partial x_2^B}}{{\partial {\tau_A}}}\left( {p_2^A + {\tau_0}} \right) + x_2^B\frac{{\partial p_2^A}}{{\partial {\tau_A}}} + tx_2^B\frac{{\partial x_2^B}}{{\partial {\tau_A}}} + \left( {1 - x_2^B} \right)\frac{{\partial p_2^B}}{{\partial {\tau_A}}} - \frac{{\partial x_2^B}}{{\partial {\tau_A}}}\left( {p_2^B - {\tau_B}} \right) - \left( {1 - x_2^B} \right)t\frac{{\partial x_2^B}}{{\partial {\tau_A}}}} \right]} \right\} = 0} \hfill \\ }<!end array> $$

(A15)

Again, from Eqs. (A3), (A4), and (A5), we take first-order derivative with respect to τ _A ,

$$ \frac{{\partial p_2^A}}{{\partial {\tau_A}}} = x_1^A + \left( {{\tau_A} + \frac{2}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial {\tau_A}}}, $$

(A16.1)

$$ \frac{{\partial p_2^B}}{{\partial {\tau_A}}} = - \left( {{\tau_B} + \frac{2}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial {\tau_A}}}, $$

(A16.2)

$$ \frac{{\partial x_2^A}}{{\partial {\tau_A}}} = - \frac{1}{{2t}}\left( {{\tau_A} + {\tau_B} + \frac{4}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial {\tau_A}}} + \frac{1}{{2t}}\left( {1 - x_1^A} \right), $$

(A16.3)

$$ \frac{{\partial x_2^B}}{{\partial {\tau_A}}} = - \frac{1}{{2t}}\left( {{\tau_A} + {\tau_B} + \frac{4}{3}{\tau_0}} \right)\frac{{\partial x_1^A}}{{\partial {\tau_A}}} - \frac{1}{{2t}}x_1^A. $$

(A16.4)

Substitute (A16.1) ~ (A16.4) into Eq. (A15), we simplify the expression and have

$$ \frac{{\partial H}}{{\partial H}} = \left[ {2t\frac{{\partial x_1^A}}{{\partial {\tau_A}}} + \delta \frac{{\partial x_1^A}}{{\partial {\tau_A}}}\left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_A} + {\tau_B} + {\tau_0}} \right)} \right] - \frac{\delta }{{2t}}\left[ {t - \left( {2x_1^A - 1} \right)\left( {{\tau_A} + {\tau_B} + \frac{5}{3}{\tau_0}} \right)} \right] = 0 $$

(A17)

From the above equation, we can solve

$$ \frac{{\partial x_1^A}}{{\partial {\tau_A}}} = \frac{{\frac{\delta }{{2t}}\left[ {t - \left( {2x_1^A - 1} \right)\left( {{\tau_A} + {\tau_B} + \frac{5}{3}{\tau_0}} \right)} \right]}}{{{2\mathrm{t} +}\delta \left( {\frac{{{\tau_{\mathrm{A}}} + {\tau_B}}}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}{}} \right)\left( {{\tau_{\mathrm{A}}} + {\tau_{\mathrm{B}}} + 2{\tau_0}} \right)}} $$

(A18)

Substitute (A10.1), (A10.2), (A14), and (A18) into (A9.1) ~ (A9.2), we then apply the symmetry and have

$$ p_1^{{i^* }} = t + \frac{{4{\delta^3}}}{9}t - \frac{2}{9}\left( {3 - {\delta^2}} \right){\tau_0}, $$

(A19)

$$ \tau_i^* = \frac{2}{3}\left( {\delta t - {\tau_0}} \right). $$

(A20)

Substitute (A19) and (A20) into (A3), (A4), and (A5), we obtain 2nd period equilibrium results.

$$ p_2^{{i^* }} = t + \frac{1}{2}\tau_i^* = t + \frac{{\delta t - {\tau_0}}}{3}, $$

(A21)

$$ x_2^{{A^* }} = \frac{1}{2} + \frac{1}{{2t}}\frac{{2\delta t + {\tau_0}}}{3}{ }, $$

(A22)

$$ x_2^{{B^* }} = \frac{1}{2} - \frac{1}{{2t}}\frac{{2\delta t + {\tau_0}}}{3}{ }, $$

(A23)

$$ \pi_2^{{i^* }} = \frac{t}{2} - \frac{{\left( {\delta t - {\tau_0}} \right)\left( {2\delta t + {\tau_0}} \right)}}{{3t}}{ }. $$

(A24)

Proof for Proposition 2

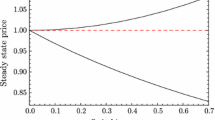
• 2.1. From (A19), it is clear that first-period equilibrium price $p_1^{{i^* }}$ increases with the unit transportation cost (t) but decreases with the exogenous switching cost (τ ₀).

• 2.2. From (A20), it is clear that the equilibrium endogenous switching cost ($\tau_i^*$) increases with unit transportation cost (t) but decreases with the exogenous switching costs (τ ₀). Q.E.D.

2.1 Validate second-order conditions

Here we validate that (A19) and (A20), which are solutions to the first-order conditions (A9.1) and (A9.2), indeed maximize respective firms’ profits. A sufficient condition is negative-definite Hessian, which requires three conditions: $\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}} < 0$, $\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} < 0$, and $\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}}\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} > {\left( {\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^i\partial {\tau_i}}}} \right)^2}$. Next we verify each of these three conditions. For notational convenience, we analyze firm A only. From (A9.1) and (A9.2), we have

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}} = 2\frac{{\partial x_1^i}}{{\partial p_1^i}} + p_1^i\frac{{{\partial^2}x_1^i}}{{\partial p_1^{{i^2}}}} + \frac{{{\partial^2}\pi_2^i\left( {x_1^A} \right)}}{{\partial p_1^{{i^2}}}} $$

(A25.1)

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial {\tau_i}^2}} = p_1^i\frac{{{\partial^2}x_1^i}}{{\partial {\tau_i}^2}} + \frac{{{\partial^2}\pi_2^i\left( {x_1^A} \right)}}{{\partial {\tau_i}^2}} $$

(A25.2)

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial p_1^i\partial {\tau_i}}} = \frac{{\partial x_1^i}}{{\partial {\tau_i}}} + p_1^i\frac{{{\partial^2}x_1^i}}{{\partial p_1^i\partial {\tau_i}}} + \frac{{{\partial^2}\pi_2^i\left( {x_1^A} \right)}}{{\partial p_1^i\partial {\tau_i}}} $$

(A25.3)

From (A13), we can obtain following second-order derivatives,

$$ \frac{{{\partial^2}H}}{{\partial p_1^{{A^2}}}} = 2t\frac{{{\partial^2}x_1^A}}{{\partial p_1^{{A^2}}}} + \delta \frac{{{\partial^2}x_1^A}}{{\partial p_1^{{A^2}}}}\left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_{\mathrm{A}}} + {\tau_{\mathrm{B}}} + {2}{\tau_0}} \right) = 0,\;{\mathrm{and}}\;{\mathrm{then}}\frac{{{\partial^2}x_1^A}}{{\partial p_1^{{A^2}}}} = 0. $$

(A26.1)

$$ \matrix{ {\frac{{{\partial^2}H}}{{\partial p_1^A\partial {\tau_i}}} = 2t\frac{{{\partial^2}x_1^A}}{{\partial p_1^A\partial {\tau_A}}} + \delta \frac{{{\partial^2}x_1^A}}{{\partial p_1^A\partial {\tau_A}}}\left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_{\mathrm{A}}} + {\tau_{\mathrm{B}}} + {2}{\tau_0}} \right)} \hfill \\ { + \delta \frac{{\partial x_1^A}}{{\partial p_1^A}}\left( {\frac{{2{\tau_A} + 2{\tau_B} + 2{\tau_0}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right) = 0.\;\;{\mathrm{Then}}} \hfill \\ {\frac{{{\partial^2}x_1^A}}{{\partial p_1^A\partial {\tau_A}}} = \frac{{\frac{\delta }{t}\left( {{\tau_A} + {\tau_B} + \frac{5}{3}{\tau_0}} \right)}}{{{{\left[ {{2\mathrm{t}} + \delta \left( {\frac{{{\tau_{\mathrm{A}}} + {\tau_B}}}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}} \right)\left( {{\tau_{\mathrm{A}}} + {\tau_{\mathrm{B}}} + 2{\tau_0}} \right)} \right]}^2}}} = \frac{{\frac{\delta }{t}\left( {2\tau_A^* + \frac{5}{3}{\tau_0}} \right)}}{{{{\left[ {{2\mathrm{t}} + {2}\delta \left( {\frac{{\tau_A^* }}{\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}{ ~ }} \right)\left( {\tau_A^* + {\tau_0}} \right)} \right]}^2}}}} \hfill \\ }<!end array> $$

(A26.2)

From (A17),

$$ \matrix{ {\frac{{{\partial^2}H}}{{\partial {\tau_A}^2}}} \hfill &{ = 2t\frac{{{\partial^2}x_1^A}}{{\partial {\tau_A}^2}} + \delta \frac{{{\partial^2}x_1^A}}{{\partial {\tau_A}^2}}\left( {\frac{{{\tau_A} + {\tau_B}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)\left( {{\tau_{\mathrm{A}}} + {\tau_{\mathrm{B}}} + {\tau_0}} \right) + \delta \frac{{\partial x_1^A}}{{\partial {\tau_A}}}\left( {\frac{{2{\tau_A} + 2{\tau_B} + 2{\tau_0}}}{{2t}} + \frac{{2{\tau_0}}}{{3t}}} \right)} \hfill \\ {} \hfill &{ - \frac{\delta }{{2t}}\left( { - 1} \right)\left[ {\left( {2x_1^A - 1} \right) + 2\frac{{\partial x_1^A}}{{\partial {\tau_A}}}\left( {{\tau_A} + {\tau_B} + \frac{5}{3}{\tau_0}} \right)} \right] = 0.\;{\mathrm{Then}\text{,}}} \hfill \\ {} \hfill &{\frac{{{\partial^2}x_1^A}}{{\partial \tau_A^2}} = \frac{{ - \frac{{{\delta^2}}}{t}\left( {2\tau_A^* + \frac{5}{3}{\tau_0}} \right)}}{{{{\left[ {{2\mathrm{t} +}\delta \left( {\frac{{2\tau_{\mathrm{A}}^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}} \right)\left( {{2}\tau_A^* + 2{\tau_0}} \right)} \right]}^2}}}} \hfill \\ }<!end array> $$

(A26.3)

Finally, from (A10.1), we take second-order derivatives, and apply symmetry,

$$ \frac{{{\partial^2}\pi_2^A}}{{\partial p_1^{{A^2}}}} = \left[ {\frac{{4{\tau_0}^2}}{{9t}} + \frac{{\tau_i^* \left( {2\tau_i^* + 2{\tau_0}} \right)}}{t}} \right]{\left( {\frac{{\partial x_1^A}}{{\partial p_1^A}}} \right)^2} + \frac{{2{\tau_0}}}{3}\frac{{{\partial^2}x_1^A}}{{\partial p_1^{{A^2}}}}. $$

(A27.1)

$$ \frac{{{\partial^2}\pi_2^A}}{{\partial p_1^A\partial {\tau_A}}} = \left[ {\frac{{4{\tau_0}^2}}{{9t}} + \frac{{{\tau_0}\left( {2\tau_i^* + 2{\tau_0}} \right)}}{t}} \right]\frac{{\partial x_1^A}}{{\partial p_1^A}}\frac{{\partial x_1^A}}{{\partial {\tau_A}}} + \frac{{2{\tau_0}}}{3}\frac{{{\partial^2}x_1^A}}{{\partial p_1^A\partial {\tau_A}}}. $$

(A27.2)

$$ \frac{{{\partial^2}\pi_2^A}}{{\partial \tau_A^2}} = \left[ {\frac{{4{\tau_0}^2}}{{9t}} + \frac{{\tau_i^* \left( {2\tau_i^* + 2{\tau_0}} \right)}}{t}} \right]{\left( {\frac{{\partial x_1^A}}{{\partial {\tau_A}}}} \right)^2} + \frac{{2{\tau_0}}}{3}\frac{{{\partial^2}x_1^A}}{{\partial \tau_A^2}} - \frac{1}{{4t}}. $$

(A27.3)

Substitute (A14), (A26.1), and (A27.1) into (A25.1), upon simplification, we have

$$ \frac{{{\partial^2}\pi^i}}{{\partial p{{_1^i}^2}}} = \left\{ {\left[ {\frac{{4{\tau_0}^2}}{{9t}} + \frac{{\tau_i^* \left( {2\tau_i^* + 2{\tau_0}} \right)}}{t}} \right]\frac{{\partial x_1^A}}{{\partial p_1^A}} + 2} \right\}\frac{{\partial x_1^A}}{{\partial p_1^A}} $$

From (A14), we know that $\frac{{\partial x_1^A}}{{\partial p_1^A}} < 0$always holds. To see if the first part of expression is always positive, we substitute equilibrium solutions and derive following condition:

$$ \frac{{4\tau_0^2}}{{9t}} + \frac{{\tau_i^* \left( {2\tau_i^* + 2{\tau_0}} \right)}}{t} < 2\left[ {{2\mathrm{t}} + \delta \left( {\frac{{2\tau_{\mathrm{i}}^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}{ }} \right)\left( {{2}\tau_i^* + {\tau_{\mathrm{B}}} + 2{\tau_0}} \right)} \right] $$

which is equivalent to $36{t^2} + 16{\delta^3}{t^2} + 8{\delta^2}t{\tau_0} > 3{\tau_0}^2 + 2{\delta^2}{t^2} - \delta {\tau_0}t$. This condition always holds because t >τ₀ and δ ≤1. Thus, $\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}} < 0.$

Substitute (A26.3) and (A27.3) into (A25.2), upon simplification, we have

$$ \matrix{ {\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} = - \frac{1}{{4t}} - \left\{ {\left( {4\tau_i^* + \frac{{10}}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right) - \left[ {\frac{{2\tau_0^2}}{9} + \tau_i^* \left( {\tau_i^* + {\tau_0}} \right)} \right]} \right\}\frac{{{\delta^2}{M^2}}}{{2t}}} \hfill \\ {{\mathrm{where}}\;\;M = 1/\left[ {{2\mathrm{t}} + \delta \left( {\frac{{2\tau_i^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}{ ~ }} \right)\left( {{2}\tau_i^* + 2{\tau_0}} \right)} \right].} \hfill \\ }<!end array> $$

Upon further simplification, we have

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial {\tau_i}^2}} = - \frac{1}{{4t}} - \left[ {\left( {4t - \tau_i^* - {\tau_0}} \right)\tau_i^* + \left( {\frac{{10}}{3}{\tau_0}t - \frac{{2\tau_0^2}}{9}} \right) + \frac{{4{\delta^2}}}{9}\left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {2\delta t + {\tau_0}} \right)} \right]\frac{{{\delta^2}{M^2}}}{{2t}} $$

Since t >τ₀ and t >τ ^*_i , it is clear that $\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} < 0.$

Finally, substitute (A18), (A26.2), and (A27.2) into (A25.3), upon simplification, we have

$$ \matrix{ {\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^i\partial {\tau_i}}} = \frac{\delta }{2}M + \left\{ {\frac{\delta }{t}\left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right) - \left[ {\frac{{2{\tau_0}^2}}{9} + \tau_i^* \left( {\tau_i^* + {\tau_0}} \right)} \right]} \right\}\frac{{\delta {M^2}}}{t}} \hfill \\ {{\mathrm{where}}\;M = 1/\left[ {{2\mathrm{t}} + \delta \left( {\frac{{2\tau_i^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}} \right)\left( {{2}\tau_i^* + 2{\tau_0}} \right)} \right].} \hfill \\ }<!end array> $$

Upon further simplification, we have

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial {\tau_i}^2}} = - \frac{1}{{4t}} - \left[ {\left( {4t - \tau_i^* - {\tau_0}} \right)\tau_i^* + \left( {\frac{{10}}{3}{\tau_0}t - \frac{{2{\tau_0}^2}}{9}} \right) + \frac{{4{\delta^2}}}{9}\left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {2\delta t + {\tau_0}} \right)} \right]\frac{{{\delta^2}{M^2}}}{{2t}} $$

To verify the third second-order condition $\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}}\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} > {\left( {\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^i\partial {\tau_i}}}} \right)^2}$, we substitute simplified expressions given above. After further simplification, we reduce the condition to

$$ \matrix{ {\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}}\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} - {{\left( {\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^i\partial {\tau_i}}}} \right)}^2}} \hfill &{ = \frac{M}{{2t}} - \frac{{{\delta^2}}}{4}{M^2} - \left[ {\frac{{2\tau_0^2}}{9} + \tau_i^* \left( {\tau_i^* + {\tau_0}} \right)} \right]\frac{{{M^2}}}{{2{t^2}}}} \hfill \\ {} \hfill &{ + \frac{{{\delta^2}{M^3}}}{{{t^2}}}\left[ {t - \left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right)M} \right]\left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right)} \hfill \\ }<!end array> $$

To prove that the above expression is positive, we show that, first, after substituting equilibrium outcomes, the first line of expression is always positive.

$$ \frac{M}{{2t}} - \frac{{{\delta^2}}}{4}{M^2} - \left[ {\frac{{2\tau_0^2}}{9} + \tau_i^* \left( {\tau_i^* + {\tau_0}} \right)} \right]\frac{{{M^2}}}{{2{t^2}}} = {M^2}\left[ {\left( {1 - \frac{{17{\delta^2}}}{{36}} + \frac{2}{9}{\delta^3}} \right) + \frac{{\delta \left( {1 + \delta } \right)}}{t}{\tau_0}} \right] > 0 $$

Second, after substituting equilibrium outcomes, the second line of expression is also positive as

$$ \matrix{ {t - \left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right)M} \\ { = M\left[ {2{t^2} + t\delta \left( {\frac{{2\tau_i^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}} \right)\left( {{2}\tau_i^* + 2{\tau_0}} \right) - \left( {2\tau_i^* + \frac{5}{3}{\tau_0}} \right)\left( {p_1^A + \frac{2}{3}{\tau_0}} \right)} \right]} \\ { = M\left[ {\left( {2 - \frac{4}{3}\delta + \frac{8}{9}{\delta^3} - \frac{{16}}{27}{\delta^{4}}} \right){t^{2}} + \left( {\frac{4}{9}{\delta^{2}} - \frac{1}{3} - \frac{4}{9}{\delta^3}} \right)t{\tau_0} - \frac{2}{{27}}{\delta^2}\tau_0^2} \right]} \\ { = M\left[ {\left( {\frac{4}{3} - \frac{4}{3}\delta + \frac{8}{9}{\delta^3} - \frac{{16}}{27}{\delta^{4}}} \right){t^{2}} + \frac{1}{3}\left( {{{\mathrm{t}}^{2}} - {\mathrm{t}}{\tau_{0}}} \right) + \left( {\frac{4}{9}{\delta^{2}} - \frac{4}{9}{\delta^3}} \right)t{\tau_0} + \left( {\frac{{{t^2}}}{3} - \frac{2}{{27}}{\delta^2}{\tau_0}^2} \right)} \right] > 0} \\ }<!end array> $$

Thus, the second-order conditions are satisfied: $\frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}} < 0,\;\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} < 0$, and

$$ \frac{{{\partial^2}{\pi^i}}}{{\partial p_1^{{i^2}}}}\frac{{{\partial^2}{\pi^i}}}{{\partial \tau_i^2}} > .\;\;{\mathrm{Q}}.{\mathrm{E}}.{\mathrm{D}}. $$

Net effect of reward on second-period equilibrium profit

A firm’s second-period equilibrium profit given by (A6) depends on the firm’s endogenous switching cost in two ways. First, the second-period profit (${\pi_\downarrow }{2^\uparrow }i$) can decrease with τ_i because, given all others the same, the profit is lower when the cost of reward is higher. Second, the second-period profit (${\pi_2^i }$) can increase with τ_i because, given all others the same, profit increase with the first-period market share ($x_1^i$), which is higher when the firm offers more reward. To examine the net effects, we take first-order derivative on $\pi_2^i$ given by (A6) and evaluate it at symmetric outcome ($x_1^{{i^* }} = {{1} \left/ {2} \right.}$).

$$ \matrix{ {\frac{{\partial \pi_2^i\left( {{\tau_i},x_1^i} \right)}}{{\partial {\tau_i}}} = \frac{{\partial \pi_2^i\left( {{\tau_i},x_1^i} \right){ ~ }}}{{\partial {\tau_i}}} + \frac{{\partial \pi_2^i\left( {{\tau_i},x_1^i} \right)}}{{\partial x_1^i}}\frac{{\partial x_1^i}}{{\partial {\tau_i}}}} \hfill \\ { = - \frac{1}{{8t\left( {3\tau_i^* + 2{\tau_0}} \right)}} + \frac{{2{\tau_0}}}{3}\frac{{\partial x_1^i}}{{\partial {\tau_i}}}} \hfill \\ }<!end array> $$

Substitute $\frac{{\partial x_1^i}}{{\partial {\tau_i}}}$ with Eq. (A18), and further simplify the results with equilibrium reward (A20), we have

$$ \matrix{ {\frac{{\partial \pi_2^i\left( {{\tau_i},x_1^i} \right)}}{{\partial {\tau_i}}} = - \frac{\delta }{4} + \frac{{\delta {\tau_0}}}{3}M} \hfill \\ {{\mathrm{where}}\;\;M = 1/\left[ {{2\mathrm{t}} + \delta \left( {\frac{{2\tau_i^* }}{2\mathrm{t}} + \frac{{2{\tau_{0}}}}{3\mathrm{t}}{ ~ }} \right)\left( {{2}\tau_i^* + 2{\tau_0}} \right)} \right].} \hfill \\ }<!end array> $$

Since M <1/(2t) and t >τ ₀ , clearly the net effect $\frac{{\partial \pi_2^i\left( {{\tau_i},x_1^i} \right)}}{{\partial {\tau_i}}} < 0$. Thus, the negative effect of reward cost overweighs the positive effect from a higher market share.

Case 1 for comparison: no endogenous switching costs

As the benchmark case, we derive equilibrium outcomes without endogenous switching costs by imposing τ _A = τ _B  = 0 in the first order conditions. We denote this case by “o”.

$$ p_1^{io} = t + \frac{2}{{3t}}{\tau_0}\left( {\delta {\tau_0} - t} \right) = t - \frac{2}{3}{\tau_0} + \frac{2}{{3t}}\delta {\tau_0}^2, $$

(A28)

$$ p_2^{io} = t, $$

(A29)

$$ x_2^{Ao} = \frac{1}{2} + \frac{{{\tau_0}}}{{2t}}, $$

(A30)

$$ x_2^{Bo} = \frac{1}{{2t}}\left( {t - {\tau_0}} \right), $$

(A31)

$$ \pi_2^{io} = \frac{t}{2},\;\pi_1^{io} = \frac{t}{2} - \frac{1}{3}{\tau_0} + \frac{{\delta \tau_o^2}}{{3t}},{\mathrm{and}}\;{\pi^{io}} = t - \frac{1}{3}{\tau_0} + \frac{1}{{3t}}\delta \tau_o^2 < t $$

(A32)

4.1 Equilibrium properties

Since δτ ₀ <t, from (A28) it is clear that $p_1^{io} < t = p_2^{io}$. Since the equilibrium price with any switching costs is equal to t, exogenous switching costs decrease first-period price.

Now compare (A28) with (A19), we have

$$ p_1^{{i^* }} = t - \frac{2}{3}{\tau_0} + \frac{{4{\delta^3}}}{9}t + \frac{2}{9}{\delta^2}{\tau_0} > p_1^{io} = t - \frac{2}{3}{\tau_0} + \frac{2}{{3t}}\delta \tau_0^2 $$

if and only if $\left( {{2}\delta {\mathrm{t}} + {3}{\tau_{\mathrm{o}}}} \right)\left( {\delta {\mathrm{t}} - {\tau_{\mathrm{o}}}} \right) > 0$, which is always satisfied because δt - τo >0 as assumed. Thus, endogenous switching costs increase first-period price.

Now compare the equilibrium prices in two periods, (A19) and (A21)

$$ p_1^{{i^* }} = t - \frac{2}{3}{\tau_0} + \frac{{4{\delta^3}}}{9}t + \frac{2}{9}{\delta^2}{\tau_0} > p_2^{{i^* }} = t + \frac{1}{2}\tau_i^* = t + \frac{{\delta t - {\tau_0}}}{3}, $$

if and only if ${\delta^{2}}\left( {\delta {\mathrm{t}} - {\tau_{\mathrm{o}}}} \right) > {3}\left( {\delta {\mathrm{t}} + {\tau_{\mathrm{o}}}} \right)\left( {{1} - {\delta^{2}}} \right)$, which will be satisfied with δ is sufficiently close to 1.

We now compute and compare the equilibrium profits,

$$ {\pi^* } = \frac{1}{2}p_1^{{i^* }} + \pi_2^{{i^* }} = \frac{t}{2} - \frac{1}{3}{\tau_0} + \frac{{2{\delta^3}}}{9}t + \frac{1}{9}{\delta^2}{\tau_0} + \frac{t}{2} - \frac{{\left( {\delta t - {\tau_0}} \right)\left( {2\delta t + {\tau_0}} \right)}}{{3t}} < {\pi^{io}} = t - \frac{1}{3}{\tau_0} + \frac{1}{{3t}}\delta {\tau_o}^2, $$

which can be simplified to $\delta \left( {{2}\delta t + {3}{\tau_{\mathrm{o}}}} \right)\left( {\delta {\mathrm{t}} - {\tau_{\mathrm{o}}}} \right) < {3}\left( {{2}\delta {\mathrm{t}} + {\tau_{\mathrm{o}}}} \right)\left( {\delta {\mathrm{t}} - {\tau_{\mathrm{o}}}} \right)$. Clearly, this condition is always satisfied. Thus, equilibrium profit decreases with endogenous switching costs; the larger the loyalty rewards, the greater the loss.

Case 2 for comparison: traditional BBPD

Consider a traditional BBPD model like Chen (1997). In the second period, each firm sets two prices, one for new customers (denoted by $p_{2,n}^i$ for firm i), another for returning customers (denoted by $p_{2,r}^i$ for firm A).

5.1 Second-period price competition

The firms’ second-period pricing problems are defined as follows:

$$ \matrix{ {\left( {p_{2,n}^{{A^* }},p_{2,r}^{{A^* }}} \right) = {\mathrm{argmax}}\;\;\pi_2^A = x_1^A\left( {p_{2,r}^A - {\tau_A}} \right)x_2^A + x_1^Bp_{2,n}^Ax_2^B} \\ {\left( {p_{2,n}^{{B^* }},p_{2,r}^{{B^* }}} \right) = {\mathrm{argmax}}\;\;\pi_2^B = x_1^Ap_{2,n}^B\left( {1 - x_2^A} \right) + x_1^B\left( {p_{2,r}^B - {\tau_B}} \right)\left( {1 - x_2^B} \right)} \\ }<!end array> $$

where market shares are given below

$$ x_2^A = \frac{1}{2} + \frac{{p_{2,n}^B - p_{2,r}^A + {\tau_A} + {\tau_0}}}{{2t}}. $$

(A33)

$$ x_2^B = \frac{1}{2} + \frac{{p_{2,r}^B - p_{2,n}^A - {\tau_B} - {\tau_0}}}{{2t}}. $$

(A34)

Substitute (A33) and (A34) into the optimization problem, we take the first order conditions and solve the second-period prices.

$$ p_{2,r}^i = t + {\tau_i} + \frac{1}{3}{\tau_0},\,i = A\;{\mathrm{and}}\;B. $$

(A35)

$$ p_{2,n}^i = t - \frac{1}{3}{\tau_0},\,i = A\;{\mathrm{and}}\;B. $$

(A36)

Equation (35) shows that, first, endogenous switching cost is perfectly covered in second-period price for returning customers. Thus, under traditional BBPD, endogenous switching cost becomes a meaningless device. Second, the net price for returning customers ($p_{2,r}^i - {\tau_i} = t + {\tau_0}/3$) is always higher than the price for new customers ($p_{2,n}^i = t - {\tau_0}/3$). The difference between two prices (2τ ₀ /3) increases with the size of exogenous switching cost. Substitute the prices (A35) and (A36) into the market share Eqs. (A33) and (A34), we have

$$ x_2^A = \frac{1}{2} + \frac{1}{{6t}}{\tau_0}. $$

(A37)

$$ x_2^B = \frac{1}{2} - \frac{1}{{6t}}{\tau_0}. $$

(A38)

We can then obtain the equilibrium second-period profit.

$$ \pi_2^i = \frac{{x_1^i}}{{2t}}{\left( {t + \frac{1}{3}{\tau_0}} \right)^2} + \frac{{1 - x_1^i}}{{2t}}{\left( {t - \frac{1}{3}{\tau_0}} \right)^2},\,i = A\;{\mathrm{or}}\;B. $$

(A39)

5.2 First-period competition

To determine the first-period market shares, we identify the marginal consumers who are indifferent from buying from A and B.

$$ \matrix{ {\left( {v - p_1^A - x_1^At} \right) + \delta \left[ {x_2^A\left( {v - p_{2,r}^A + {\tau_A}} \right) - \int_0^{x_2^A} {xtdx} + \left( {1 - x_2^A} \right)\left( {v - p_{2,n}^B - {\tau_0}} \right) - \int_{x_2^A}^1 {\left( {1 - x} \right)tdx} } \right] = } \hfill \\ {\left. {\left[ {v - p_1^B - \left( {1 - x_1^A} \right)} \right]t} \right] + \delta \left[ {x_2^B\left( {v - p_{2,n}^A - {\tau_0}} \right) - \int_0^{x_2^B} {xtdx} + \left( {1 - x_2^B} \right)\left( {v - p_{2,r}^B + {\tau_B}} \right) - \int_{x_2^B}^1 {\left( {1 - x} \right)tdx} } \right]} \hfill \\ }<!end array> $$

(A40)

where $x_2^A$ and $x_2^B$ are given by (A37) and (A38) respectively, and second-period prices are given by (A35) and (A36). After simplification, from (A40) we have

$$ x_1^A = \frac{1}{2} + \frac{{p_1^B - p_1^A}}{{2t}}. $$

(A41)

Equation (A41) is very different from the model without price discrimination. This simplified outcome is essentially due to two observations discussed briefly after (A39).

Each firm sets the first-period price to maximize its total expected profits from two periods. Since τ_i is a meaningless device, we no long include it as a decision variable.

$$ p_1^i = \arg \max {\pi^i} = \pi_1^i + \pi_2^i = p_1^ix_1^i + \pi_2^i\left( {x_1^A} \right) $$

where $x_1^i$ is determined by (A41), 2nd-period profit $\pi_2^i\left( {x_1^A} \right)$ is given by (A39), i = A, B. To solve the equilibrium first-period price, we take the first order conditions:

$$ \frac{{\partial {\pi^i}}}{{\partial p_1^i}} = x_1^i + p_1^i\frac{{\partial x_1^i}}{{\partial p_1^i}} + \frac{{\partial \pi_2^i\left( {x_1^A} \right)}}{{\partial p_1^i}} = 0 $$

(A42)

Submitting (A41) and (A39), we have

$$ p_1^{{i^* }} = t - \frac{2}{3}{\tau_0}, $$

(A43)

Total equilibrium profits:

$$ \pi_1^i + \pi_2^i = \frac{1}{2}\left[ {\frac{1}{{2t}}{{\left( {t + \frac{1}{3}{\tau_0}} \right)}^2} + \frac{1}{{2t}}{{\left( {t - \frac{1}{3}{\tau_0}} \right)}^2}} \right] = t - \frac{{{\tau_0}}}{3} + \frac{{\tau_0^2}}{{18t}} $$