Skip to main content
SpringerLink
Log in

Coherent population transfer in multi-level Allen–Eberly models

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

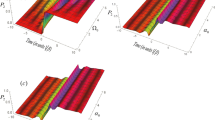
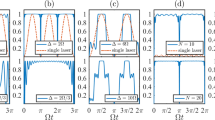
We investigate the solvability of multi-level extensions of the Allen–Eberly model and the population transfer yielded by the corresponding dynamical evolution. We demonstrate that, under a matching condition of the frequency, the driven two-level system and its multi-level extensions possess a stationary-state solution in a canonical representation associated with a unitary transformation. As a consequence, we show that the resulting protocol is able to realize complete population transfer in a nonadiabatic manner. Moreover, we explore the imperfect pulsing process with truncation and display that the nonadiabatic effect in the evolution can lead to suppression to the cutoff error of the protocol.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Weitz, M., Young, B.C., Chu, S.: Atomic interferometer based on adiabatic population transfer. Phys. Rev. Lett. 73, 2563 (1994)

    Article  ADS  Google Scholar 

  2. Goldner, L.S., Gerz, C., Spreeuw, R.J.C., Rolston, S.L., Westbrook, C.I., Phillips, W.D.: Momentum transfer in laser-cooled cesium by adiabatic passage in a light field. Phys. Rev. Lett. 72, 997 (1994)

    Article  ADS  Google Scholar 

  3. Lawall, J., Prentiss, M.: Demonstration of a novel atomic beam splitter. Phys. Rev. Lett. 72, 993 (1994)

    Article  ADS  Google Scholar 

  4. Bergmann, K., Theuer, H., Shore, B.W.: Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003 (1998)

    Article  ADS  Google Scholar 

  5. Vitanov, N.V., Fleischhauer, M., Shore, B.W., Bergmann, K.: Coherent manipulation of atoms and molecules by sequential laser pulses. Adv. Atom Mol. Opt. Phys. 46, 55 (2001)

    Article  ADS  Google Scholar 

  6. Butts, D.L., Kotru, K., Kinast, J.M., Radojevic, A.M., Timmons, B.P., Stoner, R.E.: Efficient broadband raman pulses for large-area atom interferometry. J. Opt. Soc. Am. B. 30, 922 (2013)

    Article  ADS  Google Scholar 

  7. Kumar, P., Sarma, A.K.: Frequency-modulated few-cycle optical-pulse-train-induced controllable ultrafast coherent population oscillations in two-level atomic systems. Phys. Rev. A 87, 025401 (2013)

    Article  ADS  Google Scholar 

  8. Dittmann, P., Pesl, F.P., Martin, J., Coulston, G.W., He, G.Z., Bergmann, K.: The effect of vibrational excitation (\(3\le \nu ^{\prime }\le 19\)) on the reaction \(Na_{2} (\nu ^\prime )+ Cl\rightarrow NaCl + Na^{\ast }\). J. Chem. Phys. 97, 9472 (1992)

    Article  ADS  Google Scholar 

  9. Ohta, Y., Hoki, K., Fujimura, Y.: Theory of stimulated raman adiabatic passage in a degenerated reaction system: application to control of molecular handedness. J. Chem. Phys. 116, 7509 (2002)

    Article  ADS  Google Scholar 

  10. Nitzan, A.: Chemical Dynamics in Condensed Phases. Oxford University Press, Oxford (2006)

    Google Scholar 

  11. Ischenko, A.A., Weber, P.M., Miller, R.J.D.: Capturing chemistry in action with electrons: realization of atomically resolved reaction dynamics. Chem. Rev. 117, 11066 (2017)

    Article  Google Scholar 

  12. Wei, L.F., Johansson, J.R., Cen, L.X., Ashhab, S., Nori, F.: Controllable coherent population transfers in superconducting qubits for quantum computing. Phys. Rev. Lett. 100, 113601 (2008)

    Article  ADS  Google Scholar 

  13. Saffman, M., Walker, T.G., Mølmer, K.: quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313 (2010)

    Article  ADS  Google Scholar 

  14. Sun, G.Z., Wen, X.D., Mao, B., Chen, J., Yu, Y., Wu, P.H., Han, S.Y.: Tunable quantum beam splitters for coherent manipulation of a solid-state tripartite qubit system. Nat. Commun. 1, 51 (2010)

    Article  ADS  Google Scholar 

  15. Imamo\(\bar{{\rm g}}\)lu, A., Awschalom, D.D., Burkard, G., DiVincenzo, D.P., Loss, D., Sherwin, M., Small, A.: quantum information processing using quantum dot spins and cavity QED. Phys. Rev. Lett. 83, 4204 (1999)

  16. Simon, C.M., Belhadj, T., Chatel, B., Amand, T., Renucci, P., Lemaitre, A., Krebs, O., Dalgarno, P.A., Warburton, R.J., Marie, X., Urbaszek, B.: Robust quantum dot exciton generation via adiabatic passage with frequency-swept optical pulses. Phys. Rev. Lett. 106, 166801 (2011)

    Article  ADS  Google Scholar 

  17. Allen, L., Eberly, J.H.: Optical Resonance and Two-Level Atoms. Dover, New York (1975)

    Google Scholar 

  18. Hioe, F.T.: Solution of Bloch equations involving amplitude and frequency modulations. Phys. Rev. A 30, 2100 (1984)

    Article  ADS  Google Scholar 

  19. Carroll, C.E., Hioe, F.T.: Driven three-state model and its analytic solutions. J. Math. Phys. 29, 487 (1988)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Landau, L.D.: Zur theorie der energieubertragung. Phys. Z. Sowjetunion 2, 46 (1932)

    MATH  Google Scholar 

  21. Zener, C.: Non-adiabatic crossing of energy levels. Proc. R. Soc. A. 137, 696 (1932)

    Article  ADS  MATH  Google Scholar 

  22. Rosen, N., Zener, C.: Double Stern–Gerlach experiment and related collision phenomena. Phys. Rev. 40, 502 (1932)

    Article  ADS  MATH  Google Scholar 

  23. Bambini, A., Berman, P.R.: Analytic solutions to the two-state problem for a class of coupling potentials. Phys. Rev. A 23, 2496 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  24. Demkov, Y.N., Kunike, M.: Hypergeometric models of the two-state approximation in the theory of atomic collisions. Vestn. Leningr. Univ. Ser. Fiz. Khim 16, 39 (1969)

    Google Scholar 

  25. Demkov, Y.N.: Charge transfer at small resonance defects. Sov. Phys. JETP 18, 138 (1964)

    Google Scholar 

  26. Nikitin, E.E.: The probability of nonadiabatic transitions in the case of nondivergent terms. Opt. Spectrosc. 13, 431 (1962)

    ADS  Google Scholar 

  27. Nikitin, E.E.: The theory of nonadiabatic transitions: recent development with exponential models. Adv. Quantum Chem. 5, 135 (1970)

    Article  ADS  Google Scholar 

  28. Carroll, C.E., Hioe, F.T.: Generalisation of the Landau–Zener calculation to three levels. J. Phys. A. 19, 3597 (1986)

    MATH  Google Scholar 

  29. Sinitsyn, N.A., Li, F.X.: Solvable multistate model of Landau–Zener transitions in cavity QED. Phys. Rev. A 93, 063859 (2016)

    Article  ADS  Google Scholar 

  30. Li, W., Cen, L.-X.: Dynamical transitions in a modulated Landau–Zener model with finite driving fields. Ann. Phys. 389C, 1 (2018)

    Article  ADS  MathSciNet  Google Scholar 

  31. Barnes, E., Sarma, S.D.: Analytically solvable driven time-dependent two-level quantum systems. Phys. Rev. Lett. 109, 060401 (2012)

    Article  ADS  Google Scholar 

  32. Barnes, E.: Analytically solvable two-level quantum systems and Landau–Zener interferometry. Phys. Rev. A 88, 013818 (2013)

    Article  ADS  Google Scholar 

  33. Yang, G., Li, W., Cen, L.-X.: Nonadiabatic population transfer in a tangent-pulse driven quantum model. Chin. Phys. Lett. 35, 013201 (2018)

    Article  ADS  Google Scholar 

  34. Koppens, F.H.L., Buizert, C., Tielrooij, K.J., Vink, I.T., Nowack, K.C., Meunier, T., Kouwenhoven, L.P., Vandersypen, L.M.K.: Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766 (2006)

    Article  ADS  Google Scholar 

  35. Nowack, K.C., Koppens, F.H.L., Nazarov, Y.V., Vandersypen, L.M.K.: Coherent control of a single electron spin with electric fields. Science 318, 1430 (2007)

    Article  ADS  Google Scholar 

  36. Zhang, J., Shim, J.H., Niemeyer, I., Taniguchi, T., Teraji, T., Abe, H., Onoda, S., Yamamoto, T., Ohshima, T., Isoya, J., Suter, D.: Experimental inplementation of assisted quantum adiabatic passage in a single spin. Phys. Rev. Lett. 110, 240501 (2013)

    Article  ADS  Google Scholar 

  37. Berry, M.V.: Transitionless quantum driving. J. Phys. A 42, 365303 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  38. Chen, X., Lizuain, I., Ruschhaupt, A., Guery-Odelin, D., Muga, J.G.: Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 105, 123003 (2010)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center of Theoretical Physics, College of Physical Science and Technology, Sichuan University, Chengdu, 610065, China

    Wei Li & Li-Xiang Cen

Authors
  1. Wei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li-Xiang Cen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li-Xiang Cen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, W., Cen, LX. Coherent population transfer in multi-level Allen–Eberly models. Quantum Inf Process 17, 97 (2018). https://doi.org/10.1007/s11128-018-1869-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-018-1869-y

Keywords

Search

Navigation