Abstract
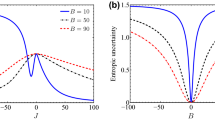
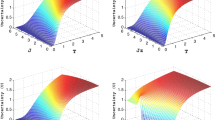
The uncertainty principle is recognized as an elementary ingredient of quantum theory and sets up a significant bound to predict outcome of measurement for a couple of incompatible observables. In this work, we develop dynamical features of quantum memory-assisted entropic uncertainty relations (QMA-EUR) in a two-qubit Heisenberg XXZ spin chain with an inhomogeneous magnetic field. We specifically derive the dynamical evolutions of the entropic uncertainty with respect to the measurement in the Heisenberg XXZ model when spin A is initially correlated with quantum memory B. It has been found that the larger coupling strength \( J \) of the ferromagnetism (\( J < 0 \)) and the anti-ferromagnetism (\( J > 0 \)) chains can effectively degrade the measuring uncertainty. Besides, it turns out that the higher temperature can induce the inflation of the uncertainty because the thermal entanglement becomes relatively weak in this scenario, and there exists a distinct dynamical behavior of the uncertainty when an inhomogeneous magnetic field emerges. With the growing magnetic field \( \left| B \right| \), the variation of the entropic uncertainty will be non-monotonic. Meanwhile, we compare several different optimized bounds existing with the initial bound proposed by Berta et al. and consequently conclude Adabi et al.’s result is optimal. Moreover, we also investigate the mixedness of the system of interest, dramatically associated with the uncertainty. Remarkably, we put forward a possible physical interpretation to explain the evolutionary phenomenon of the uncertainty. Finally, we take advantage of a local filtering operation to steer the magnitude of the uncertainty. Therefore, our explorations may shed light on the entropic uncertainty under the Heisenberg XXZ model and hence be of importance to quantum precision measurement over solid state-based quantum information processing.









Similar content being viewed by others
References
Heisenberg, W.: Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172 (1927)
Robertson, H.P.: Violation of Heisenberg’s uncertainty principle. Phys. Rev. 34, 163 (1929)
Kennard, E.H.: Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 44, 326 (1927)
Deutsch, D.: Uncertainty in quantum measurements. Phys. Rev. Lett. 50, 631–633 (1983)
Maassen, H., Uffink, J.B.M.: Generalized entropic uncertainty relations. Phys. Rev. Lett. 60, 1103 (1988)
Kraus, K.: Complementary observables and uncertainty relations. Phys. Rev. D 35, 3070 (1987)
Maccone, L., Pati, A.K.: Stronger uncertainty relations for the sum of variances. Phys. Rev. Lett. 113, 260401 (2014)
Wang, K.K., Zhan, X., Bian, Z.H., Li, J., Zhang, Y.S., Xue, P.: Experimental investigation of the stronger uncertainty relations for all incompatible observables. Phys. Rev. A 93, 052108 (2016)
Renes, J.M., Boileau, J.C.: Conjectured strong complementary information tradeoff. Phys. Rev. Lett. 103, 020402 (2009)
Berta, M., Christandl, M., Colbeck, R., Renes, J.M., Renner, R.: The uncertainty principle in the presence of quantum memory. Nat. Phys. 6, 659–662 (2010)
Prevedel, R., Hamel, D.R., Colbeck, R., Fisher, K., Resch, K.J.: Experimental investigation of the uncertainty principle in the presence of quantum memory and its application to witnessing entanglement. Nat. Phys. 7, 757–761 (2011)
Li, C.F., Xu, J.S., Xu, X.Y., Li, K., Guo, G.C.: Experimental investigation of the entanglement-assisted entropic uncertainty principle. Nat. Phys. 7, 752–756 (2011)
Nielson, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2002)
Pati, A.K., Wilde, M.M., Devi, A.U., Rajagopal, A.K., Sudha, : Quantum discord and classical correlation can tighten the uncertainty principle in the presence of quantum memory. Phys. Rev. A 86, 042105 (2012)
Coles, P.J., Piani, M.: Improved entropic uncertainty relations and information exclusion relations. Phys. Rev. A 89, 022112 (2014)
Adabi, F., Salimi, S., Haseli, S.: Tightening the entropic uncertainty bound in the presence of quantum memory. Phys. Rev. A 93, 062123 (2016)
Pramanik, T., Mal, S., Majumdar, A.S.: Lower bound of quantum uncertainty from extractable classical information. Quantum Inf. Process. 15, 981–999 (2016)
Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)
Hu, M. L., Hu, X. Y., Wang, J. C., Peng, Y., Zhang, Y. R and Fan, H.: Quantum coherence and quantum correlations. arXiv: 1703.01852 (2017)
Hu, M.L., Fan, H.: Upper bound and shareability of quantum discord based on entropic uncertainty relations. Phys. Rev. A 88, 014105 (2013)
Dupuis, F., Fawzi, O., Wehner, S.: Entanglement sampling and applications. IEEE Trans. Inf. Theory 61, 1093 (2015)
Koenig, R., Wehner, S., Wullschleger, J.: Unconditional security from noisy quantum storage. IEEE Trans. Inf. Theory 58, 1962–1984 (2012)
Vallone, G., Marangon, D.G., Tomasin, M., Villoresi, P.: Quantum randomness certified by the uncertainty principle. Phys. Rev. A 90, 052327 (2014)
Cerf, N.J., Bourennane, M., Karlsson, A., Gisin, N.: Security of quantum key distribution using d-level systems. Phys. Rev. Lett. 88, 127902 (2002)
Grosshans, F., Cerf, N.J.: Continuous-variable quantum cryptography is secure against non-Gaussian attacks. Phys. Rev. Lett. 92, 047905 (2004)
Jarzyna, M., Demkowicz-Dobrzański, R.: True precision limits in quantum metrology. New J. Phys. 17, 013010 (2015)
Jia, L.J., Tian, Z.H., Jing, J.L.: Entropic uncertainty relation in de Sitter space. Ann. Phys. 353, 37–47 (2015)
Zou, H.M., Fang, M.F., Yang, B.Y., Guo, Y.N., He, W., Zhang, S.Y.: The quantum entropic uncertainty relation and entanglement witness in the two-atom system coupling with the non-Markovian environments. Phys. Scr. 89, 115101 (2014)
Yao, C.M., Chen, Z.H., Ma, Z.H., Severini, S., Serafini, A.: Entanglement and discord assisted entropic uncertainty relations under decoherence. Sci. China Phys. Mech. Astron. 57, 1703–1711 (2014)
Zhang, Y.L., Fang, M.F., Kang, G.D., Zhou, Q.P.: Reducing quantum-memory-assisted entropic uncertainty by weak measurement and weak measurement reversal. Int. J. Quantum Inf. 13, 1550037 (2015)
Xu, Z.Y., Yang, W.L., Feng, M.: Quantum-memory-assisted entropic uncertainty relation under noise. Phys. Rev. A 86, 012113 (2012)
Wang, D., Ming, F., Huang, A.J., Sun, W.Y., Shi, J.D., Ye, L.: Exploration of quantum-memory-assisted entropic uncertainty relations in a noninertial frame. Laser Phys. Lett. 14, 055205 (2017)
Feng, J., Zhang, Y.Z., Gould, M.D., Fan, H.: Entropic uncertainty relations under the relativistic motion. Phys. Lett. B 726, 527–532 (2013)
Huang, A.J., Shi, J.D., Wang, D., Ye, L.: Steering quantum-memory-assisted entropic uncertainty under unital and nonunital noises via filtering operations. Quantum Inf. Process. 16, 46 (2017)
Zheng, X., Zhang, G.F.: The effects of mixedness and entanglement on the properties of the entropic uncertainty in Heisenberg model with Dzyaloshinski–Moriya interaction. Quantum Inf. Process. 16, 1 (2017)
Huang, A.J., Wang, D., Wang, J.M., Shi, J.D., Sun, W.Y., Ye, L.: Exploring entropic uncertainty relation in the Heisenberg XX model with inhomogeneous magnetic field. Quantum Inf. Process. 16, 204 (2017)
Asoudeh, M., Karimipour, V.: Thermal entanglement of spins in an inhomogeneous magnetic field. Phys. Rev. A 71, 022308 (2005)
Liang, Q.: Quantum correlations in a two-qubit Heisenberg XX model under intrinsic decoherence. Commun. Theor. Phys. 60, 391 (2013)
Zhang, G.F., Li, S.S.: Thermal entanglement in a two-qubit Heisenberg XXZ spin chain under an inhomogeneous magnetic field. Phys. Rev. A 72, 034302 (2005)
Wang, D., Ming, F., Huang, A.J., Sun, W.Y., Ye, L.: Entropic uncertainty for spin-1/2 XXX chains in the presence of inhomogeneous magnetic fields and its steering via weak measurement reversals. Laser Phys. Lett. 14, 095204 (2017)
Sumana, K., Ajoy, S., Amit, B., Debasis, S.: Effect of local filtering on freezing phenomena of quantum correlation. Quantum Inf. Process. 14, 2517–2533 (2015)
Michael, S., Ali, A.K.: Defeating entanglement sudden death by a single local filtering. Phys. Rev. A 86, 032304 (2012)
Peters, N.A., Wei, T.C., Kwiat, P.G.: Mixed-state sensitivity of several quantum-information benchmarks. Phys. Rev. A 70, 052309 (2004)
Singh, U., Bera, M.N., Dhar, H.S., Pati, A.K.: Maximally coherent mixed states: complementarity between maximal coherence and mixedness. Phys. Rev. A 91, 052115 (2015)
Wang, S.C., Yu, Z.W., Wang, X.B.: Protecting quantum states from decoherence of finite temperature using weak measurement. Phys. Rev. A 89, 022318 (2014)
Zhang, S.Y., Fang, M.F., Yu, M.: Controlling of entropic uncertainty in qubits system under the generalized amplitude damping channel via weak measurements. Int. J. Theor. Phys. 55, 1824–1832 (2016)
Zhang, S.Y., Fang, M.F., Zhang, Y.L., Guo, Y.N., Zhao, Y.J., Tang, W.W.: Reduction of entropic uncertainty in entangled qubits system by local PT-symmetric operation. Chin. Phys. B 24, 090304 (2015)
Flavien, H., Marco, T.Q., Joseph, B., Nicolas, B.: Genuine hidden quantum nonlocality. Phys. Rev. Lett. 111, 160402 (2013)
Sun, Q.Q., Al-Amri, M., Davidovich, L., Suhail Zubairy, M.: Reversing entanglement change by a weak measurement. Phys. Rev. A 82, 052323 (2010)
Acknowledgements
This work was supported by the National Science Foundation of China under Grant Nos. 61601002 and 11575001, Anhui Provincial Natural Science Foundation (Grant No. 1508085QF139), and the fund from CAS Key Laboratory of Quantum Information (Grant No. KQI201701).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ming, F., Wang, D., Shi, WN. et al. Entropic uncertainty relations in the Heisenberg XXZ model and its controlling via filtering operations. Quantum Inf Process 17, 89 (2018). https://doi.org/10.1007/s11128-018-1857-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-018-1857-2