Capacity of a quantum memory channel correlated by matrix product states

Abstract

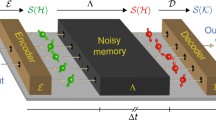
We study the capacity of a quantum channel where channel acts like controlled phase gate with the control being provided by a one-dimensional quantum spin chain environment. Due to the correlations in the spin chain, we get a quantum channel with memory. We derive formulas for the quantum capacity of this channel when the spin state is a matrix product state. Particularly, we derive exact formulas for the capacity of the quantum memory channel when the environment state is the ground state of the AKLT model and the Majumdar–Ghosh model. We find that the behavior of the capacity for the range of the parameters is analytic.

A Proof of Lemma 3

The lemma can be easily verified for the cases when $n=2$, and $n=3$. So we prove for the case $n \ge 4$ with $\{A_1,A_2\}$ as in Eq. (8).

Proof for values

The proof is based on the observation that, for $n \ge 4$,

$$\begin{aligned}&\{O_1O_2 \cdots O_nO_n^\dagger \cdots O_2^\dagger O_1^\dagger : O_i \in \{A_1, A_2\}, 1 \le i \le n \} \\&\quad =\left\{ \text {diag}(0,0,0), \text {diag}\Big (g^{\Big \lfloor \frac{n}{2} \Big \rfloor }, 0, 0\Big ), \right. \\&\qquad \text {diag}\Big (g^i(1-g)^{\Big \lfloor \frac{n}{2}\Big \rfloor - i}, 0, 0\Big ): 1 \le i \le \Big \lfloor \frac{n}{2} \Big \rfloor - 1,\\&\qquad \text {diag}\Big ((1-g)^{\Big \lfloor \frac{n}{2}\Big \rfloor }, g^{\Big \lceil \frac{n}{2} \Big \rceil }, 0\Big ), \\&\qquad \text {diag}\Big (0, g^i(1-g)^{\Big \lceil \frac{n}{2}\Big \rceil - i}, 0\Big ): 1 \le i \le \Big \lceil \frac{n}{2} \Big \rceil - 1,\\&\qquad \text {diag}\Big (0, (1-g)^{\Big \lceil \frac{n}{2} \Big \rceil }, g^{\Big \lfloor \frac{n}{2}\Big \rfloor }\Big ), \\&\qquad \text {diag}\Big (0,0,g^{\Big \lfloor \frac{n}{2}\Big \rfloor - i}(1-g)^i\Big ): 1 \le i \le \Big \lfloor \frac{n}{2}\Big \rfloor - 1, \\&\qquad \left. \text {diag}\Big (0,0, (1-g)^{\Big \lfloor \frac{n}{2}\Big \rfloor }\Big ) \right\} \end{aligned}$$

Consequently, for $n \ge 4$,

$$\begin{aligned}&\{\text {Tr}(\rho O_1\cdots O_nO_n^\dagger \cdots O_1^\dagger ): O_i \in \{A_1, A_2\}, 1 \le i \le n \} \\&\quad =\left\{ 0, \displaystyle \frac{(1-g)g^{\left\lfloor \frac{n}{2}\right\rfloor }}{2}, \displaystyle \frac{g^i(1-g)^{\left\lfloor \frac{n}{2}\right\rfloor - i + 1}}{2}: 1 \le i \le \left\lfloor \frac{n}{2} \right\rfloor - 1,\right. \\&\qquad \displaystyle \frac{(1-g)^{\left\lfloor \frac{n}{2}\right\rfloor + 1} +g^{\left\lceil \frac{n}{2}\right\rceil }}{2}, \displaystyle \frac{g^i(1-g)^{\left\lceil \frac{n}{2}\right\rceil - i}}{2}: 1 \le i \le \left\lceil \frac{n}{2} \right\rceil - 1, \\&\qquad \displaystyle \frac{(1-g)^{\left\lceil \frac{n}{2}\right\rceil }+g^{ \left\lfloor \frac{n}{2}\right\rfloor + 1}}{2}, \displaystyle \frac{g^{ \left\lfloor \frac{n}{2}\right\rfloor - i +1}(1-g)^i}{2}: 1 \le i \le \left\lfloor \frac{n}{2}\right\rfloor - 1, \\&\left. \qquad \displaystyle \frac{g(1-g)^{\left\lfloor \frac{n}{2}\right\rfloor }}{2} \right\} \end{aligned}$$

Now, the nonzero values for $\text {Tr}(\rho O_1 \cdots O_nO_n^\dagger \cdots O_1^\dagger )$ can be inferred as stated in the lemma. The validity of the observation can be established by mathematical induction on n. For $n=4$, the observation can be verified explicitly. Now, assuming that the observation is valid for an arbitrary integer $k \ge 4$, we prove that the observation holds for $k+1$. Let

$$\begin{aligned} \begin{array}{lll} Z_k &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} (0,0,0), \\ B_k &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( g^{\left\lfloor \frac{k}{2} \right\rfloor }, 0, 0\right) , \\ C_k(i) &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( g^i(1-g)^{\left\lfloor \frac{k}{2}\right\rfloor - i}, 0, 0\right) , \\ D_k &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( (1-g)^{\left\lfloor \frac{k}{2}\right\rfloor }\right) , \\ E_k(i) &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( 0, g^i(1-g)^{\left\lceil \frac{k}{2}\right\rceil - i}, 0\right) , \\ F_k &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( 0, (1-g)^{\left\lceil \frac{k}{2} \right\rceil }, g^{\left\lfloor \frac{k}{2}\right\rfloor }\right) , \\ G_k(i) &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( 0,0,g^{\left\lfloor \frac{k}{2}\right\rfloor - i}(1-g)^i\right) , \\ \hbox {and}\; H_k &{} \hbox {denote} &{} \text {diag}_{_{k \times k}} \left( 0,0, (1-g)^{\left\lfloor \frac{k}{2}\right\rfloor }\right) . \end{array} \end{aligned}$$

By induction hypothesis

$$\begin{aligned}&\left\{ O_1 \cdots O_kO_k^\dagger \cdots O_1^\dagger : O_i \in \{A_1, A_2\}, 1 \le i \le k\right\} \\&\quad =\left\{ Z_k, B_k, C_k(i): 1 \le i \le \left\lfloor \frac{k}{2} \right\rfloor - 1,D_k,\right. \\&\left. \qquad E_k(i):1 \le i \le \left\lceil \frac{k}{2} \right\rceil - 1, F_k, G_k(i):1 \le i \le \left\lfloor \frac{k}{2}\right\rfloor - 1, H_k\right\} . \end{aligned}$$

So,

$$\begin{aligned}&\{A_1O_1 \cdots O_kO_k^\dagger \cdots O_1^\dagger A_1^\dagger , A_2O_1 \cdots O_kO_k^\dagger \cdots O_1^\dagger A_2^\dagger :\\&\qquad O_i \in \{A_1, A_2\}, 1 \le i \le k \} \\&\quad =\left\{ A_1Z_kA_1^\dagger , A_1B_kA_1^\dagger , A_1C_k(i)A_1^\dagger : 1 \le i \le \left\lfloor \frac{k}{2} \right\rfloor - 1, \right. \\&\qquad A_1D_kA_1^\dagger , A_1E_k(i)A_1^\dagger :1 \le i \le \left\lceil \frac{k}{2} \right\rceil - 1, \\&\qquad A_1F_kA_1^\dagger , A_1G_k(i)A_1^\dagger :1 \le i \le \left\lfloor \frac{k}{2}\right\rfloor - 1, \\&\qquad A_1H_kA_1^\dagger , A_2Z_kA_2^\dagger , A_2B_kA_2^\dagger , A_2C_k(i)A_2^\dagger : 1 \le i \le \left\lfloor \frac{k}{2} \right\rfloor - 1, \\&\qquad A_2D_kA_2^\dagger , A_2E_k(i)A_2^\dagger :1 \le i \le \left\lceil \frac{k}{2} \right\rceil - 1, \\&\left. \qquad A_2F_kA_2^\dagger , A_2G_k(i)A_2^\dagger :1 \le i \le \left\lfloor \frac{k}{2}\right\rfloor - 1, A_2H_kA_2^\dagger \right\} \end{aligned}$$

Now, since

$$\begin{aligned}&A_1Z_kA_1^{\dagger }, A_1B_kA_1^{\dagger }, A_1C_k(i)A_1^{\dagger },A_2Z_kA_2^{\dagger }, A_2G_k(i)A_2^{\dagger }, \nonumber \\&A_2H_kA_2^{\dagger } \quad \text {are all}\, Z_{k+1},\, \text {for} \, 1 \le i \le \left\lfloor \frac{k}{2} \right\rfloor -1, \end{aligned}$$

(25)

$$\begin{aligned}&A_1D_kA_1^{\dagger } = B_{k+1}, \end{aligned}$$

(26)

$$\begin{aligned}&A_1 E_k(i) A_1^{\dagger } = C_{k+1}(i)\, \text {for}\, 1 \le i \le \left\lfloor \frac{k+1}{2} \right\rfloor - 1, \end{aligned}$$

(27)

$$\begin{aligned}&A_1 F_k A_1^{\dagger } = D_{k+1},\end{aligned}$$

(28)

$$\begin{aligned}&A_1H_kA_1^{\dagger }, A_2C_k(1)A_2^{\dagger }\, \text {are} \, E_{k+1}(1),\end{aligned}$$

(29)

$$\begin{aligned}&A_1G_k \left( \left\lfloor \frac{k}{2} \right\rfloor -i+1\right) A_1^{\dagger }, A_2 C_k(i)A_2^{\dagger } \, \text {are}\, E_{k+1}(i)\nonumber \\&\text {for} \, 2 \le i \le \left\lceil \frac{k+1}{2} \right\rceil -2, \end{aligned}$$

(30)

$$\begin{aligned}&A_1G_k(1)A_1^{\dagger }, A_2B_kA_2^{\dagger }\, \text {are}\, E_{k+1}\left( \left\lceil \frac{k+1}{2} \right\rceil - 1\right) ,\end{aligned}$$

(31)

$$\begin{aligned}&A_2 D_kA_2^{\dagger } = F_{k+1},\end{aligned}$$

(32)

$$\begin{aligned}&A_2 E_k(i)A_2^{\dagger }\; \hbox {is}\; G_{k+1}(i)\, \text {for}\, 1 \le i \le \left\lfloor \frac{k+1}{2} \right\rfloor - 1, \end{aligned}$$

(33)

$$\begin{aligned}&A_2F_kA_2^{\dagger } = H_{k+1} \end{aligned}$$

(34)

we get

$$\begin{aligned}&\{A_1O_1 \cdots O_kO_k^\dagger \cdots O_1^\dagger A_1^\dagger , A_2O_1 \cdots O_kO_k^\dagger \cdots O_1^\dagger A_2^\dagger : \\&\qquad O_i \in \{A_1, A_2\}, 1 \le i \le k \} \\&\quad =\left\{ Z_{k+1}, B_{k+1}, C_{k+1}(i): 1 \le i \le \left\lfloor \frac{k+1}{2} \right\rfloor - 1, D_{k+1}, \right. \\&\qquad E_{k+1}: 1 \le i \le \left\lceil \frac{k+1}{2} \right\rceil -1,F_{k+1}, \\&\left. \qquad G_{k+1}: 1 \le i \le \left\lfloor \frac{k+1}{2} \right\rfloor - 1, H_{k+1} \right\} \end{aligned}$$

Proof of multiplicity

Let $z_n$, $b_n$, $c_n(i)$, $d_n$, $e_n(i)$, $f_n$, $g_n(i)$, and $h_n$ denote the multiplicity of $Z_n$, $B_n$, $C_n(i)$, $D_n$, $E_n(i)$, $F_n$, $G_n(i)$, and $H_n$, respectively, in $\{ O_1 O_2 \cdots O_n O_n^{\dagger } O_{n-1}^{\dagger } \cdots O_1^{\dagger }: O_i \in \{A_1, A_2\}, 1 \le i \le n\}$. From Eqs. (25)–(34), we obtain the following recurrence relations: For $n\ge 5$,

$$\begin{aligned} z_{n+1}= & {} 2z_n+b_n+\sum _{i=1}^{\left\lfloor \frac{n}{2} \right\rfloor -1} c_n(i) + \sum _{i=1}^{\left\lfloor \frac{n}{2} \right\rfloor -1} g_n(i) + h_n \\ b_{n+1}= & {} d_n \\ c_{n+1}(i)= & {} e_n(i): 1 \le i \le \left\lfloor \frac{n+1}{2} \right\rfloor - 1, \\ d_{n+1}= & {} f_n, \\ e_{n+1}(1)= & {} h_n + c_n(1), \\ e_{n+1}(i)= & {} g_n\left( \left\lfloor \frac{n}{2} \right\rfloor - i +1\right) +c_n(i): 2 \le i \le \left\lceil \frac{n+1}{2} \right\rceil - 2, \\ e_{n+1}\left( \left\lceil \frac{n+1}{2} \right\rceil - 1\right)= & {} g_n(1) + b_n, \\ f_{n+1}= & {} d_n, \\ g_{n+1}(i)= & {} e_n\left( \left\lceil \frac{n}{2} \right\rceil - i\right) : 1 \le i \le \left\lfloor \frac{n+1}{2} \right\rfloor - 1, \\ h_{n+1}= & {} f_n \end{aligned}$$

with initial conditions

$$\begin{aligned} z_4= & {} 6, b_4 = 1, c_4(1)=2, d_4 = 1, e_4 (1) = 1, \\ f_4= & {} 1, g_4(1)=2,h_4 = 1 \end{aligned}$$

Solving the above recurrences with the given initial conditions results in

$$\begin{aligned} z_n= & {} 2^n - 2^{\lfloor \frac{n}{2} \rfloor + 1} - 2^{\left\lceil \frac{n}{2} \right\rceil } + 2, n \ge 4 \\ b_n= & {} 1, n \ge 4 \\ c_n(i)= & {} \left( \begin{array}{cc} \left\lfloor \frac{n}{2} \right\rfloor \\ i \end{array} \right) : 1 \le i \le \left\lfloor \frac{n}{2} \right\rfloor - 1, n \ge 4 \\ d_n= & {} 1, n \ge 4 \\ e_n(i)= & {} \left( \begin{array}{cc} \left\lceil \frac{n}{2} \right\rceil \\ i \end{array} \right) : 1 \le i \le \left\lceil \frac{n}{2} \right\rceil - 1, n \ge 4 \\ f_n= & {} 1, n \ge 4 \\ g_n(i)= & {} \left( \begin{array}{cc} \left\lfloor \frac{n}{2} \right\rfloor \\ i \end{array} \right) : 1 \le i \le \left\lfloor \frac{n}{2} \right\rfloor - 1, n \ge 4 \\ h_n= & {} 1, n \ge 4 \end{aligned}$$

Now that we have identified the distinct values along with multiplicities for

$$\begin{aligned} O_1 \cdots O_nO_n^\dagger \cdots O_1^\dagger \, \text {with} \, O_i \in \{A_1, A_2\} \, \text {and}\, 1 \le i \le n \end{aligned}$$

we can consider the cases of n being odd or even to conclude the lemma.