Skip to main content
SpringerLink
Log in

A one-way quantum amplifier for long-distance quantum communication

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

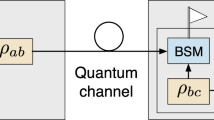
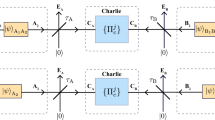
In this paper, a model for single photon amplification based on cluster-state quantum computation is proposed. A rescaling of the probability amplitudes of a deteriorated qubit in favor of the one-photon component will define the amplifier’s gain. Unlike the heralded quantum amplifiers, the probabilistic success of the whole process will not depend on the successful detection of a heralding signal. Instead, the whole procedure will rely upon a single-qubit measurement, which is simpler compared to any two-qubit interaction gate in the heralded quantum amplifiers. The proposed model can be used as a qubit protector against propagation losses in long-distance quantum communication networks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Notes

  1. This requirement is specific to our analysis, where in general the transfer matrix is Hermitian.

  2. Where \(\vert {\psi }\rangle \) = \(\alpha \vert {0}\rangle +\beta \vert {1}\rangle \) is an arbitrary qubit state.

  3. The \(\frac{1}{\sqrt{2}}\)factor will be taken care of when normalizing the whole state.

  4. This indistinguishability is crucial to the whole amplification process.

  5. Since the detection of one photon in either \(\hat{d_{+}}\) or \(\hat{d_{-}}\) leads to Eq. 7, the probability to successfully produce that state is given by twice its norm.

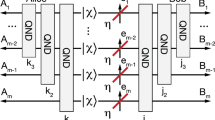
  6. All of the probability amplitudes can be adjusted as a function of the linear optical elements that will be used during experimentation. This will be clear in Sect. 3.

  7. \(\vert {+}\rangle \) and \(\vert {-}\rangle \) are the eigenstates of the Pauli-X operator with eigenvalues +1, −1, respectively.

  8. The Pauli group is the group of the famous Pauli \(\sigma \) operators.

  9. Where X is the Pauli \(\sigma _{x}, \sigma _{x} \vert {+}\rangle =\vert {+}\rangle \).

  10. \(\rho ^{\prime }={U}\rho {U^{\dagger }}\).

  11. Where this step to be included in the ‘polarization encoding’ block in our diagrams from now on.

  12. This simple encoder consists of: an input in a general polarization state to be encoded, a PBS and an entanglement resource in the state \(\vert {\phi ^{+}}\rangle \). At the PBS, the general input state will be mixed with one member of the entangled resource, and then the detection of exactly one photon at the output of the PBS means that the other two are exiting the device.

  13. Again this can be put in the standard form by applying a Hadamard to qubits 1 and 4.

References

  1. Preskill, J.: Physics 219. Lecture notes. http://www.theory.caltech.edu/people/preskill/ph229/

  2. Caves, C.M.: Quantum limits on noise in linear amplifiers. Phys. Rev. D 26, 1817 (1982)

    Article  ADS  Google Scholar 

  3. Wootters, W.K., Zurek, W.H.: A single quantum cannot be cloned. Nature 299, 802–803 (1982)

    Article  ADS  Google Scholar 

  4. Ralph, T.C., Lund, A.P.: Nondeterministic noiseless linear amplification of quantum systems. In: Lvovsky, A. (eds.) Quantum Communication Measurement and Computing Proceedings of 9th International Conference, pp. 155–160 (2009)

  5. Osorio, C.I., Bruno, N., Sangouard, N., Zbinden, H., Gisin, N., Thew, R.T.: Heralded photon amplification for quantum communication. Phys. Rev. A 86, 023815 (2012)

    Article  ADS  Google Scholar 

  6. Jeffers, J.: Nondeterministic amplifier for two-photon superpositions. Phys. Rev. A 82, 063828 (2010)

    Article  ADS  Google Scholar 

  7. Meyer-Scott, E., Bula, M., Bartkiewicz, K., Ĉernoch, A., Soubusta, J., Jennewein, T., Lemr, K.: Entanglement-based linear-optical qubit amplifier. Phys. Rev. A 88, 012327 (2013)

    Article  ADS  Google Scholar 

  8. Knill, E., Laflamme, R., Milburn, G.J.: A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001)

    Article  ADS  MATH  Google Scholar 

  9. Raussendorf, R., Briegel, H.J.: A one-way quantum computer. Phys. Rev. Lett. 86, 5188 (2001)

    Article  ADS  Google Scholar 

  10. Browne, D.E., Briegel, H. J.: One-way quantum computation—a tutorial introduction. arXiv:quant-ph/0603226

  11. Nielsen, M. A.: Cluster-state quantum computation. arXiv:quant-ph/0504097

  12. Nielsen, M.A., Chuang, I.L.: Quantum computation and quantum information, 1st edn. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  13. Horodecki, R., Horodecki, P., Horodecki, M., Horodecki, K.: Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Bennett, C.H., Brassard, G., Mermin, N.D.: Quantum cryptography without Bells theorem. Phys. Rev. Lett. 68, 557 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Ekert, A.K.: Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 67, 661 (1991)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Zbinden, H., Bechmann-Pasquinucci, H., Gisin, N., Ribordy, G.: Quantum cryptography. Appl. Phys. B 67, 743748 (1998)

    Article  Google Scholar 

  17. Gisin, N., Ribordy, G., Tittel, W., Zbinden, H.: Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002)

    Article  ADS  Google Scholar 

  18. Bennett, C.H., Brassard, G., Crpeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  19. Bouwmeester, D., Pan, J.-W., Mattle, K., Eibl, M., Weinfurter, H., Zeilinger, A.: Experimental quantum teleportation. Nature 390, 575–579 (1997)

    Article  ADS  Google Scholar 

  20. Duan, L.-M., Lukin, M.D., Cirac, J.I., Zoller, P.: Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001)

    Article  ADS  Google Scholar 

  21. Sangouard, N., Simon, C., de Riedmatten, H., Gisin, N.: Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33 (2011)

    Article  ADS  Google Scholar 

  22. Azuma, K., Tamaki, K., Lo, H.-K.: All-photonic quantum repeaters. Nat. Commun. 6, Article number: 6787 (2015)

  23. Gerry, C., Knight, P.: Introductory Quantum Optics, Chapter 6, 1st edn. Cambridge University Press, Cambridge (2005)

    Google Scholar 

  24. Barnum, H., Nielsen, M.A., Schumacher, B.: Information transmission through a noisy quantum channel. Phys. Rev. A 57, 4153 (1997)

    Article  ADS  Google Scholar 

  25. Gupta, V.P., Mandayam, P., Sunder, V.S.: The Functional Analysis of Quantum Information Theory. Springer, Berlin (2015)

    Book  MATH  Google Scholar 

  26. Christensen, O.: Functions, Spaces, and Expansions. Birkhuser Mathematics, Basel (2010)

    Book  MATH  Google Scholar 

  27. Desurvire, E.: A three-dimensional quantum vacuum-noise/signal beamsplitter model for nonideal linear optical amplifiers. Opt. Fiber Technol. 5(1), 81 (1999)

    ADS  Google Scholar 

  28. Ketterle, W.: 8.422 Atomic and Optical Physics II, Spring 2013 (Massachusetts Institute of Technology: MIT OpenCourseWare). http://ocw.mit.edu/courses/physics/8-422-atomic-and-optical-physics-ii-spring-2013/

  29. Lambropoulos, P., Petrosyan, D.: Fundamentals of Quantum Optics and Quantum Information. Springer, Berlin (2007)

    Google Scholar 

  30. Agarwal, G.S.: Quantum Optics, Chapter 10, 1st edn. Cambridge University Press, Cambridge (2012)

    Book  Google Scholar 

  31. Deutsch, I.H.: Physics 581 Quantum Optics II. http://info.phys.unm.edu/~ideutsch/Classes/Phys581F16/index.htm

  32. Eastin, B., Flammia, S.T.: Q-circuit tutorial. arXiv:quant-ph/0406003v2 (This diagram was plotted using this tool)

  33. Kok, P., Lovett, B.W.: Introduction to Optical Quantum Information Processing. Cambridge University Press, Cambridge (2010)

    Book  MATH  Google Scholar 

  34. Gottesman, D.: The Heisenberg Representation of Quantum Computers. arXiv:quant-ph/9807006

  35. Gottesman, D.: Stabilizer Codes and Quantum Error Correction. arXiv:quant-ph/9705052

  36. Korzh, B., et al.: Provably secure and practical quantum key distribution over 307 km of optical fibre. Nat. Photon. 9, 163168 (2015)

    Article  Google Scholar 

  37. Jozsa, R.: Fidelity for mixed quantum states. J. Mod. Opt. 41(12), 2315–2323 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. Gottesman, D.: Quantum Error Correction QECC2007. Course http://perimeterinstitute.ca/personal/dgottesman/QECC2007/

  39. Vazirani, U.: CS294-2: quantum computation. Lecture notes. https://people.eecs.berkeley.edu/~vazirani/s09quantum.html

  40. Chao-Yang, L., Zhou, X.-Q., Ghne, O., Gao, W.-B., Zhang, J., Yuan, Z.-S., Goebe, A., Yang, T., Pan, J.-W.: Experimental entanglement of six photons in graph states. Nat. Phys. 3, 91–95 (2007)

    Article  Google Scholar 

  41. Browne, D.E., Rudolph, T.: Resource-efficient linear optical quantum computation. Phys. Rev. Lett. 95, 010501 (2005)

    Article  ADS  Google Scholar 

  42. Pittman, T.B., Jacobs, B.C., Franson, J.D.: Probabilistic Quantum Encoder for Single-Photon Qubits. arXiv:quant-ph/0312097

  43. Walther, P., Resch, K.J., Rudolph, T., Schenck, E., Weinfurter, H., Vedral, V., Aspelmeyer, M., Zeilinger, A.: Experimental one-way quantum computing. Nature 434, 169–176 (2005)

    Article  ADS  Google Scholar 

  44. Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423, 623–656 (1948)

Download references

Author information

Authors and Affiliations

  1. Faculty of Engineering, Ain-Shams University, Cairo, Egypt

    Hany Elemy

Authors
  1. Hany Elemy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hany Elemy.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Elemy, H. A one-way quantum amplifier for long-distance quantum communication. Quantum Inf Process 16, 134 (2017). https://doi.org/10.1007/s11128-017-1582-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1582-2

Keywords

Search

Navigation