Abstract
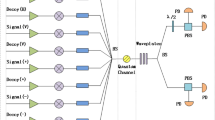
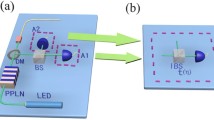
We present a new scheme on implementing the passive quantum key distribution with thermal distributed parametric down-conversion source. In this scheme, only one-intensity decoy state is employed, but we can achieve very precise estimation on the single-photon-pulse contribution by utilizing those built-in decoy states. Moreover, we compare the new scheme with other practical methods, i.e., the standard three-intensity decoy-state BB84 protocol using either weak coherent states or parametric down-conversion source. Through numerical simulations, we demonstrate that our new scheme can drastically improve both the secure transmission distance and the key generation rate.



Similar content being viewed by others
References
Ekert, A.K.: Quantum cryptography based on Bell\(^{^{\prime }}\)s theorem. Phys. Rev. Lett. 67, 611 (1991)
Shor, P.W., Preskill, J.: Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441 (2000)
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, pp. 175–179. IEEE, New York (1984)
Huttner, B., Imoto, N., Gisin, N., Mor, T.: Quantum cryptography with coherent states. Phys. Rev. A. 51, 1863 (1995)
Brassard, G., Lütkenhaus, N., Mor, T., Sanders, B.C.: Limitations on practical quantum cryptography. Phys. Rev. Lett. 85, 1330 (2000)
Hwang, W.Y.: Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003)
Wang, X.-B.: Beating the Photon-Number-Splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005)
Lo, H.K., Ma, X.-F., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005)
Wang, X.-B., Peng, C.-Z., Zhang, J., Yang, L., Pan, J.W.: General theory of decoy-state quantum cryptography with source errors. Phys. Rev. A. 77, 042311 (2008)
Wang, X.-B., Yang, L., Peng, C.-Z., Pan, J.W.: Decoy-state quantum key distribution with both source errors and statistical fluctuations. New J. Phys. 11, 075006 (2009)
Wang, Q., Wang, X.-B., Guo, G.-C.: Practical decoy-state method in quantum key distribution with a heralded single-photon source. Phys. Rev. A. 75, 012312 (2007)
Wang, Q., Chen, W., Xavier, G., Swillo, M., Zhang, T., Sauge, S., Tengner, M., Han, Z.-F., Guo, G.-C., Karlsson, A.: Experimental decoy-state quantum key distribution with a sub-Poissionian heralded single-photon source. Phys. Rev. Lett. 100, 090501 (2008)
Wang, Q., Karlsson, A.: Performance enhancement of a decoy-state quantum key distribution using a conditionally prepared down-conversion source in the Poisson distribution. Phys. Rev. A. 76, 014309 (2007)
Wang, Q., Wang, X.-B., Björk, G., Karlsson, A.: Improved practical decoy state method in quantum key distribution with parametric downconversion source. Europhys. Lett. 79, 40001 (2007)
Ma, X.-F., Qi, B., Zhao, Y., Lo, H.K.: Practical decoy state for quantum key distribution. Phys. Rev. A. 72, 012326 (2005)
Wang, X.-B.: Decoy-state protocol for quantum cryptography with four different intensities of coherent light. Phys. Rev. A. 72, 012322 (2005)
Adachi, Y., Yamamoto, Y., Masato, K., Imoto, N.: Simple and efficient quantum key distribution with parametric down-conversion. Phys. Rev. Lett. 99, 180503 (2007)
Curty, M., Ma, X.-F., Qi, B., Moroder, T.: Passive decoy-state quantum key distribution with practical light sources. Phys. Rev. A. 81, 022310 (2010)
Zambra, G., Andreoni, A., Bondani, M., Gramegna, M., Genovese, M., Brida, G., Rossi, A., Paris, M.G.: Experimental reconstruction of photon statistics without photon counting. Phys. Rev. Lett. 95, 063602 (2005)
Chekhova, M., Kulik, S.: Physical Foundations of Quantum Electronics. World Scientific Publishing Company, Singapore (2011)
Brida, G., Degiovanni, I.-P., Genovese, M., Piacentini, F., Traina, P., Della Frera, A., Tosi, A., Bahgat Shehata, A., Scarcella, C., Gulinatti, A., Ghioni, M., Polyakov, S.-V., Migdall, A., Giudice, A.: An extremely low-noise heralded single-photon source: a breakthrough for quantum technologies. Appl. Phys. Lett. 101, 221112 (2012)
Ngah, L.A., Alibart, O., Labonté, L., D’Auria, V., Tanzilli, S.: Ultra-fast heralded single photon source based on telecom technology. Laser Photonics Rev. 9(2), L1 (2015)
Yurke, B., Potasek, M.: Obtainment of thermal noise from a pure quantum state. Phys. Rev. A. 36, 3464 (1987)
Lütkenhaus, N.: Security against individual attacks for realistic quantum key distribution. Phys. Rev. A. 61, 052304 (2000)
Zhou, Y.-H., Yu, Z.-W., Wang, X.-B.: Tightened estimation can improve the key rate of measurement-device-independent quantum key distribution by more than 100%. Phys. Rev. A. 89, 052325 (2014)
Zhang, C.-H., Luo, S.-L., Guo, G.-C., Wang, Q.: Approaching the ideal quantum key distribution with two-intensity decoy states. Phys. Rev. A. 92, 022332 (2015)
Acknowledgements
We gratefully acknowledge the financial support from the National Natural Science Foundation of China through Grants Nos. 11274178, 61475197, and 61590932, the Natural Science Foundation of the Jiangsu Higher Education Institutions through Grant No. 15KJA120002, the Outstanding Youth Project of Jiangsu Province through Grant No. BK20150039, and the Priority Academic Program Development of Jiangsu Higher Education Institutions through Grant No. YX002001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wei, J., Zhang, CH. & Wang, Q. New passive decoy-state quantum key distribution with thermal distributed parametric down-conversion source. Quantum Inf Process 16, 50 (2017). https://doi.org/10.1007/s11128-016-1510-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11128-016-1510-x