Skip to main content
SpringerLink
Log in

Deterministic transmission of an arbitrary single-photon polarization state through bit-flip error channel

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

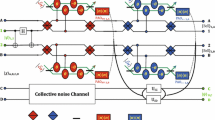
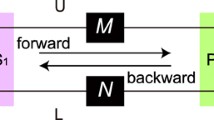
We present two error-tolerance transmission protocols of a single-photon polarization state when bit-flip error is taken into account. For achieving the transmission target of the single-photon state, the first protocol needs to encode it to a nonmaximally entangled Bell state. Exploiting the interaction of the polarization entanglement with spatial entanglement between two photons, its success probability is 100 %. Different from the first protocol, the second one utilizes the idea of teleportation with an auxiliary Bell state. By performing quantum nondemolition measurement to analyze the parity, conventional measurement, and unitary transformation operations, the success probability of the second protocol is approximately unity. Furthermore, the second protocol can be generalized to the error-tolerance transmission of an arbitrary mixed state or the distribution of an arbitrary multi-photon entangled state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Shor, P.W.: Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52(4), R2493–R2496 (1995)

    Article  ADS  Google Scholar 

  2. Steane, A.M.: Error correcting codes in quantum theory. Phys. Rev. Lett. 77(5), 793–797 (1996)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  3. Bennett, C.H., DiVincenzo, D.P., Smolin, J.A., Wootters, W.K.: Mixed-state entanglement and quantum error correction. Phys. Rev. A 54(5), 3824–3851 (1996)

    Article  MathSciNet  ADS  Google Scholar 

  4. Laflamme, R., Miquel, C., Paz, J.P., Zurek, W.H.: Perfect quantum error correcting code. Phys. Rev. Lett. 77(1), 198–201 (1996)

    Article  ADS  Google Scholar 

  5. Bouwmeester, D.: Bit-flip-error rejection in optical quantum communication. Phys. Rev. A 63(3), 040301 (2001)

    Article  ADS  Google Scholar 

  6. Kalamidas, D.: Feasible quantum error detection with linear optics. Phys. Lett. A 321(2), 87–93 (2004)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  7. Wang, X.-B.: Quantum error-rejection code with spontaneous parametric down-conversion. Phys. Rev. A 69(2), 022320 (2004)

    Article  ADS  Google Scholar 

  8. Yamamoto, T., Shimamura, J., Özdemir, S.K., Koashi, M., Imoto, N.: Faithful qubit distribution assisted by one additional qubit against collective noise. Phys. Rev. Lett. 95(4), 040503 (2005)

    Article  ADS  Google Scholar 

  9. Kalamidas, D.: Single-photon quantum error rejection and correction with linear optics. Phys. Lett. A 343(5), 331–335 (2005)

    Article  ADS  MATH  Google Scholar 

  10. Li, X.-H., Deng, F.-G., Zhou, H.-Y.: Faithful qubit transmission against collective noise without ancillary qubits. Appl. Phys. Lett. 91(14), 144101 (2007)

    Article  ADS  Google Scholar 

  11. Li, X.-H., Zhao, B.-K., Sheng, Y.-B., Deng, F.-G., Zhou, H.-Y.: Efficient faithful qubit transmission with frequency degree of freedom. Opt. Commun. 282(19), 4025–4027 (2009)

    Article  ADS  Google Scholar 

  12. Deng, F.-G., Li, X.-H., Zhou, H.-Y.: Passively self-error-rejecting qubit transmission over a collective-noise channel. Quantum Inf. Comput. 11, 0913–0924 (2011)

    MathSciNet  MATH  Google Scholar 

  13. Salemian, S., Mohammadnejad, S.: An error-free protocol for quantum entanglement distribution in long-distance quantum communication. Chin. Sci. Bull. 56(7), 618–625 (2011)

    Article  Google Scholar 

  14. Pan, J.-W., Chen, Z.-B., Lu, C.-Y., Weinfurter, H., Zeilinger, A., Zukowski, M.: Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84(2), 777–838 (2012)

    Article  ADS  Google Scholar 

  15. Zanardi, P., Rasetti, M.: Noiseless quantum codes. Phys. Rev. Lett. 79(17), 3306–3309 (1997)

    Article  ADS  Google Scholar 

  16. Boileau, J.-C., Gottesman, D., Laflamme, R., Poulin, D., Spekkens, R.: Robust polarization-based quantum key distribution over a collective-noise channel. Phys. Rev. Lett. 92(1), 017901 (2004)

    Article  ADS  Google Scholar 

  17. Wang, X.-B.: Fault tolerant quantum key distribution protocol with collective random unitary noise. Phys. Rev. A 72(5), 050304(R) (2005)

    Article  ADS  Google Scholar 

  18. Aolita, L., Walborn, S.: Quantum communication without alignment using multiple-qubit single-photon states. Phys. Rev. Lett. 98(10), 100501 (2007)

    Article  ADS  Google Scholar 

  19. Li, X.-H., Deng, F.-G., Zhou, H.-Y.: Efficient quantum key distribution over a collective noise channel. Phys. Rev. A 78(2), 022321 (2008)

    Article  ADS  Google Scholar 

  20. Sheng, Y.-B., Deng, F.-G.: Efficient quantum entanglement distribution over an arbitrary collective-noise channel. Phys. Rev. A 81(4), 042332 (2010)

    Article  ADS  Google Scholar 

  21. Li, X.-H.: Deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 82(4), 044304 (2010)

    Article  ADS  Google Scholar 

  22. Deng, F.-G.: One-step error correction for multipartite polarization entanglement. Phys. Rev. A 83(6), 062316 (2011)

    Article  ADS  Google Scholar 

  23. Dong, L., Xiu, X.-M., Gao, Y.-J., Yi, X.X.: Controlled quantum key distribution with three-photon polarization-entangled states via the collective noise channel. J. Exp. Theor. Phys. 113(4), 583–591 (2011)

    Article  ADS  Google Scholar 

  24. Yang, Y.-G., Teng, Y.-W., Chai, H.-P., Wen, Q.-Y.: Fault-tolerant quantum secret sharing against collective noise. Phys. Scr. 83(2), 25003 (2011)

    Article  MATH  Google Scholar 

  25. Andersson, E., Curty, M., Jex, I.: Experimentally realizable quantum comparison of coherent states and its applications. Phys. Rev. A 74(2), 022304 (2006)

    Article  ADS  Google Scholar 

  26. He, B., Ren, Y., Bergou, J.: Creation of high-quality long-distance entanglement with flexible resources. Phys. Rev. A 79(5), 052323 (2009)

    Article  ADS  Google Scholar 

  27. Turchette, Q.A., Hood, C.J., Lange, W., Mabuchi, H., Kimble, H.J.: Measurement of conditional phase shifts for quantum logic. Phys. Rev. Lett. 75(25), 4710–4713 (1995)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  28. Rauschenbeutel, A., Nogues, G., Osnaghi, S., Bertet, P., Brune, M., Raimond, J., Haroche, S.: Coherent operation of a tunable quantum phase gate in cavity QED. Phys. Rev. Lett. 83(24), 5166–5169 (1999)

    Article  ADS  Google Scholar 

  29. Koashi, M., Yamamoto, T., Imoto, N.: Probabilistic manipulation of entangled photons. Phys. Rev. A 63(1), 030301(R) (2001)

    Article  ADS  Google Scholar 

  30. Knill, E., Laflamme, R., Milburn, G.J.: A scheme for efficient quantum computation with linear optics. Nature 409(6816), 46–52 (2001)

    Article  ADS  MATH  Google Scholar 

  31. Yi, X.X., Su, X.H., You, L.: Conditional quantum phase gate between two 3-state atoms. Phys. Rev. Lett. 90(9), 097902 (2003)

    Article  ADS  Google Scholar 

  32. Knill, E.: Bounds on the probability of success of postselected nonlinear sign shifts implemented with linear optics. Phys. Rev. A 68(6), 064303 (2003)

    Article  ADS  Google Scholar 

  33. Xiu, X.-M., Dong, L., Shen, H.-Z., Gao, Y.-J., Yi, X.X.: Construction scheme of a two-photon polarization controlled arbitrary phase gate mediated by weak cross-phase modulation. J. Opt. Soc. Am. B 30(3), 589–597 (2013)

    Article  ADS  Google Scholar 

  34. Pittman, T., Jacobs, B., Franson, J.: Probabilistic quantum logic operations using polarizing beam splitters. Phys. Rev. A 64(6), 062311 (2001)

    Article  ADS  Google Scholar 

  35. Pittman, T., Fitch, M., Jacobs, B., Franson, J.: Experimental controlled-NOT logic gate for single photons in the coincidence basis. Phys. Rev. A 68(3), 032316 (2003)

    Article  ADS  Google Scholar 

  36. Scheel, S., Munro, W., Eisert, J., Nemoto, K., Kok, P.: Feed-forward and its role in conditional linear optical quantum dynamics. Phys. Rev. A 73(3), 034301 (2006)

    Article  ADS  Google Scholar 

  37. Kok, P., Nemoto, K., Ralph, T.C., Dowling, J.P., Milburn, G.J.: Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79(1), 135–174 (2007)

    Article  ADS  Google Scholar 

  38. Nemoto, K., Munro, W.J.: Nearly deterministic linear optical controlled-NOT gate. Phys. Rev. Lett. 93(25), 250502 (2004)

    Article  ADS  Google Scholar 

  39. Lin, Q., Li, J.: Quantum control gates with weak cross-Kerr nonlinearity. Phys. Rev. A 79(2), 022301 (2009)

    Article  ADS  Google Scholar 

  40. Wang, M.-F., Jiang, N.-Q., Jin, Q.-L., Zheng, Y.-Z.: Continuous-variable controlled-Z gate using an atomic ensemble. Phys. Rev. A 83(6), 062339 (2011)

    Article  ADS  Google Scholar 

  41. Xiu, X.-M., Dong, L., Gao, Y.-J., Yi, X.X.: Nearly deterministic controlled-not gate with weak cross-kerr nonlinearities. Quantum Info. Comput. 12(1–2), 0159–0170 (2012)

    MathSciNet  MATH  Google Scholar 

  42. Barrett, S.D., Kok, P., Nemoto, K., Beausoleil, R.G., Munro, W.J., Spiller, T.P.: Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities. Phys. Rev. A 71(6), 060302 (2005)

    Article  ADS  Google Scholar 

  43. Munro, W.J., Nemoto, K., Spiller, T.P.: Weak nonlinearities: a new route to optical quantum computation. N. J. Phys. 7(1), 137 (2005)

    Article  Google Scholar 

  44. Guo, Q., Bai, J., Cheng, L.-Y., Shao, X.-Q., Wang, H.-F., Zhang, S.: Simplified optical quantum-information processing via weak cross-Kerr nonlinearities. Phys. Rev. A 83(5), 054303 (2011)

    Article  ADS  Google Scholar 

  45. Wang, X.-W., Zhang, D.-Y., Tang, S.-Q., Xie, L.-J., Wang, Z.-Y., Kuang, L.-M.: Photonic two-qubit parity gate with tiny cross-Kerr nonlinearity. Phys. Rev. A 85(5), 052326 (2012)

    Article  ADS  Google Scholar 

  46. Xiu, X.-M., Dong, L., Gao, Y.-J., Yi, X.X.: Quantum key distribution with Einstein–Podolsky–Rosen pairs associated with weak cross-Kerr nonlinearities. J. Opt. Soc. Am. B 29(10), 2869–2874 (2012)

    Article  ADS  Google Scholar 

  47. Wang, X.-W., Tang, S.-Q., Xie, L.-J., Zhang, D.-Y.: Nondestructive two-photon parity detector with near unity efficiency. Opt. Commun. 296, 153–157 (2013)

    Article  ADS  Google Scholar 

  48. Munro, W.J., Nemoto, K., Beausoleil, R.G., Spiller, T.P.: High-efficiency quantum-nondemolition single-photon-number-resolving detector. Phys. Rev. A 71(3), 033819 (2005)

    Article  ADS  Google Scholar 

  49. Fleischhauer, M., Imamoglu, A., Marangos, J.P.: Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77(2), 633–673 (2005)

    Article  ADS  Google Scholar 

  50. Chen, Y.-F., Wang, C.-Y., Wang, S.-H., Yu, I.: Low-light-level cross-phase-modulation based on stored light pulses. Phys. Rev. Lett. 96(4), 043603 (2006)

    Article  ADS  Google Scholar 

  51. Wang, Z.-B., Marzlin, K.-P., Sanders, B.C.: Large cross-phase modulation between slow copropagating weak pulses in \(^{87}\)Rb. Phys. Rev. Lett. 97(6), 063901 (2006)

    Article  ADS  Google Scholar 

  52. Sheng, Y.-B., Deng, F.-G., Zhou, H.-Y.: Efficient polarization-entanglement purification based on parametric down-conversion sources with cross-Kerr nonlinearity. Phys. Rev. A 77(4), 042308 (2008)

    Article  ADS  Google Scholar 

  53. Sheng, Y.-B., Deng, F.-G., Zhou, H.-Y.: Nonlocal entanglement concentration scheme for partially entangled multipartite systems with nonlinear optics. Phys. Rev. A 77(6), 062325 (2008)

    Article  ADS  Google Scholar 

  54. Lin, Q., He, B.: Single-photon logic gates using minimal resources. Phys. Rev. A 80(10), 042310 (2009)

    Article  ADS  Google Scholar 

  55. Sheng, Y.-B., Deng, F.-G.: Deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement. Phys. Rev. A 81(3), 032307 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  56. Lin, Q., He, B.: Efficient generation of universal two-dimensional cluster states with hybrid systems. Phys. Rev. A 82(8), 022331 (2010)

    Article  ADS  Google Scholar 

  57. Bing, H., Ren, Y.-H., Bergou, J.: Universal entangler with photon pairs in arbitrary states. J. Phys. B At. Mol. Opt. Phys. 43(2), 025502 (2010)

    Article  ADS  Google Scholar 

  58. He, B., MacRae, A., Han, Y., Lvovsky, A., Simon, C.: Transverse multimode effects on the performance of photon-photon gates. Phys. Rev. 83(2), 022312 (2011)

    Article  ADS  Google Scholar 

  59. Lo, H.-Y., Chen, Y.-C., Chen, H.-C., Chen, J.-X., Chen, Y.-C., Yu, I.A., Chen, Y.-F.: Electromagnetically-induced-transparency-based cross-phase-modulation at attojoule levels. Phys. Rev. A 83(4), 041804(R) (2011)

    Article  ADS  Google Scholar 

  60. He, B., Scherer, A.: Continuous-mode effects and photon-photon phase gate performance. Phys. Rev. A 85(3), 033814 (2012)

    Article  ADS  Google Scholar 

  61. Siomau, M., Kamli, A.A., Moiseev, S.A., Sanders, B.C.: Entanglement creation with negative index metamaterials. Phys. Rev. A 85(5), 050303(R) (2012)

    Article  ADS  Google Scholar 

  62. Sheng, Y.-B., Zhou, L., Zhao, S.-M., Zheng, B.-Y.: Efficient single-photon-assisted entanglement concentration for partially entangled photon pairs. Phys. Rev. A 85(1), 012307 (2012)

    Article  ADS  Google Scholar 

  63. Sheng, Y.-B., Zhou, L., Zhao, S.-M.: Efficient two-step entanglement concentration for arbitrary W states. Phys. Rev. A 85(4), 042302 (2012)

    Article  ADS  Google Scholar 

  64. Zhou, L., Sheng, Y.-B., Cheng, W.-W., Gong, L.-Y., Zhao, S.-M.: Efficient entanglement concentration for arbitrary less-entangled NOON states. Quantum Info. Process. 12(2), 1307–1320 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  65. Sheng, Y.-B., Zhou, L., Long, G.-L.: Hybrid entanglement purification for quantum repeaters. Phys. Rev. A 88(2), 022302 (2013)

    Article  ADS  Google Scholar 

  66. Sheng, Y.-B., Zhou, L.: Quantum entanglement concentration based on nonlinear optics for quantum communications. Entropy 15(5), 1776–1820 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  67. Zhou, L., Sheng, Y.-B., Cheng, W.-W., Gong, L.-Y., Zhao, S.-M.: Efficient entanglement concentration for arbitrary single-photon multimode W state. J. Opt. Soc. Am. B 30(1), 71 (2013)

    Article  ADS  Google Scholar 

  68. Xia, Y., Lu, M., Song, J., Lu, P-m, Song, H-s: Effective protocol for preparation of four-photon polarization-entangled decoherence-free states with cross-Kerr nonlinearity. J. Opt. Soc. Am. B 30(2), 421–428 (2013)

    Article  ADS  Google Scholar 

  69. Xiu, X.-M., Dong, L., Shen, H.-Z., Gao, Y.-J., Yi., X.X.: Preparing, linking, and unlinking cluster-type polarization-entangled states by integrating modules. Prog. Theor. Exp. Phys. 2013(9), 093A01 (2013)

    Article  Google Scholar 

  70. Wang, X.-W., Zhang, D.-Y., Tang, S.-Q., Xie, L.-J.: Nondestructive Greenberger–Horne–Zeilinger–state analyzer. Quantum Inf. Process. 12(2), 1065–1075 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  71. Dong, L., Xiu, X.-M., Gao, Y.-J., Yi, X.X.: A nearly deterministic scheme for generating \(\chi \)-type entangled states with weak cross-Kerr nonlinearities. Quantum Inf. Process. 12(4), 1787–1795 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  72. Xiu, X.-M., Dong, L., Shen, H.-Z., Gao, Y.-J., Yi, X.X.: Two-party quantum privacy comparison with polarization-entangled Bell states and the Coherent states. Quantum Inf. Comput. 14(3–4), 0236–0254 (2014)

    MathSciNet  Google Scholar 

  73. Shapiro, J.: Single-photon Kerr nonlinearities do not help quantum computation. Phys. Rev. A 73(6), 062305 (2006)

    Article  ADS  Google Scholar 

  74. Shapiro, J.H., Razavi, M.: Continuous-time cross-phase modulation and quantum computation. N. J. Phys. 9(1), 16 (2007)

    Article  Google Scholar 

  75. Gea-Banacloche, J.: Impossibility of large phase shifts via the giant Kerr effect with single-photon wave packets. Phys. Rev. A 81(4), 043823 (2010)

    Article  ADS  Google Scholar 

  76. He, B., Lin, Q., Simon, C.: Cross-Kerr nonlinearity between continuous-mode coherent states and single photons. Phys. Rev. A 83(5), 053826 (2011)

    Article  ADS  Google Scholar 

  77. Feizpour, A., Xing, X., Steinberg, A.M.: Amplifying single photon nonlinearly using weak measurement. Phys. Rev. Lett. 107(13), 133603 (2011)

    Article  ADS  Google Scholar 

  78. Hoi, I.-C., Kockum, A.F., Palomaki, T., Stace, T.M., Fan, B., Tornberg, L., Sathyamoorthy, S.R., Johansson, G., Delsing, P., Wilson, C.M.: Giant cross-Kerr effect for propagating microwaves induced by an artificial atom. Phys. Rev. Lett. 111(5), 053601 (2013)

    Article  ADS  Google Scholar 

Download references

Acknowledgments

This study was supported by the National Natural Science Foundation of China (Grant Nos. 11305016, 61301133, 11271055) and the Research Programs of the Educational Office of Liaoning Province of China (Grant No. L2013425). We acknowledge anonymous reviewers for enlightening instructions.

Author information

Authors and Affiliations

  1. College of Mathematics and Physics, Bohai University, Jinzhou, 121013, People’s Republic of China

    Li Dong, Jun-Xi Wang, Xiao-Ming Xiu & Ya-Jun Gao

  2. School of Physics and Optoelectronic Technology, Dalian University of Technology, Dalian, 116024, People’s Republic of China

    Li Dong, Hong-Zhi Shen, Xiao-Ming Xiu & X. X. Yi

  3. Department of Electrical and Electronics Engineering, Chengdu Technological University, Chengdu, 611730, People’s Republic of China

    Dan Li

Authors
  1. Li Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jun-Xi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hong-Zhi Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiao-Ming Xiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ya-Jun Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. X. X. Yi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiao-Ming Xiu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dong, L., Wang, JX., Shen, HZ. et al. Deterministic transmission of an arbitrary single-photon polarization state through bit-flip error channel. Quantum Inf Process 13, 1413–1424 (2014). https://doi.org/10.1007/s11128-014-0736-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-014-0736-8

Keywords

Search

Navigation