Skip to main content
SpringerLink
Log in

Violation of the “information–disturbance relationship” in finite-time quantum measurements

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

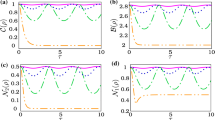
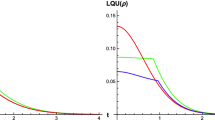
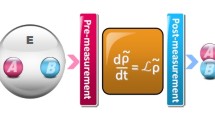
The effect of measurement attributes (quantum level of precision, finite duration) on the classical and quantum correlations is analyzed for a pair of qubits immersed in a common reservoir. We show that the quantum discord is enhanced as the precision of the measuring instrument is increased, and both the classical correlation and the quantum discord experience noticeable changes during finite-time measurements performed on a neighboring partition of the entangled system. The implication of these results on the “information–disturbance relationship” is examined, with critical analysis of the delicate roles played by quantum non-locality and non-Markovian dynamics in the violation of this relationship, which appears surprisingly for a range of measurement attributes. This work highlights that the fundamental limits of quantum mechanical measurements can be altered by exchanges of non-classical correlations such as the quantum discord with external sources, which has relevance to cryptographic technology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. von Neumann, J.: Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton (1955)

    MATH  Google Scholar 

  2. Zeh, H.D.: On the interpretation of measurement in quantum theory. Found. Phys. 1(1), 69–76 (1970)

    Article  ADS  Google Scholar 

  3. Kofman, A.G., Kurizki, G.: Acceleration of quantum decay processes by frequent observations. Nature 405(6786), 546–550 (2000)

    Article  ADS  Google Scholar 

  4. Misra, B., Sudarshan, E.C.G.: The Zeno’s paradox in quantum theory. J. Math. Phys. 18, 756 (1977)

    Article  MathSciNet  ADS  Google Scholar 

  5. Facchi, P., Pascazio, S.: Quantum Zeno dynamics: mathematical and physical aspects. J. Phys. A: Math. Theor. 41, 493001 (2008)

    Article  MathSciNet  Google Scholar 

  6. Facchi, P., Pascazio, S.: Quantum Zeno subspaces. Phys. Rev. Lett. 89, 080401 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  7. Braginsky, V.B., Khalili, F.Ya.: In: Thorne, K.S. (ed.) Quantum Measurement. Cambridge University Press, Cambridge (1992); and references cited therein

  8. Mensky, M.B.: Continuous Quantum Measurements and Path-Integrals. Institute of Physics Publishers, Bristol, Philadelphia (1993)

    Google Scholar 

  9. Zurek, W.H.: Decoherence and the transition from quantum to classical. Phys. Today 44(10), 36 (1991)

    Article  Google Scholar 

  10. Zurek, W.H.: Environment-induced superselection rules. Phys. Rev. D 26, 1862 (1982)

    Article  MathSciNet  ADS  Google Scholar 

  11. Schlosshauer, M.: Decoherence and the Quantum-to-Classical Transition. Springer, Berlin (2008)

    Google Scholar 

  12. Ruskov, R., Korotkov, A.N.: Entanglement of solid-state qubits by measurement. Phys. Rev. B 67, 241305(R) (2003)

    Article  ADS  Google Scholar 

  13. Englert, B.G.: On Quantum Theory. arXiv:quant-ph:arXiv:1308.5290 (2013)

  14. Ollivier, H., Zurek, W.H.: Quantum discord: a measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001)

    Article  ADS  Google Scholar 

  15. Henderson, L., Vedral, V.: Classical, quantum and total correlations. J. Phys. A 34, 6899 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  16. Vedral, V.: Classical correlations and entanglement in quantum measurements. Phys. Rev. Lett. 90, 050401 (2003)

    Article  MathSciNet  ADS  Google Scholar 

  17. Coffman, V., Kundu, J., Wootters, W.K.: Distributed entanglement. Phys. Rev. A 61, 052306 (2000)

    Article  ADS  Google Scholar 

  18. Brodutch, A., Terno, D.R.: Quantum discord, local operations, and Maxwell’s demons. Phys. Rev. A 81, 062103 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  19. Maziero, J., Celeri, L.C., Serra, R.M., Vedral, V.: Classical and quantum correlations under decoherence. Phys. Rev. A 80, 044102 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  20. Mazzola, L., Piilo, J., Maniscalco, S.: Sudden transition between classical and quantum decoherence. Phys. Rev. Lett. 104, 200401 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  21. Ciliberti, L., Rossignoli, R., Canosa, N.: Quantum discord in finite XY chains. Phys. Rev. A 82, 042316 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  22. Datta, A., Shaji, A., Caves, C.M.: Quantum discord and the power of one qubit. Phys. Rev. Lett. 100, 050502 (2008)

    Article  ADS  Google Scholar 

  23. Sacchi, M.F.: Information–disturbance tradeoff in estimating a maximally entangled state. Phys. Rev. Lett. 96, 220502 (2006)

    Article  ADS  Google Scholar 

  24. Maccone, L.: Information–disturbance tradeoff in quantum measurements. Phys. Rev. A 73, 042307 (2006)

    Article  ADS  Google Scholar 

  25. D’Ariano, G.M.: On the Heisenberg principle, namely on the information–disturbance trade-off in a quantum measurement. Fortschritte der Physik 51, 318–330 (2003)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  26. Buscemi, F., Sacchi, M.F.: Information–disturbance trade-off in quantum-state discrimination. Phys. Rev. A 74, 052320 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  27. Maccone, L.: Entropic information–disturbance tradeoff. EPL 77, 40002 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  28. Heisenberg, W.: The Physical Principles of the Quantum Theory. Dover, New York (1930)

  29. Rozema, L.A., Darabi, A., Mahler, D.H., Hayat, A., Soudagar, Y., Steinberg, A.M.: Violation of Heisenberg’s measurement–disturbance relationship by weak measurements. Phys. Rev. Lett. 109, 100404 (2012)

    Article  ADS  Google Scholar 

  30. Wolfgramm, F., Vitelli, C., Beduini, F.A., Godbout, N., Mitchell, M.W.: Entanglement-enhanced probing of a delicate material system. Nat. Photonics 7, 28 (2013)

    Article  ADS  Google Scholar 

  31. Thilagam, A.: Exceptional points and quantum correlations in precise measurements. J. Phys. A 45, 444031 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  32. Feynman, R.P., Hibbs, A.R.: Quantum Mechanics and Path Integrals. McGraw-Hill, New York (1965)

    MATH  Google Scholar 

  33. Feynman, R.P.: Space-time approach to non-relativistic quantum mechanics. Rev. Mod. Phys. 20, 367 (1948)

    Article  MathSciNet  ADS  Google Scholar 

  34. Mensky, M.B.: Quantum restrictions for continuous observation of an oscillator. Phys. Rev. D 20, 384 (1979)

    Google Scholar 

  35. Mensky, M.B.: Quantum restrictions for continuous observation of an oscillator. Sov. Phys. JETP 50, 667 (1979)

    Google Scholar 

  36. Mensky, M.B., Onofrio, R., Presilla, C.: Optimal monitoring of position in nonlinear quantum systems. Phys. Rev. Lett. 70, 2825 (1993)

    Article  ADS  Google Scholar 

  37. Mensky, M.B., Onofrio, R., Presilla, C.: Continuous quantum monitoring of position of nonlinear oscillators. Phys. Lett. A 161, 236–240 (1991)

    Article  ADS  Google Scholar 

  38. Onofrio, R., Presilla, C., Tambini, U.: Quantum Zeno effect with the Feynman–Mensky path-integral approach. Phys. Lett. A 183, 135–140 (1993)

    Article  ADS  Google Scholar 

  39. Tambini, U., Presilla, C., Onofrio, R.: Dynamics of quantum collapse in energy measurements. Phys. Rev. A 51, 967 (1995)

    Article  ADS  Google Scholar 

  40. Audretsch, J., Mensky, M.: Continuous fuzzy measurement of energy for a two-level system. Phys. Rev. A 56, 44 (1997)

    Article  ADS  Google Scholar 

  41. Heiss, W.D.: Repulsion of resonance states and exceptional points. Phys. Rev. E 61, 929 (2000)

    Article  ADS  Google Scholar 

  42. Salles, A., de Melo, F., Almeida, M.P., Hor-Meyll, M., Walborn, S.P., Ribeiro, P.S., Davidovich, L.: Experimental investigation of the dynamics of entanglement: sudden death, complementarity, and continuous monitoring of the environment. Phys. Rev. A 78, 022322 (2008)

    Article  ADS  Google Scholar 

  43. Sudarshan, E.C.G., Mathews, P.M., Rau, J.: Stochastic dynamics of quantum-mechanical systems. Phys. Rev. 121, 920–924 (1961)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  44. Kraus, K.: States, Effects, and Operations: Fundamental Notions of Quantum Theory. Springer, Berlin (1983)

    Book  MATH  Google Scholar 

  45. Bell, J.S.: On the Einstein–Podolsky–Rosen paradox. Physics 1, 195–200 (1964)

    Google Scholar 

  46. Clauser, J.F., Horne, M.A., Shimony, A., Holt, R.A.: Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969)

    Article  ADS  Google Scholar 

  47. Bellomo, B., Franco, R.L., Compagno, G.: Dynamics of non-classically-reproducible entanglement. Phys. Rev. A 78, 062309 (2008)

    Article  ADS  Google Scholar 

  48. Galve, F., Giorgi, G.L., Zambrini, R.: Orthogonal measurements are almost sufficient for quantum discord of two qubits. Europhys. Lett. (EPL) 96, 40005 (2011)

    Article  ADS  Google Scholar 

  49. Szilard, L.: Uber die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Zeitschrift fr Physik 53(11–12), 840–856 (1929)

    Article  ADS  MATH  Google Scholar 

  50. Jozsa, R.: Fidelity for mixed quantum states. J. Mod. Opt. 41(12), 2315–2323 (1994)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  51. Anandan, J., Aharonov, Y.: Geometry of quantum evolution. Phys. Rev. Lett. 65, 1697 (1990)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  52. Wolf, M.M., Eisert, J., Cubitt, T.S., Cirac, J.I.: Assessing non-Markovian quantum dynamics. Phys. Rev. Lett. 101, 150402 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  53. Rajagopal, A.K., Devi, A.U., Rendell, R.W.: Kraus representation of quantum evolution and fidelity as manifestations of Markovian and non-Markovian forms. Phys. Rev. A 82, 042107 (2010)

    Article  ADS  Google Scholar 

  54. Breuer, H.P., Laine, E.M., Piilo, J.: Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 103, 210401 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  55. Hall, M.A., Altepeter, J.B., Kumar, P.: Drop-in compatible entanglement for optical-fiber networks. Opt. Express 17, 14558–14566 (2009)

    Article  ADS  Google Scholar 

  56. Tittel, W., Brendel, J., Zbinden, H., Gisin, N.: Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81, 3563 (1998)

    Article  ADS  Google Scholar 

  57. Caruso, F., Chin, A.W., Datta, A., Huelga, S.F., Plenio, M.B.: Highly efficient energy excitation transfer in light-harvesting complexes: the fundamental role of noise-assisted transport. J. Chem. Phys. 131, 105106–105106 (2009)

    Article  ADS  Google Scholar 

  58. Rebentrost, P., Mohseni, M., Aspuru-Guzik, A.: Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. B 113, 9942–9947 (2009)

    Article  Google Scholar 

  59. Thilagam, A.: Non-Hermitian exciton dynamics in a photosynthetic unit system. J. Chem. Phys. 136, 065104 (2012)

    Article  ADS  Google Scholar 

  60. Thilagam, A.: Multipartite entanglement in the Fenna–Matthews–Olson (FMO) pigment–protein complex. J. Chem. Phys. 136, 175104 (2012)

    Article  ADS  Google Scholar 

  61. Thilagam, A., Usha Devi, A.R.: Non-Markovianity and Clauser–Horne–Shimony–Holt (CHSH)-Bell inequality violation in quantum dissipative systems. J. Chem. Phys. 137, 215103–215103 (2012)

    Article  ADS  Google Scholar 

  62. Caram, J.R., Lewis, N.H., Fidler, A.F., Engel, G.S.: Signatures of correlated excitonic dynamics in two-dimensional spectroscopy of the Fenna–Matthew–Olson photosynthetic complex. J. Chem. Phys. 137, 024507 (2012)

    Article  ADS  Google Scholar 

Download references

Acknowledgments

This research was undertaken on the NCI National Facility in Canberra, Australia, which is supported by the Australian Commonwealth Government. The author gratefully acknowledges the support of the Julian Schwinger Foundation Grant, JSF-12-06-0000. The author would like to thank the anonymous referees for helpful comments.

Author information

Authors and Affiliations

  1. Information Technology, Engineering and Environment, Mawson Institute, University of South Australia, Adelaide, 5095, Australia

    A. Thilagam

Authors
  1. A. Thilagam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Thilagam.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Thilagam, A. Violation of the “information–disturbance relationship” in finite-time quantum measurements. Quantum Inf Process 13, 151–169 (2014). https://doi.org/10.1007/s11128-013-0673-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-013-0673-y

Keywords

Search

Navigation