Skip to main content
SpringerLink
Log in

Distort one qubit from copying and deleting

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

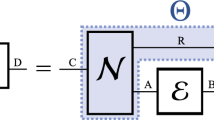
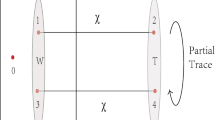
Immeasurability of a quantum state has important consequence in practical implementation of quantum computers. Our purpose is to analyze the efficiency of the entangled output of Pati-Braunstein deleting machine or Wootters-Zurek quantum copying machine as a quantum channel. Interestingly we find that for special values of the input parameter the state does not violate the Bell’s inequality. Moreover, we analyze the performances of the entangled output of Pati-Braunstein deleting after the Wootters-Zurek copying machine.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wootters W.K., Zurek W.H.: A single quantum cannot be cloned. Nature 299, 802 (1982)

    Article  ADS  Google Scholar 

  2. Yuen H.P.: Amplification of quantum states and noiseless photon amplifiers. Phys. Lett. A 113, 405 (1986)

    Article  MathSciNet  ADS  Google Scholar 

  3. Duan L.M., Guo G.C.: A probabilistic cloning machine for replicating two non-orthogonal states. Phys. Lett. A 243, 261 (1998)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  4. Duan L.M., Guo G.C.: Probabilistic cloning and identification of linearly independent quantum states. Phys. Rev. Lett. 80, 4999 (1998)

    Article  ADS  Google Scholar 

  5. Pati A.K.: Quantum superposition of multiple clones and the novel cloning machine. Phys. Rev. Lett. 83, 2849 (1999)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  6. Cerf N.: Asymmetric quantum cloning machines in any dimension. J. Mod. Opt. 47, 187 (2000)

    MathSciNet  ADS  Google Scholar 

  7. Gisin N., Massar S.: Optimal quantum cloning machines. Phys. Rev. Lett. 79, 2153 (1997)

    Article  ADS  Google Scholar 

  8. Bruß D., Ekert A., Macchavello C.: Optimal universal quantum cloning and state estimation. Phys. Rev. Lett. 81, 2598 (1998)

    Article  ADS  Google Scholar 

  9. Bužek V., Hillery M.H.: Universal optimal cloning of arbitrary quantum states: from qubits to quantum registers. Phys. Rev. Lett. 81, 5003 (1998)

    Article  ADS  Google Scholar 

  10. Fan H., Imai H., Matsumoto K., Wang X.-B.: Phase-covariant quantum cloning of qudits. Phys. Rev. A 67, 022317 (2003)

    Article  ADS  Google Scholar 

  11. Sacchi M.F.: Phase-covariant cloning of coherent states. Phys. Rev. A 75, 042328 (2007)

    Article  ADS  Google Scholar 

  12. Kay A., Kaszlikowski D., Ramanathan R.: Optimal cloning and singlet monogamy. Phys. Rev. Lett. 103, 050501 (2009)

    Article  ADS  Google Scholar 

  13. Bartkiewicz K., Miranowicz A., Özdemir S.K.: Optimal mirror phase-covariant cloning. Phys. Rev. A 80, 032306 (2009)

    Article  ADS  Google Scholar 

  14. Massar S., Popescu S.: Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259 (1995)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  15. Derka R., Bužek V., Ekert A.: Universal algorithm for optimal estimation of quantum states from finite ensembles via realizable generalized measurement. Phys. Rev. Lett. 80, 1571 (1998)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  16. Dobšíček M., Johansson G., Shumeiko V., Wendin G.: Arbitrary accuracy iterative quantum phase estimation algorithm using a single ancillary qubit: a two-qubit benchmark. Phys. Rev. A 76, 030306(R) (2007)

    ADS  Google Scholar 

  17. García-Mata I., Shepelyansky D.L.: Quantum phase estimation algorithm in presence of static imperfections. Eur. Phys. J. D 47, 151–156 (2008)

    Article  ADS  Google Scholar 

  18. Bennett C.H., Brassard G., Crépeau C., Jozsa R., Peres A., Wootters W.K.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  19. Szilard L.: Uber die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z.Phys 53, 840 (1929)

    Article  ADS  MATH  Google Scholar 

  20. Landauer R.: Irreversibility and heat generation in the computing proce. IBM J. Res. Dev. 3, 183 (1961)

    Article  MathSciNet  Google Scholar 

  21. Zurek W.H.: Quantum cloning: Schrödinger’s sheep. Nature 404, 131 (2000)

    Article  Google Scholar 

  22. Pati A.K., Braunstein S.L.: Impossibility of deleting an unknown quantum state. Nature 404, 164 (2000)

    Article  ADS  Google Scholar 

  23. Pati A.K., Braunstein S.L.: Quantum no-deleting principle and some of its implications. arXiv:quant-ph/0007121v1

  24. Bužek V., Hillery M.H.: Quantum copying: beyond the no-cloning theorem. Phys. Rev. A 54, 1844–1852 (1996)

    Article  MathSciNet  ADS  Google Scholar 

  25. Peres A.: Separability criterion for density matrices. Phys. Rev. Lett. 77, 1413 (1996)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  26. Horodecki M., Horodecki P., Horodecki R.: Separability of mixed states: necessary and sufficient conditions. Phys. Lett. A 223, 1 (1996)

    Article  MathSciNet  ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Information Security Center, School of Information Science and Technology, Southwest Jiaotong University, Chengdu, 610031, China

    Ming-Xing Luo

  2. Institute of Computer Science, Sichuan University of Science Engineering, Zigong, 64300, China

    Yun Deng

Authors
  1. Ming-Xing Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yun Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ming-Xing Luo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, MX., Deng, Y. Distort one qubit from copying and deleting. Quantum Inf Process 12, 1701–1717 (2013). https://doi.org/10.1007/s11128-012-0484-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-012-0484-6

Keywords

Search

Navigation