Abstract
In an influential paper, Färe and Lovell (J Econ Theory 19:150–162, 1978) proposed an (input based) technical efficiency index designed to correct two fundamental inadequacies of the Debreu-Farrell index: its failure to satisfy (1) indication (the index is equal to 1 if and only if the input bundle is technically efficient) and (2) weak monotonicity (an increase in any one input quantity cannot increase the value of the index). Färe et al. (1985) extended the index to measure efficiency in the full space of input and output quantities. Unfortunately, this index fails to satisfy not only indication and monotonicity at the boundary (of output space), but also weak monotonicity. We show, however, that a simple modification of the index corrects these flaws. To demonstrate the tractability of our proposal, we apply it to baseball batting performance, in which zero outputs occur frequently.





Similar content being viewed by others
Notes
See Russell (1985).
Our modification is not needed to maintain indication and weak monotonicity of the input-based FL index at the boundary of input space.
All but free disposability of these conditions are necessary to guarantee that our efficiency indexes are well defined. Free disposability could be dispensed with (theoretically); the only change that would be needed in what follows would be to redefine the inefficiency indexes on the free-disposal hull of \(T, T+({\bf R}^n_{+} \times -{\bf R}^m_+),\) rather than on T itself (as in Russell 1987 for input-based efficiency indexes).
Vector notation: \(\bar{x}\ge x\) if \(\bar{x}_i\ge x_i\) for all \(i;\,\bar{x}> x\) if \(\bar{x}_i\ge x_i\) for all i and \(\bar{x}\ne x\); and \(\bar{x}\gg x\) if \(\bar{x}_i> x_i\) for all i.
FGL order coordinates so that the first k input quantities and first l output quantities are positive and then minimize only over the sum of these k + l coordinates, all of which have positive values. Our characterization does not require a permutation of the coordinates whenever a production vector (or a technology) is changed.
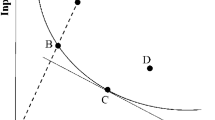
For the sake of symmetry, we weight each input-contraction factor by \(\delta(x_i),\,i=1,\ldots n\), but the index would be unaffected by omitting these weights, since the value of α i at the minimum is zero if x i = 0. In the initial specification of the FGL index (p. 154), α is restricted to be strictly positive, in which case their minimization problem has no solution if, for some i, x i > 0 and the minimum value of α i is zero; this case is illustrated in Fig. 2, where \(x^{\prime}\) would be contracted to \(\hat{x}\). In their characterization of the domain of the index (p. 153), however, they restrict α to be non-negative. We choose the latter formulation to ensure that the index is well-defined on the domain, which includes input and output quantities with zero values.
Note that we are able to use the min operator instead of inf even though the constraint set \(\Upomega(x,y,T)\) is not closed because, using inf, \({\mathop{\beta}\limits^{\ast}}_{j}=0\) only if δ(y j ) = 0, in which case β j does not appear in the objective function in (2.2).
Neither of the indexes we consider satisfies the stronger property of (strict) monotonicity. Nor does either satisfy continuity. See Russell and Schworm (2011) for details.
And replacing min with inf.
Note that we must use the infimum here, because ψ j (x, y, T) can be non-zero when y j = 0.
And, of course, in this formulation \({\mathop{\alpha}\limits^{\ast}}_i\) is an arbitrary selection from [0, 1] if δ(x i ) = 0. Note that, in addition to this arbitrariness, the “solution” values for α i or β j not associated with zero values of x i or y j need not be unique, since there can be ties in the optimization problem.
In fact, it will be lower, since the zeros in the optimal values of the numerator and denominator will be replaced by a zero in the numerator and a 1 in the denominator.
As noted above, the minimum is well defined (no attempt to divide by zero): since \(y_j^{d^{\prime}}\) is non-zero and the output constraint set is bounded, the solution value for each β j will be non-zero.
The programming codes are available at http://www.economics.ucr.edu/people/russell/index.html.
References
Anderson T, Sharp GP (1997) A new measure of baseball batters using DEA. Ann Oper Res 73:141–155
Briec W (1997) A graph type extension of Farrell technical efficiency. J Prod Anal 8:95–110
Charnes A, Clark CT, Cooper WW, Golany B (1984) A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the US air force. Ann Oper Res 2:95–112
Chung Y, Färe R, Grosskopf S (1997) Productivity and undesirable outputs: a directional distance function approach. J Environ Manag 51:229–240
Cooper WW, Seiford LM, Tone K, Zhu J (2007) Some models and measures for evaluating performances with DEA: past accomplishments and future prospects. J Prod Anal 28:151–164
Färe R, Grosskopf S (2000) Theory and application of directional distance functions. J Prod Anal 13:93–103
Färe R, Lovell CAK (1978) Measuring the technical efficiency of production. J Econ Theory 19:150–162
Färe R, Grosskopf S, Lovell CAK (1985) The measurement of efficiency of production. Kluwer-Nijhoff, Boston
Färe R, Grosskopf S, Lovell CAK (1994) Production frontiers. Cambridge University Press, Cambridge
Farrell MJ (1956) The measurement of productive efficiency. J R Stat Soc Ser A Gen 120:253–282
Koopmans TC (1951) Analysis of production as an efficient combination of activities. In: Koopmans TC (ed) Activity analysis of production and allocation. Physica-Verlag, Heidelberg
Luenberger DG (1992) New optimality principles for economic efficiency and equilibrium. J Optim Appl 75:221–264
Mazur MJ (1995) Evaluating the relative efficiency of baseball players. In: Charnes A, Cooper WW, Lewin AY, Seiford LM (eds) Data envelopment analysis: theory, methodology and applications. Kluwer, Boston
Russell RR (1985) Measures of technical efficiency. J Econ Theory 35:109–126
Russell RR (1987) On the axiomatic approach to the measurement of technical efficiency. In: Eichhorn W (ed) Measurement in economics: theory and application of economic indices. Physica-Verlag, Heidelberg
Russell RR, Schworm W (2011) Properties of inefficiency indexes on \(\langle \hbox{input}, \hbox{output}\rangle\) space. J Prod Anal (forthcoming)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Levkoff, S.B., Russell, R.R. & Schworm, W. Boundary problems with the “Russell” graph measure of technical efficiency: a refinement. J Prod Anal 37, 239–248 (2012). https://doi.org/10.1007/s11123-011-0241-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-011-0241-3