Abstract
We introduce the conflict interaction with two positions between a couple of image probability measures and consider the associated dynamical system. We prove the existence of invariant limiting measures and find the criteria for these measures to be a pure point, absolutely continuous, or singular cotinuous as well as to have any topological type and arbitary Hausdorff dimension.
Similar content being viewed by others
References
S. Albeverio, V. Koshmanenko, G. Torbin, Fine structure of the singular continuous sperctrum, Meth. Funct. Anal. Topol. 9(2) (2003), 101–127.
S. Albeverio, V. Koshmanenko, M. Pratsiovytyi, and G. Tprbin,
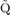 -representation of real numbers and fractal probability distribution, subm. to Infinite Dimensiional Analysis, Quantum Probability and Related Topics.
-representation of real numbers and fractal probability distribution, subm. to Infinite Dimensiional Analysis, Quantum Probability and Related Topics.M. F. Barnsley, and S. Demko, Iterated functional system and the global constuction of fractals, Proc. Roy. Soc. London A, 399 (1985), 243–275.
S. D. Chatterji, Certain induced measures on the unit interval, J. London Math. Soc.,38(1962),325–331.
S. Kakutani, Equivalence of infinite product measures, Ann. Math., 49 (1948), 214–224.
V. Koshmanenko, The theorem of conflicts for a pair of stochastic vectors, Ukrainian Math. J., 55(4) (2003), 555–560.
V. Koshmanenko, The theorem of conflicts for a couple of probability measures, accepted to publ. in Math. Meth. Oper. Res., 59(2) (2004).
M. V. Pratsiovytyi, Fractal, superfractal and anomalously fractal distribution of random variables with a fixed infinite set of independent n-adic digits, Exploring Stochastic Laws VSP (1995), 409–416.
M. V. Pratsiovytyi, Fractal approach to investigation of singular distributions (in Ukrainian) National Pedagogical Univ., Kyiv, 1998.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Albeverio, S., Koshmanenko, V., Pratsiovytyi, M. et al. Spectral Properties of Image Measures Under the Infinite Conflict Interaction. Positivity 10, 39–49 (2006). https://doi.org/10.1007/s11117-005-0012-3
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11117-005-0012-3




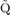 -representation of real numbers and fractal probability distribution, subm. to Infinite Dimensiional Analysis, Quantum Probability and Related Topics.
-representation of real numbers and fractal probability distribution, subm. to Infinite Dimensiional Analysis, Quantum Probability and Related Topics.