This study examines the association between two measures of teaching effectiveness—a student survey measure and a classroom observation measure—to determine whether the correlation depends on the study design. Educational policies around the globe show increasing interest in measuring high-quality, highly effective teaching (e.g., Isoré 2009; Mourshed et al. 2010; National Council on Teacher Quality [NCTQ], 2013). Currently, most of these policies maintain that valid identification of high-quality teaching requires multiple measures that together reflect the complexity of the construct (Darling-Hammond 2013; Goe and Croft 2009; Martínez et al. 2016; Marzano and Toth 2013). But, although using multiple measures increases face validity, it also raises questions about appropriate ways to combine measures to inform a single decision.

In their study of the accuracy of decisions based on multiple measures, including classroom observations and student surveys, Martínez et al. (2016) examine various decision models to combine measures to inform a single decision. Some of their models specify decision rules to apply to separate measures whereas other models synthesize measures into a single composite. Although their study is comprehensive, with important insights, its conclusions are weakened by limitations of their approach, in specific “In this type of application, we lack a substantive or empirical basis for determining which model yields the true or correct classifications and inferences. There is thus no true performance classification we can judge all models against” (Martínez et al. 2016, p. 751, emphasis in original). Empirical determinations of a true or correct classification typically rely on reducing measurement error (thus improving reliability of the composite), such that the person’s true (composite) score shows only minor deviations from the person’s scores on the separate measures. This study applies generalizability theory. Generalizability theory can be used to examine how adaptation of study designs reduce measurement error and improve reliability. This is of interest to researchers and policy makers seeking empirical evidence how to construct more reliable composite scores. Less known is that the generalizability coefficient can equal the Pearson correlation coefficient (Kane and Brennan 1977; Fan and Sun 2014; Traub 1994). Hence, an alternative use of generalizability theory is to examine whether the association between measures depends on the study design. This is of interest to researchers and policy makers seeking how to enhance complementarity of multiple measures. Therefore, the current study also applies generalizability theory to explore whether the correlation between a classroom observation and a student survey measure of teaching effectiveness varies with different study designs.

This study represents, to some extent, a continuation of Spearman’s (1904) article “The Proof and Measurement of Association between Two Things,” which work highlights concerns for attenuation of correlation, i.e., spuriously low (or high) correlations between measures, caused by (un)systematic errors inherent in the study design. Here again, generalizability theory provides a mean to explore whether correlation size might be attenuated by systematic errors. In this sense, generalizability theory might contribute to an expanded understanding of the variations in correlation size that appear in previous studies that examine the correlation between observation and survey measures (e.g., Maulana and Helms-Lorenz 2016; Murray 1983).

1 Background

The study explores the association between two measures of teaching effectiveness. For this study, teaching effectiveness is a latent variable, operationalized by items that describe observable teaching practices known to contribute to student learning (Muijs et al. 2014). The concept of teaching effectiveness focuses on teachers’ teaching practices and is believed to be distinct from the concept of teaching quality, which instead is operationalized using student achievement test scores.

The study focus is on situations in which researchers or schools apply both classroom observation and student survey measures, which differ in their exact item content but are believed to operationalize the same latent construct. For example, studies attempting to validate interpretations of scores on existing instruments sometimes apply two instruments assumed to measure the same latent construct but which differ in their exact item content (e.g., Howard et al. 1985; Maulana and Helms-Lorenz 2016). Also, various state agencies or the schools themselves apply multiple measures of effectiveness that differ in terms of exact item content and use the information gathered through both measures to inform their personnel decisions (e.g., Ferguson and Danielson 2015; Martínez et al. 2016). In studying this situation, this research explicitly confounds the content of the instrument items with the type of rater (i.e., observer or student), in an effort to explore whether the association between classroom observation and student survey measures is attenuated by (un)systematic errors inherent in the study design. The study does not, and cannot, address alternative explanations that possibly lower correlations such as differences in maturity of students and observers or differences in exact item content.

1.1 The association between survey and observation measures

Few studies have documented the correlations between observation and survey measures. Most that do report modest correlations in the range of 0.15 to 0.30 (e.g., De Jong and Westerhof 2001; Ferguson and Danielson 2015; Howard et al. 1985; Martínez et al. 2016; Maulana and Helms-Lorenz 2016). These studies provide various interpretations of these correlations. With respect to validity, some studies interpret modest positive correlations as supportive of measurement validity (De Jong and Westerhof 2001; Maulana and Helms-Lorenz 2016) and argue that their findings confirm the general expectation that measures are positively associated. Others (Howard et al. 1985; Martínez et al. 2016) note differences in correlation size when comparing same-method measures (e.g., alumni survey and student survey) with other-method measures (e.g., survey and classroom observation) and argue that the modest correlations appear low, relative to the same-method correlations. The different interpretations also seem loosely related to different viewpoints about the anticipated use of the measures. De Jong and Westerhof (2001) and Maulana and Helms-Lorenz (2016) interpret the relevance of these correlations for a low-stakes scientific usage situation; Martínez et al. (2016) and Howard et al. (1985) interpret them in the context of evaluative usage.

An exception to these reports of modest correlations comes from Murray (1983), who reports a correlation of 0.76, possibly because this author implemented a more comprehensive design in which multiple (six–eight) observers visited multiple (three) lessons of the class. He also correlated these data with student ratings obtained in the same class. The use of multiple observers visiting multiple lessons increases the reliability of classroom observation measures (e.g., Charalambous et al. 2017; Hill et al. 2012; Kane et al. 2012; Praetorius et al. 2014). Moreover, unreliability in measurements also attenuates the correlation between measures (Spearman 1904). This evidence provides support for the speculation that the association between survey and observation measures increases if the standard classroom observation design is adapted, such that multiple lessons are visited by multiple observers. However, not all evidence supports this speculation. Martínez et al. (2016) also use observation scores of multiple (four) lessons by different (two) observers and report relatively modest correlations (ranging from 0.15 to 0.30). The striking difference between these results and those reported by Murray (1983) might to some signal that the correlation is not attenuated by measurement error but instead depends on the instrument content: Martínez et al. (2016) use observer scores obtained with 8 items, all related to instruction, whereas Murray had observers score 60 items, divided across eight categories of classroom behavior (speech, nonverbal behavior, explanation, organization, interest, task orientation, rapport, and participation). Others might attribute the difference as signaling the correlation depends on the scoring quality provided by students of different age, such as between those in elementary education in the Martinez et al. (Martínez et al. 2016) dataset versus the higher-education students in Murray’s (1983) data set. However, technical differences between the studies complicate direct comparisons. Martínez et al.’s (2016) study is embedded in the Measures of Effective Teaching (MET) project, in which teachers’ scores are estimated by a regression equation that controls the observation and survey scores for several covariates, including students’ prior-year test score (see also Mihaly et al. 2013). The residuals of this equation then are interpreted as unbiased survey and observation scale scores. This approach deviates from typical practice, such as Murray’s (1983) method, which uses the average or sum of all item responses to estimate teachers’ scores, and this difference possibly influences the correlation between measures.

In summary, the mixed results restrict conclusions about whether correlations are attenuated by measurement error. Even perfectly reliable measures might have small correlations. Therefore, this study sets out to evaluate empirically whether the association between classroom observations and student survey measures depends on the number of classroom observers, as well as some other features of standard survey and classroom observation designs.

1.2 Differences between standard classroom observation and survey designs

Some differences between standard survey and classroom observation designs are well established (e.g., Benton and Cashin 2012; Muijs 2006; van der Lans et al. 2015). One notable difference pertains to stability in scores of the same teacher across different lessons (Benton and Cashin 2012; Muijs 2006). A standard student survey item does not refer to any specific lesson (e.g., “This teacher uses clear examples”), so students likely summarize their experiences across multiple lessons. Evidence supports such a lesson-generic interpretation: Costin (1968) reports no difference in higher-education students’ average ratings administered at the middle versus the end of the semester. (Carrier et al. 1974) similarly find no differences in students’ average ratings, 1 week prior or 1 day prior to an exam. According to Mainhard et al. (2011), secondary education students’ ratings of controlling and affiliative teacher behaviors remain stable during the first 14 weeks of the school year. Beyond education research, social psychologists address stability in people’s perceptions of others. Kenny (2004) estimates a lower bound correlation of 0.71 between ratings by the same rater of another person on two subsequent occasions. These findings should not be taken as an argument that student surveys must be lesson-generic; rather, this evidence pertains to studies that use a generic survey question format. Survey items such as, “In this lesson, the teacher used clear examples,” might prompt less stable ratings. In contrast with such general stability though, scores on classroom observation measures vary more across different lessons (Muijs 2006; Praetorius et al. 2014). Classroom observers have no knowledge of previous lessons, so even if the question format is lesson-generic, they have no other experiences to consider. Muijs (2006) therefore refers to classroom observation measures as “snapshots” of information about teachers’ generic teaching effectiveness.

Another difference between survey and classroom observation measures reflects the method they use to handle observer effects, which refer to the influence of an observer’s personal norms and beliefs about what good teaching entails. Classroom observation designs usually rely on observation training to minimize disagreement between observers (Muijs 2006). Typically, only a few observers are trained and each trained observer must visit many teachers. With this design, the observer’s perceptions potentially biases the scores earned by many teachers; the cumulative impact of even small observer effects on correlations with other variables may be considerable. In contrast, student survey designs rely on class average scores provided by many (untrained) students (Marsh 2007). Typically, each student scores one or a few teachers. Therefore, the observer effect associated with each student biases the scores of fewer teachers, and the cumulative impact of even substantial student observer effects on correlations with other variables may be minimal (Marsh 2007).

Finally, correlations between observation and survey measures might be attenuated because standard observation and survey designs match each teacher with one class, thereby prohibiting the separation of teacher and class effects. At least one study indicates that scores on student survey measures may depend on class composition (e.g., Levy, Wubbels, den Brok, & Brekelmans, Levy et al. 2003). With respect to classroom observation measures, two studies indicate that scores may depend on class composition (Kane et al. 2012; Lei, Li, & Leroux, Lei et al. 2018). In contrast with observer effects, there is no agreed-on substantive interpretation of class effects in survey and classroom observation research. Lei et al. (2018) discuss several proposed explanations including the interpretation that some classes may be more challenging to teach. This study follows this interpretation and will view class effects as reflecting variation in teachability of classes. Teachers assigned to more teachable classes earn higher evaluation scores, because their class is easier to teach (e.g., most students are intrinsically interested in the topic or able to understand complicated instructions). Correlations between observation and survey measures then might be attenuated by these class effects. If class effects correlate positively and the design confounds teacher and class effects, this positive correlation might get added to the correlation due to teacher effects, leading to spuriously high correlations between the two measures (i.e., higher than expected for designs that more appropriately separate class and teacher effects). Alternatively, if class effects correlate negatively, the negative correlation would get subtracted from the correlation between teacher effects, and the application of standard designs would lead to spuriously low correlations (i.e., lower than expected for designs that adequately separate teacher and class effects). This discussion accordingly leads to a central research question:

To what extent does the association between student survey and classroom observation measures depend on the study design?

2 Hypotheses

In line with Murray (1983) and ample evidence that classroom observation reliability increases substantially when an increasing number of observers visit different lessons (e.g., Charalambous et al. 2017; Hill et al. 2012; Praetorius et al. 2014; van der Lans et al. 2016), this study predicts that the association between student survey and classroom observation measures increases with the number of lesson visits by different observers. Formally,

  • H10: The association between the survey and classroom observation measures decreases or does not increase with an increasing number of classroom observations.

  • H11: The association between the survey and classroom observation measures increases with an increasing number of classroom observations.

To examine the impact of study designs on the association between observation and survey measures further, this study also compares a completely nested design with partially nested design. The latter design allows for the separation of teacher and class effects and provides thus a cleaner estimation of the correlation between classroom observation and student survey measures. Therefore,

  • H20: The association between the survey and classroom observation measures does not change if the survey and observation design shift from nested to partially nested.

  • H21: The association between the survey and classroom observation measures changes if the survey and observation design shift from nested to partially nested.

3 Method

This research was embedded in a larger research project exploring how schools can organize and implement evaluations of in-service teachers using collegial visitation and student survey ratings. The project met university standards for the principles and ethics of human subject research. Participation in the project was voluntary, and participating schools received no funding.

3.1 Design and data gathering procedure

The study took place in the Dutch secondary education system, which students enter at approximately 12 years of age. The system assigns students into six tracks (pre-university education, higher vocational preparatory education, and four tracks of middle and lower vocational preparatory education; OECD 2016). In all tracks, education comprises two main phases: basic (“onderbouw”) and specialized (“bovenbouw”), organized differently. This study investigates students and lessons in basic education, which spans 2 years for students in middle and lower vocational preparatory education and 3 years for students in higher vocational preparatory and pre-university education. Students are grouped into classes and follow all standard courses with the same peers; only at the end of each school year may students be assigned to another class.

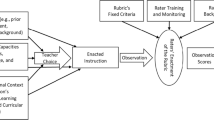
The data gathering procedure was constructed around classes of students (Fig. 1). Within a selected class, we sampled four teachers. Sampling was nonrandom and aimed at mathematics, Dutch, English (as a foreign language), and history teachers. Teachers could not participate in multiple classes. If multiple classes in one school participated, each new class was connected to four new teachers. All participating teachers observed lessons given by colleagues teaching the same class. Because four teachers were sampled per class, every teacher should have received three lesson visits (see Fig. 1).

Fig. 1
figure 1

Visualization of the data gathered for one specific class sampled within a school

Full size image

The procedure was complex for schools to implement, and some schools adjusted it. Most frequently, schools encountered problems in scheduling lesson visits between two or more colleagues (e.g., teacher A teaches history to a particular class on Monday and Thursday, but teacher C is not working on those days). Sometimes another colleague could step in, but in other instances, the planned observation did not take place. Of the 56 teachers, 8 (14%) received no third classroom observation. In addition, some schools could not sample four teachers, and on some few occasions a teacher dropped out. Therefore, we accepted groups of three teachers per class. In total, 11 classes counted four teachers and 4 classes counted three teachers. If groups counted three teachers, the third observation was performed by a colleague from “outside” (i.e., not teaching that particular class) who was trained in observing lessons. In one specific instance, the school had all observations performed by formal coaches working inside the school instead of colleagues. Although these coaches had much more experience with observation than typical teachers, analyses revealed no relevant differences between these experienced coaches and colleagues’ observations in terms of their means and variances (see supplementary file). Thus, we included these data.

3.2 Sample

The study combined classroom observation and student survey scores of the same 56 teachers. These teachers taught 15 different classes in eight different secondary education schools, mostly located in the center and south of the Netherlands. Different peer-colleagues visited and observed lessons of these 56 teachers. In total, the sample counted 46 unique peer-observers working at these same eight schools. All but one peer-observer participated in observation training prior to their first lesson visit. All peer-observers had prior teaching experience ranging from 1 to 40 years, and 67.5% of them were men. This unequal gender distribution calls for further examination of potential bias, but the analyses revealed no relevant differences (see supplementary file).

For these same 56 teachers, 1305 student surveys were available, rated by 366 students. Student ages varied between 12 and 17 years, though more than 90% were between 13 and 15 years of age, and 52.3% were girls.

3.3 Instruments

“My teacher” student survey

The “My Teacher” student survey consists of 40 items related to students’ perceptions of teachers’ teaching practice (e.g., “My teacher applies clear rules,” “My teacher stimulates my thinking,” “My teacher ensures that I use my time effectively”). The items are scored on a dichotomous scale coded 0 = “rarely” and 1 = “often.” They can be grouped in six domains: safe learning climate (SLC), efficient classroom management (ECM), clarity of instruction (COI), activating teaching methods (ATM), teaching learning strategies (TLS), and differentiation in instruction (DII) (for an extensive review of these six domains, see Van de Grift 2014). Although the survey can be subdivided, doing so merely facilitates interpretation. Evidence suggests that the survey measures a single latent distribution (Maulana et al. 2015; van der Lans et al. 2015). The estimates of internal consistency rely on formulas described by (Raju et al. 2006) and is ρ(xx′) = .88. The interpretation of Raju et al.’s (2006) coefficient is similar to the more commonly reported Cronbach’s alpha, but this measure is more appropriate for dichotomous Rasch-scaled item responses.

ICALT observation instrument

The ICALT classroom observation instrument consists of 32 items reflecting observable teaching practices (e.g., “Uses teaching methods that activate students”). Items can be grouped in the SLC, ECM, COI, ATM, TLS, and DII domains from the “My Teacher” survey. Observers score the items using a four-point scale: 1 = “not performed,” 2 = “insufficiently performed,” 3 = “sufficiently performed,” and 4 = “well performed.” To make comparisons, the scores were dichotomized, such that the original scores 1 and 2 were recoded to 0, and the original codes 3 and 4 were recoded to 1. The outcomes offered no evidence that the dichotomization led to any unacceptable loss of information (see supplementary file).

Like the student survey, the lesson observation form can be subdivided into six domains, but evidence suggests that the observation form measures a single latent distribution (van de Grift et al. 2014; van der Lans et al. 2018). The internal consistency of this latent distribution (Raju et al. 2006) is ρ(xx′) = 78.

3.4 Data selection

After checking the data for outliers and missing values, eight classroom observation forms with too many missing values (> 8) were excluded. Three of these eight removed forms related to the same teacher, so this teacher also was removed from the analysis. Of the student data, 43 surveys counted more than five missing values and were discarded. In addition, 51 surveys had no valid identification. Because the survey design required a means to identify surveys completed by the same student, these entries were removed as well. Students who had responded on only one or two surveys were removed too (n = 62), because they would contribute unequally to the different variance components studied.

The eligible data contained 1121 surveys by 305 students. The surveys were unequally distributed over the classes and teachers: Some teachers had only 10 valid surveys, whereas others had 30. This considerable imbalance was cause for concern, because imbalanced groupings could lead to biased variance estimations and convergence problems. Therefore, it was decided to sample nine students randomly from each class; in total, 485 surveys by 134 students entered the analysis, to be correlated with 160 observation forms by 46 peer-observers.

The considerable number of excluded surveys calls for an examination whether the selected 485 surveys are representative of the unselected 636 surveys. A second sample of 485 surveys by 134 students thus was obtained; some classes counted fewer than 18 students, so it was impossible to select two completely different groups of nine students. The validation sample included 430 new surveys from 116 students, which represent the majority of the 636 unselected surveys. Apart from some minor discrepancies, the results for the second validation sample overlap with the here reported results (see the supplementary file). The discrepancies suggest that the subsample of selected students shows a slightly larger observer effect and a slightly larger teacher × observer interaction effect. This suggests that the correlation might have been by 0.03 points higher.

3.5 Analysis strategy

Data analysis is grounded in principles of generalizability theory (e.g., Brennan 2001; Cronbach et al. 1972; Shavelson and Webb 1991). The Pearson correlation coefficient (which is not a squared statistic) can be identical to a generalizability coefficient (which typically is a squared statistic), as detailed by Traub (1994) and demonstrated empirically by Fan and Sun (2014). Conceptually, generalizability theory can enable considerations of the correlation between two parallel forms, x and x′ (Brennan 2010). In this study, the classroom observation and student survey measure are treated as two such parallel forms. The data are structured in a long form according to De Boeck et al.’s (2011) descriptions. The variable “score” lists all dichotomous item responses, and the variable “item” is scored 1 to 72; the codes 1 to 32 identify scores on items of the classroom observation instrument, and codes 33 to 72 identify scores on the items of the student survey. Furthermore, the variable observer lists the codes related to classroom observers as well as the codes related to student observers in the same column. The categorical variable method (M), coded 1 for observation items and 2 for survey items, makes it possible to separate them.

In all subsequent models, the estimates of the inter-method correlations reflect the ratio of the facet “teacher” (t) divided by the sum of the facets “teacher” (t) plus all facets contributing to error variance in either one of the methods:

$$ {r}_{tt\prime }=\frac{\sigma_{\left(\mathrm{teacher}\right)}^2}{\sigma_{\left(\mathrm{teacher}\right)}^2+\frac{\sigma_{\left(\mathrm{error}\ \mathrm{observation}\right)}^2}{n_{\mathrm{observations}}}+\frac{\sigma_{\left(\mathrm{error}\ \mathrm{student}\ \mathrm{survey}\right)}^2}{n_{\mathrm{student}\ \mathrm{survey}\mathrm{s}}}\ } $$
(1)

This correlation coefficient has two possible interpretations: It is the expected correlation between the survey and classroom observation methods, but it also is a generalizability coefficient. In the former interpretation, the teaching effectiveness latent variable is measured twice by two different methods, x and x′, and the coefficient indicates the extent to which scores obtained with one method are associated to the other. In the latter interpretation, the coefficient reflects the correlation between the weighted average composite score and each of the separate measures.

g-Study

The multivariate g-study specifies all possible random effects, given the data gathering design. Only the teacher and item facets are estimated as composite means over the two methods. The class, observer, and teacher × observer facets are split by method. The g-study equation is:

$$ {X}_{\mathrm{ctoi}}=\mu +{\sigma}_{(t)}^2+{\sigma}_{(i)}^2+M{\sigma}_{(c)}^2+{M\sigma}_{(o)}^2+{M\sigma}_{(to)}^2+{M\sigma}_{(ic)}^2+{M\sigma}_{(it)}^2+{M\sigma}_{(io)}^2 $$
(2)

Table 1 lists all the random effects and their interpretation.

Table 1 List of all random effects included in the multivariate g-study and subsequent d-studies and their proposed interpretation
Full size table

d-Studies

The obtained variances then inform four d-studies. In all d-studies, the item facet (I) is fixed, to make the estimation more consistent with an item response theory (IRT) measurement model (Briggs and Wilson 2007; Choi 2013; Glas 2012). Previous researchers have routinely applied IRT measurement models to estimate teacher effects with these instruments (e.g., Maulana et al. 2015; van de Grift et al. 2014; van der Lans et al. 2015, 2017, 2018).

Finally, four d-studies provide estimations of the association between methods for four different combinations of classroom observation designs and survey designs. The models estimate the parameter rtt′, which designates the correlation (r) between t (teaching effectiveness estimates of the observation design) and t′ (teaching effectiveness estimates of the student survey design).

Model 1

The first d-study models the nested–nested combination without observer effects. A nested design implies that each class is matched with only one teacher, such that teacher and class variance are confounded. Teachers receive multiple visits by different classroom observers, but the model assumes zero observer effects, which implies that both students and observers score teachers using identical norms. The model assumptions are unrealistic; however, this model is of interest, because it presents a baseline for comparison. Model 1 is as follows:

$$ {r}_{tt\prime }=\frac{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2+{\sigma}_{\left(\mathrm{c},\mathrm{m}2\right)}^2}{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2+{\sigma}_{\left(c,\mathrm{m}2\right)}^2+\frac{\sigma_{\left( to,\mathrm{m}1\right)}^2}{n_{\mathrm{o}}}+\frac{\sigma_{\left( to,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}+\left(\frac{\sigma_{\left( Ic,\mathrm{m}1\right)}^2+{\sigma}_{\left( It,\mathrm{m}1\right)}^2}{n_{i,\mathrm{m}1}}\right)+\left(\frac{\sigma_{\left( Ic,\mathrm{m}2\right)}^2+{\sigma}_{\left( It,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}}\right)+\frac{\raisebox{1ex}{${\uppi}^2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{n_i{n}_o{n}_{\mathrm{s}}}} $$
(3)

Model 2

The second d-study models the nested–nested combination with observer effects. This nested combination implies that in both the classroom observation and survey design, each teacher is matched to one class, and the class and teacher effects are confounded. In the classroom observation design, teachers receive multiple visits by different classroom observers, but Model 2 also accounts for differences in classroom observer norms, as well as

the impact of differences in student observer norms. Model 2 is as follows:

$$ {r}_{t{t}^{\prime }}=\frac{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2+{\sigma}_{\left(c,\mathrm{m}2\right)}^2}{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2+{\sigma}_{\left(c,\mathrm{m}2\right)}^2+\left(\frac{\sigma_{\left(o,\mathrm{m}1\right)}^2+{\sigma}_{\left( to,\mathrm{m}1\right)}^2}{n_o}\right)+\left(\frac{\sigma_{\left(o,\mathrm{m}2\right)}^2+{\sigma}_{\left( to,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}\right)+\left(\frac{\sigma_{\left( Ic,\mathrm{m}1\right)}^2+{\sigma}_{\left( It,\mathrm{m}1\right)}^2}{n_{i,\mathrm{m}1}}\right)+\left(\frac{\sigma_{\left( Ic,\mathrm{m}2\right)}^2+{\sigma}_{\left( It,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}}\right)+\frac{\raisebox{1ex}{${\uppi}^2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{n_i{n}_o{n}_{\mathrm{s}}}\ } $$
(4)

Model 3

The third d-study models a nested–partially nested combination of designs. The classroom observation design is nested, such that each teacher is matched with a unique class. Teachers receive multiple lesson visits by different classroom observers. In addition, differences in classroom observer norms are taken into account. Unlike Model 2 however, multiple teachers are matched to one class. The survey design is partially nested, and the teacher and class facets are no longer confounded. Differences in student observer norms are taken into account. Model 3 is as follows:

$$ {r}_{t{t}^{\prime }}=\frac{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2}{\sigma_{(t)}^2+{\sigma}_{\left(c,\mathrm{m}1\right)}^2+\left(\frac{\sigma_{\left(o,\mathrm{m}1\right)}^2+{\sigma}_{\left( to,\mathrm{m}1\right)}^2}{n_o}\right)+\frac{\sigma_{\left(o,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}+\frac{\sigma_{\left( to,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}+\left(\frac{\sigma_{\left( Ic,\mathrm{m}1\right)}^2+{\sigma}_{\left( It,\mathrm{m}1\right)}^2}{n_{i,\mathrm{m}1}}\right)+\frac{\upsigma_{\left( Ic,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}{n}_{\mathrm{c}}}+\frac{\upsigma_{\left( It,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}}+\frac{\raisebox{1ex}{${\uppi}^2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{n_i{n}_{\mathrm{c}}{n}_o{n}_{\mathrm{s}}}} $$
(5)

Model 4

The final d-study models the correlations for a partially nested–partially nested combination of designs. In the classroom observation design, multiple teachers are matched to one class. Moreover, teachers receive multiple visits by different classroom observers, and the model takes variation in classroom observers’ norms into account. The survey design also matches multiple teachers with one class. Differences in student observer norms are addressed too. Model 4 is as follows:

$$ {r}_{tt\prime }=\frac{\sigma_{(t)}^2\ }{\sigma_{\left(\mathrm{t}\right)}^2+\frac{\sigma_{\left(o,\mathrm{m}1\right)}^2}{n_{\mathrm{o}}}+\frac{\sigma_{\left(o,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}+\frac{\upsigma_{\left( to,\mathrm{m}1\right)}^2}{n_{\mathrm{o}}}+\frac{\upsigma_{\left( to,\mathrm{m}2\right)}^2}{n_{\mathrm{s}}}+\frac{\sigma_{\left(\mathrm{Ic},\mathrm{m}1\right)}^2}{n_{i,\mathrm{m}1}{n}_{\mathrm{c}}}+\frac{\sigma_{\left( Ic,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}{n}_{\mathrm{c}}}+\frac{\sigma_{\left( It,\mathrm{m}1\right)}^2}{n_{i,\mathrm{m}1}}+\frac{\sigma_{\left( It,\mathrm{m}2\right)}^2}{n_{i,\mathrm{m}2}}+\frac{\raisebox{1ex}{${\uppi}^2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{n_i{n}_{\mathrm{c}}{n}_o{n}_{\mathrm{s}}}\ } $$
(6)

To cross-validate the model-estimated correlation coefficients, a further comparison evokes results reported previously by Howard et al. (1985), Maulana and Helms-Lorenz (2016), Murray (1983), and Van der Lans (2017).

4 Results

Table 2 provides the variance estimates for each of the facets and their respective standard errors. The observer facet suggests that the students’ scores are affected by their personal norms of good teaching, to a greater extent than trained observers’ are, which is logical given the difference in training. Furthermore, the teacher × observer facet shows more variation in the classroom observation measure than the student survey measure, which again makes sense; scores on classroom observation measures should vary over lessons and teacher–observer combinations (e.g., Charalambous et al. 2017; Praetorius et al. 2014), whereas scores on student survey measures are expected to be more lesson-generic and vary mostly over teacher–student combinations.

Table 2 Variance components analysis of the g-study
Full size table

The class effects possibly reflect differences in teachability of classes. Similar to Lei et al. (2018), the results of this study indicate that variance in class effects is nearly as large as the variance in teacher effects. This indicates that classroom observation scores of the same teacher may vary considerably between two classes. For the survey measure a slightly smaller, but still relatively large, variance in class effects is found.

Figure 2(1–4) portrays the results of the d-studies graphically. All models indicate that the correlation between the classroom observations and student survey scores increases with an increasing number of observers, in support of hypothesis 1. The difference is considerable; all models predict that correlations may double or even triple in size.

Fig. 2
figure 2

Expected correlation between classroom observation and student survey measures for different study designs

Full size image

The difference between Models 1 and 2 demonstrates how the observer effect attenuates the correlation. The observer effect reflects the observer’s personal norms and beliefs about what good teaching entails. Because the observer effect reflects the observer’s subjective norms about good teaching, which are unrelated to true teaching effectiveness, the observer effect is expected to lower the correlation. However, its impact is relatively small. Only if the number of students and observers approximates one does the observer effect notably impact on correlation size, i.e., with approximately 0.10 points. In realistic scenarios, with at least 20 students and one classroom observer, the observer effect exerts an impact no larger than 0.04–0.05 points on the correlation scale (Fig. 2(1 and 2)). Students’ observer effects bias the correlations by 0.02 points; classroom observers’ observer effects account for the rest of the 0.02–0.03 point decrease. The greater impact of classroom observers’ observer effect, despite its smaller variance (Table 2), supports the argument that the students’ greater observer effects are compensated for by their quantity (Marsh 2007).

Hypothesis 2 states that implementing a partially nested design affects the correlation, because in a partially nested design, the teacher and class effects are no longer confounded. The comparison of Model 2 with Models 3 and 4 shows that the correlation decreases substantially, ranging between 0.15 (20 or more students and one observer) and 0.20 (20 or more students and three observers) points on the correlation scale. The class effects of classroom observation and of the student survey measure must thus correlate positively. That is, teachers teaching certain classes receive higher (or lower) scores on the classroom observation and student survey measures than these same teachers would have received if they were to teach other classes. This result fits with an interpretation of class effects as mostly reflecting differences in teachability.

Relative to prior research, Model 2 approximates Murray’s (1983) and Martínez et al.’s (2016) designs. Murray applies strict sampling procedures, with the same six to eight observers visiting three different lessons by one teacher. Thus, Murray’s design repeatedly used the same observers, and his results should approximate the results of Model 2. Murray reports a correlation of 0.76, and Model 2 broadly corroborates this number: It estimates a correlation for seven observers (average of six and eight) of 0.74, for an average class size of 25. However, recall that Model 2 indicates the correlation when seven observers visit seven different lessons, whereas Murray’s (1983) study design involved three different lessons. In a comparison with three lesson visits (by three different observers), Model 2 predicts correlations of 0.60. In sum, the correlation predicted by model 2 likely is somewhat lower than Murray’s (1983) reported correlation and somewhere within the range of 0.60–0.74.

Other research has reported correlations for designs of one observer visiting one lesson (van der Lans 2017, r = 0.26; Maulana and Helms-Lorenz 2016, r = 0.26) and the same observer visiting two lessons (Howard et al. 1985, r = 0.24). Note that Howard et al.’s design does not overlap with any of the studied designs, which complicates the comparison. With respect to the class and teacher facets, the designs frequently show cross-classifications. For example, Maulana and Helms-Lorenz (2016) study a sample of 108 teachers rated by 98 classes, and Van der Lans (2017) study a sample in which 148 teachers were rated and observed in 98 different classes. The samples of both these studies must have contained a subset of classes that rated multiple teachers (partially nested design), whereas another part of the sample contained teachers matched with a unique class (nested design). The reported correlation thus results from a mix of completely nested and partially nested data, and Models 2, 3, and 4 should approximate the range of correlations observed. At the highest value, Model 2 predicts correlations of 0.35, and at the lowest, Model 4 predicts correlations of 0.19 for an average class size of 25 students.

All correlations are estimated with respect to the instrument total scores. Correlations of subscales likely vary around these numbers. Furthermore, correlations depend on the psychometric quality of the instruments (van der Lans 2017). Thus, the association may vary for different combinations of survey and observation instruments.

5 Discussion

This study explores whether the correlation between observation and survey measures depends on the study design. The results indicate a substantial effect of the number of classroom observations. If one observer visits a single lesson, the expected correlation is somewhere between 0.19 (Model 4) and 0.35 (Model 2), but if three observers each visit another lesson, this correlation approximately doubles (0.39 [Model 4] to 0.60 [Model 2]). One interpretation of this result is that gathering multiple observations of multiple lessons not only increases reliability but also potentially doubles (correlation-type) effect sizes.

Models 3 and 4 provide further support for the idea that the correlation between survey and classroom observation measures depends on the applied survey and observation designs. The predicted correlation dropped 0.15–0.20 points for partially, instead of completely, nested study designs. In the partially nested design, multiple teachers get observed and rated by the same class. The substantial difference between completely nested and partially nested designs with regard to reported correlations indicates the need for more precise descriptions of study designs that use classroom observation or survey measures. The apparent positive bias inherent in the nested design also warrants further attention; this positive bias could affect correlations between other variables (see also the discussion by Martínez 2012).

5.1 Contributions to research

This study pursues a new direction to investigate correlations between instruments. Generalizability theory typically has functioned to estimate the reliability of scores obtained in parallel measurement conditions (Brennan 2010). This study extends such applications of generalizability theory to explore whether correlations between two parallel measures of teaching effectiveness depend on their study designs. The possibility to use generalizability theory to predict fluctuations in associations between variables was already discussed by Kane and Brennan (1977) and empirically demonstrated by Fan and Sun (2014). It has also been used extensively by social psychologists such as in David Kenny’s PERSON model (e.g., Kenny (2004). This extension opens up the possibility to explore how associations between variables increase or decrease due to different implementations of data gathering procedures, which could inform policy decisions about how to organize evaluation systems and give researchers insights for choosing among competing study designs.

Two interpretations of the resulting generalizability coefficient are possible. It is the expected correlation between the survey and classroom observation methods, but it also is a reliability coefficient. The latter interpretation is valid only if it is reasonable to assume that measures are randomly parallel (Brennan 2010), such that apart from the (nonrandom) dependencies accounted for by the model, survey and classroom observation scores can be assumed to vary randomly around their mean scores. However, the former interpretation of the generalizability coefficient as a correlation coefficient has received much less attention. Evidence shows that Pearson correlations between two measures are identical to the generalizability coefficient (Fan and Sun 2014), and an assumption of parallelism is not required for the Pearson correlation. According to Brennan (2001) the generalizability coefficient technically is “a stepped-up intra class correlation (ICC) coefficient” (p. 35) and the ICC assumes parallelism between measures. In sum then, it is not clear whether the validity of this interpretation depends on an assumption of random parallel forms. Evidence based on Item Response Theory (IRT) indicates that the particular measures studied here are, by approximation, two random parallel measures of the same construct (van der Lans 2017), but caution is warranted before generalizing the analysis technique to research situations that involve nonparallel measures or measures that operationalize different constructs.

A second contribution of this research stems from the estimation of composite effects. The estimation of teacher composite effects using a random-effects generalizability theory approach deviates from previously applied estimation strategies based on fixed regression weights (e.g., Martínez et al. 2016; Mihaly et al. 2013). Fixed weights generally focus on sample average corrections based on some set of predictor variables (e.g., indicators of socioeconomic status, school achievement), whereas the random weights applied herein provide more individual-specific corrections based on consistencies and inconsistencies in the evaluation scores of the same teacher over different raters, lessons, and classes. Because evaluation involves individuals, the random-effects model approach has an advantage. Nevertheless, valid arguments could be made to justify fixed corrections for differences in students’ socioeconomic status and level of school achievement. Thus, it seems logical to pursue a mixed-effects model approach, combining the strengths of both fixed and random approaches. Central to this mixed approach is the notion that the correlation between two measures (or the reliability of the composite measure) must be high before fixed corrections can be implemented effectively (Kolen and Brennan 2013). In this reasoning, the random-effects part of the mixed model should be sufficiently complex to increase correlations to an appropriate level before the fixed weights enter the equation.

5.2 Possible caveats to the correlational approach: the surrogation fallacy

As mentioned previously, the main drawback of the analysis strategy taken by Martínez et al. (2016) motivated this study to adopt a slightly different correlational strategy based on random effects. However, the correlational approach also has limitations. Kane and Case (2004) discuss the meaning of a strong association between two measures and note the “fallacy of statistical surrogation” (Scriven 1987, p. 11). Kane and Case (2004, p. 225) explain the fallacy as follows: “It is important to note that just as correlation does not imply causality, even a perfect correlation does not imply that the measures have the same meaning.” Thus, the high correlations (r > 0.50) observed when the number of classroom observations increases might indicate that classroom observation and survey measures measure the same construct; however, they also might indicate that the survey and classroom observation measures refer to two different but closely associated constructs. Additional research should investigate this possibility further.

5.3 Implications for policy

Classroom observation and student survey instruments increasingly serve to monitor teaching effectiveness and make decisions about professionalization efforts (e.g., Isoré 2009; Martínez et al. 2016; NCTQ 2013). In light of these developments, as Martínez et al. (2016) assert, an appropriate emphasis on the measurement aspects of teacher evaluation is critical, because it is increasingly important that inferences about teachers are valid, fair, and useful for supporting professional development. The current study provides some recommendations along these lines. The number of classroom observations by different observers not only increases reliability but also may increase validity, as defined by the correlation with student surveys. Evaluation systems that do not implement multiple classroom observations risk creating a situation in which surveys and observations communicate different professionalization goals to teachers. Another recommendation would be to vary the classes in which teachers are surveyed and observed deliberately. Generally, policy makers aim to make inferences about a stable component of teaching effectiveness. If all measures relate to the same class, the variance attributable to the stable component may be biased upward, because it includes the stable characteristics of the class, as well as the teacher.

Finally, a potential fallacy would be to interpret the rather high correlations as suggestions that one of the measures is redundant. For example, if student surveys and classroom observations share high correlations, from an economic perspective, it may seem cost efficient to drop one of them. As discussed, such a claim would not necessarily be correct from the methodological point of view; but perhaps even more important, the use of multiple measures is justifiable on grounds other than statistical ones. For example, teachers may have more confidence in feedback and evaluations based on classroom observations, which warrants their use.

5.4 Limitations

This study has several limitations. The sample composition is dominated by male teachers, which is not representative of the Netherlands, where the teaching profession is dominated by women. No indications that the unequal gender distribution influenced the results were observed, but a replication using a more representative sample is advisable. In addition, the study explores the correlation between one survey and one classroom observation instrument, and the study conclusions do not necessarily generalize beyond these two instruments. Finally, the study could not estimate how correlations would change if the same observer were to visit multiple lessons of the teacher, which renders a valid comparison with Howard et al. (1985) virtually impossible. Additional research could add further complexity to the data gathering procedures, such as by incorporating designs in which multiple observers each visit a teacher on multiple occasions.

5.5 Back to Spearman

As stated in the introduction, the present study is believed to be a continuation of Spearman’s work (Spearman 1904), in that it highlights systematic errors that decrease or increase the reported correlations between survey and classroom observation measures. This line of inquiry is important, because both researchers and evaluators routinely interpret and use survey and classroom observation data as if they measure the same “thing.” To illustrate, studies measuring teaching effectiveness using survey methods and those measuring it using classroom observation methods both may be acceptable for publication (Maulana et al. 2015; van de Grift et al. 2014). Moreover, evaluators may use either student survey or classroom observation measures to indicate differences in teaching effectiveness (e.g., Kane et al. 2012; Marzano and Toth 2013). However, when it comes to their association, researchers and policy makers generally accept that the outcomes of survey and observation measures are more different than similar. In this acceptance, it seems as if we have given up on the possibility that they actually might share high correlations. This study ideally will contribute to the field by revealing the “plausibility of association.” The results send the positive message that perhaps the associations between observation and survey measures can be greater than at least some researchers currently allow themselves to hope.