Dedekind–MacNeille Completion of n-ordered Sets

Abstract

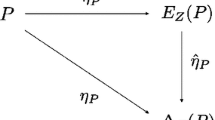
A completion of an n-ordered set ${\mathbf{P}}{\text{ = }}{\left\langle {P, \lesssim _{1} , \ldots , \lesssim _{n} } \right\rangle }$ is defined, by analogy with the case of posets (2-ordered sets), as a pair ${\left\langle {e,{\mathbf{Q}}} \right\rangle }$, where Q is a complete n-lattice and $e{\text{:}}{\mathbf{P}} \to {\mathbf{Q}}$ is an n-order embedding. The Basic Theorem of Polyadic Concept Analysis is exploited to construct a completion of an arbitrary n-ordered set. The completion reduces to the Dedekind–MacNeille completion in the dyadic case, the case of posets. A characterization theorem is provided, analogous to the well-known dyadic one, for the case of joined n-ordered sets. The condition of joinedness is trivial in the dyadic case and, therefore, this characterization theorem generalizes the uniqueness theorem for the Dedekind–MacNeille completion of an arbitrary poset.