Abstract
In this paper, we propose a device generating Bessel beam that can assist microscope to enhance resolution of microscope to λ/3. As the conventional optical devices of generating Bessel beam have some drawbacks, such as low efficiency, and bulky volume, we design plane-axicons for generating Bessel beam using the principle of phase superposition. The designed plane-axicons can generate Bessel beams with zero-order and higher-order by changing topological charge n. We also demonstrate the FWHMs of plane-axicons about as small as λ/3 and have FWHMs with weak fluctuations independent of wavelength across the visible spectrum, which means the Bessel beam can be used to increase resolution of microscope. These performances make the plane-axicons can also enable other advanced research and applications related to Bessel beams ranging from laser fabrication to optical manipulation.
Similar content being viewed by others
1 Introduction
The diffraction limit is always a problem to be solved in many optical imaging system, including optical microscope, one of the indispensable instruments for modern scientific research. However, the diffraction barrier limits the imaging resolution of microscopes to λ/2 leaving many subjects unresolvable (Wang et al. 2011; Cang et al. 2015). In recent years, many methods have intended to break optical diffraction barrier. For example, the microsphere lens, a special micro-lens with thinner full width at half maximum (FWHM), can assist microscope to realize super resolution imaging, but it can limit the imaging field of view because the size of the spherical microlens is about micron scale and have no methods to solve the problem at present (Lecler 2019; Huszka and Gijs 2018; Chen et al. 2018). Structured illumination microscopy can double the resolution of a microscope by manipulating the illumination pattern used, however, the method needs to acquire several to many images, as well as specialized illumination, fluorescent tags, or both in order to reconstruct higher resolution information (Kner et al. 2009; Wu and Shroff 2018; Dan et al. 2013; Gustafsson 2005). While the utility of these methods is unquestionable, they indeed exist their own drawbacks. Actually, Bessel beam, a non-diffracting beam, can realize super-resolution imaging to break through the diffraction limit because of its special physical structure. In the case of the same aperture and focusing position, the axicon lens can achieve the super-diffraction focusing (Durnin 1987). This is realized by modulating the point spread function using optical device that is a special optical phase device to generate Bessel beam. Because the structure of Bessel beam assist microscope to enhance resolution is relatively simple and the change for original imaging system is less relatively few, it can be conveniently applied to various occasions. The intensity of the secondary sidelobe of the spot increases when the FWHM of the principal maximum focusing spot decreases, and the image point would produce intensity distribution of water ripple. However, the sidelobe cannot influence the normal resolution and imaging because the intensity of the principal maximum is significantly stronger than secondary sidelobe’s. Besides the super-resolution imaging, the higher-order Bessel beams also have most potential research topic in the optical and quantum communication fields as it carries orbital angular momentum (OAM) with a large amount of coding information (Shi and Zhang 2018; Meng et al. 2019; Yu et al. 2016).
Generally, the Bessel beam can be generated by the axicon (Scott and McArdle 1992), annular gap lens (Durnin et al. 1987), and spatial light modulator (Mphuthi et al. 2019), however, these all methods have their drawbacks, such as too bulky volume to integrate, implementing inefficiency, high requirements for devices and so on. Metasurface, consisting of subwavelength nanostructures, can produce many extraordinary properties from the designed subwavelength phase shifters with electromagnetic responses based on the generalized Snell’s law (Yu et al. 2011), thus the metasurfaces can realize many devices with fantastic functions (Zhang and Yang 2019; Liu et al. 2020; Hu et al. 2019; Phan et al. 2019; Zeng et al. 2013; Klar et al. 2000) which are impossible for the conventional optical elements. For example, A. Farmani and A. Mir et al., demonstrated tunable mantle cloaking (Zarghani et al. 2019; Zhang et al. 2019), absorber (Moradiani et al. 2020),Optical nanosensors (Mozaffari and Farmani 2020; Amoosoltani et al. 2020; Farmani and Mir 2020; Farmani et al. 2020), and so on. Li and Shi et al. demonstrated the vortex beam generated by the metamaterial or metasurface in the radio frequency domain or THz band (Shi and Zhang 2018; Meng et al. 2019; Yu et al. 2016), Yuan also generated vortex beam by metasurface (Yuan et al. 2017), which is promising to be usedradio and microwave wireless communication applications. Some polarization-independent structures also generated by the metasurface (Parmar et al. 2020; Patel et al. 2020a, 2020b; Xin et al. 2020; Luan et al. 2020), but they regarded as absorber. Gao et al. researched to generate Bessel beam using the metasurface (Gao et al. 2017), but its work wavelength is in the microwave band, which limits its application. Capasso et al. generated Bessel beam using metasurface (Chen et al. 2017a), however, we adopted principle of phase superposition to realize Bessel beam, which opened up a novel way to design many complicated optical devices with metasurface. Obviously, more and more special beams can be achieved by novel structures based on the metasurface. Unlike conventional phase-modulating devices, the designed plane-axicons with metasurface have little volume and powerful features. Various applications, including (but not limited to) microscopy (Kwon et al. 2020), optical manipulation (Yoon et al. 2019; Liu et al. 2019; Guo et al. 2019) and lithography (Kamali et al. 2019; Dirdal et al. 2020), all require subwavelength FWHM to achieve high spatial resolution, strong trapping force and subwavelength feature sizes, respectively.
In this paper, an optical device generating Bessel beam is proposed to enhance resolution of microscope, this make the conventional microscope resolution is 0.65 times of the Rayleigh criterion compared with conventional microscope. Then we design plane-axicon for generating Bessel beams based on the principle of phase superposition by superposing phase abrupt variable of the zeroth-order Bessel beam and Vortex beam, which overcomes drawbacks of conventional devices and provides us an effective methods to design others complex optical devices. Simultaneously, we analyse the phase of Bessel beam with different topological charge (n) values and the FWHMs of the J0 and J1 Bessel beam are investigated by FDTD solutions, and the intensity, phase, and FWHMs of beams are identical and with weakly fluctuation, which verifies the property of not-divergent in the propagation direction of the Bessel beams and capability of super-resolution focusing. At last, the FWHMs of the Bessel beams with different incident wavelengths are simulated, and the results indicate that FWHMs of the Bessel beams generated by our plane-axicons are independent of the wavelength.
2 Design and simulation
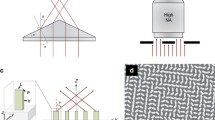
Figure 1a shows working principle diagram of our proposed that Bessel beam assist conventional microscope to enhance resolution. Compared with conventional microscope, two optical devices are integrated between the objective lens and eyepieces or CCD camera. The first is a convex lens placed away from the imaging plane of the microscope, the other lens is our designed plane-axicon. This combination transforms the wavefront of a point source into a Bessel beam, which is known for its ability to propagate without diffracting. The image plane of conventional microscope can be reprocessed to realize super-resolution imaging, the diagram of Bessel beam imaging is shown in the Fig. 1b. The objective plane in the Fig. 1b is the image plane of conventional microscope in the Fig. 1a, and the function of convex lens is converting waves from different points expressed in different colors in the Fig. 1b into a series of plane waves. This plane waves are super-diffracted and focused by a plane-axicon to achieve super-resolution imaging. When the Bessel beam is imaged by a CCD camera, the results \(\delta_{min}\) in the resolution of super-resolution microscope can be given (Snoeyink and Wereley 2013):
where NA is number aperture of microscope, Eq. (1) is similar to the diffraction-limited resolution (\(d_{m} = 0.61{\uplambda }/{\text{NA}}\)) of a conventional microscope by the Rayleigh criterion, but with a coefficient of 0.3828 as opposed to 0.61, which implies that the super-resolution microscope reduces the minimum resolvable feature size by at least one third. Obviously, the Bessel beam can realize super-resolution imaging, thus it need an optimal optical device to generate Bessel beam and overcome drawbacks of conventional devices. So we design a plane-axicon based on the metasurface with plane structure.
In our design, the building blocks of plane-axicon are titanium dioxide (TiO2) nanofins and SiO2 substrate, and the element structure is a single nanofin and they are arranged according to the certain rules. Under circularly polarized light illumination, the plane-axicon could focus into Bessel beams with helical form. Figure 2a shows the basic elements of the plane-axicon that deflects an incident collimated light to an angle β toward its center to generate Bessel beams, this phase shifter is identical rotated TiO2 nanofin arranged in a square lattice with period P, height H, length L and width W. Clearly, the phase profile \(\varphi \left( {x,y} \right)\) is discretely imparted because the unit cell size P of the nanofins is finite, actually, it can restrict the maximum achievable NA of the plane-axicon, which can be expounded by the Nyquist − Shannon sampling theorem in the spatial domain. To achieve the high NA, the period of unit cell size P must satisfy following condition: \(P \le \frac{{\uplambda }}{2NA}\) (Chen et al. 2017b), which cannot be satisfied by conventional diffractive elements (Leach et al. 2006; Escuti et al. 2016).
a Schematic 2D diagram of designed Plane-axicon. The Plane-axicon deflects an incident light to an angleβtoward its center to generate Bessel beams. The Plane-axicon is composed of identical TiO2 nanofins but different rotation angle with respect to its geometrical center. The Plane-axicon is designed at wavelength \(\lambda = 532nm\) with dimensions (L = 210 nm, W = 70 nm, H = 600 nm, P = 240 nm). b, c Maps of the transmission and phase of the unite cell as a function of the nanofin length and wavelength. d Transmittance and phase shift curves of the selected nanofin in the design. e The schematic of unit cell. θ is the each unit cell rotation degree to generate Bessel beam. f, g The transmission and phase shift curves of unit cell rotated angle 0, 15, 30, 45, 60, 75 and 90 degree. h Schematic view of designed plane-axicon model
Obviously, for the designed plane-axicon, the smaller element structure size P, the larger the achievable NA. In our designed plane-axicon, the period of unit cell size P is set 240 nm at wavelength 532 nm, which can obtain a maximum achievable theoretical NA. Obviously, the phase profile of plane-axicon can also be designed by varying the nanostructures with geometrical sizes (length, width or diameter and so on) pixel by pixel (Yu et al. 2011; Sun et al. 2012). In addition, to maintain the maximal efficiency at the designed wavelength λ, the single phase shifter’ size must meet the relation that increases the ratio of L to W or the height H, but thus would have constrained for the fabrication of metasurface. To achieve the optimal size of the element structure, the finite difference time domain (FDTD from Lumerical Inc.) method is used to calculate the transmission and phase of element structure, the PML boundary condition is used, mesh is set 0.001 and mesh accuracy is set 2. By sweeping the parameter length L with 0.02 nm step from 0.1 − 0.4 μm and wavelength λ with 0.2 nm step from 450 to 750 nm, we can gain the transmission and phase maps of the element structure in the Fig. 2b − c, then the transmissivity of the different length nanofins and different wavelengths were analyzed. The results indicate that the transmissivity is the optimal when the nanofin length is 210 nm. Figure 2d demonstrates the curve of the transmissivity and phase shift of the element structure with length of 210 nm. So in our case, the parameters of unit cell size are designed: L = 210 nm, W = 70 nm, H = 600 nm, and P = 240 nm, respectively.
Then to achieve the plane-axicon, we analyses phase distribution of Bessel beam firstly. Obviously, the Bessel beam phase is complex and can be decomposed into many simple and common phases, then the principle of phase superposition can be used to design the plane-axicon. According to the principle of phase superposition, the phase distribution of element structure at each position of designed plane-axicon that can be divided to the phase profile of the zero-order Bessel beams and vortex beams. The Eq. (2) \(\varphi_{1} \left( {x,y} \right)\) (Gao et al. 2017) is the phase abrupt variable should be introduced into the optical path of unit cell in position coordinates (x, y) for the zero-order Bessel beam, and \(\varphi_{2} \left( {x,y} \right)\) (Yuan et al. 2017) is phase abrupt variable should be introduced into the optical path of unit cell in position coordinates (x, y) for the vortex beams.
where β is the one-half of the top angle of Bessel beam generated by the design, n is topological charge number that describes the vortex beams with different OAM. Thus for generating Bessel beams, For the Bessel beam, the phase abrupt variable that should be introduced into the optical path by the unite cell at the position coordinates (x, y) is as follows Eq. (3):
The rotation angle of the nanofin \(\theta \left( {x,y} \right)\) needs to meet \(\theta \left( {x,y} \right) = \varphi \left( {x,y} \right)/2\) and MATLAB software is used to calculate accurately the rotation angle of each unite cell that need to provide phase compensation at each position (x, y) by the Eq. (3), Fig. 2e demonstrates the unit cell model and rotates angel θ, and Fig. 2f and g show the transmission and phase shift of the nanofin rotated angle 0, 15, 30, 45, 60, 75 and 90 degree. At our design, the plane-axicon is spherical with radius of 5 μm, and unite cell size L = 210 nm, W = 70 nm, H = 600 nm, and P = 240 nm. It means that the transmission efficiency of the unit cell can reach 80% approximately. And the nanofins can overlap 0 ~ 2π phase. Then the plane-axicon model shown in Fig. 2h can be built through rotating and translating the element structure (nanofin) in FDTD software. To maximize the performance of the plane-axicon, each nanofin should convert incident circularly polarized light to its orthogonal polarization state. We analyze the conversion efficiency using three-dimensional finite difference time domain method. At wavelength 532 nm, simulated polarization conversion efficiencies 55% were obtained. To determine the polarization conversion efficiency, PML boundary conditions were used. And efficiency drops with increasing incident wavelength. Additionally, the method of design plane-axicon provides us a novel way to design other complex optical devices.
3 Results and discussion
The Bessel beams carries the OAM with a large amount of coding information because of topological charge parameter n. Figure 3a − e shows the phase amplitude profiles of the Bessel beam with different topological charges at incident wavelength 532 nm. Figure 3 first row demonstrates the phase profiles of the Bessel beams by the theoretical method with the n value 0, 1, 2, −2, and 3, respectively. Clearly, the phase profile do not have helical phase gradient when the n value is 0 in Fig. 3a, which implies that the plane-axicon generates J0 Bessel beam and the phase profile satisfies the J0 Bessel beam. When the n value is 1, one helical phase gradient is generated in the phase profile and the J1 Bessel beam can be generated by the phase profile, simultaneously, this corresponding to Bessel beam carries a 1ћ OAM. When the n value continue to increase 2 and 3, the two and three helical phase gradients are discovered in the phase profiles in the Fig. 3c and e, actually, higher-order (J2 and J3) Bessel beams that carries 2ћ and 3ћ OAM can be generated. Specially, the n value is −2 in the Fig. 3d, which demonstrates that the helical phase gradient is converse with the n value is 2 and −2ћ OAM is carried. The second row shows the phase profiles by the FDTD solutions method corresponding with the first row, obviously, these results are very fit well with theoretical. Third row demonstrates the E-field amplitude profiles of the different order Bessel beams corresponding second row. Obviously, the blank space of center of focal spot is gradually increasing, which is which correspond to vortex waves carrying OAM in the n = 1, n = ± 2 and n = 3 modes, respectively. Through changing the parameter n value, we can achieve phase profiles of arbitrary-order Bessel beams with OAM information, which provides the foundation to design plane-axicons. It is worth noting that phase profiles of these plane-axicons also are designed by varying the geometrical sizes of the nanofins, pixel by pixel, so amplitude of each pixel has strong differences. This unwanted differences of amplitude of each pixel can lead to the deflection of light from multiple angles, thus would change the profile of the Bessel beams. However, as each nanofin is identical and has the same geometrical sizes, the differences of amplitude of each pixel can be minimized by our design method for all wavelengths in the case of circularly polarized illumination. Furthermore, in order to evaluate the mode purity of the OAM in the higher-order Bessel beams, we use the spectral analysis of Fourier transform (Jack et al. 2008). Figure 4a − c shows the mode purity of OAM at n = 1, n = ± 2, n = 3, and the phase of the OAM wave are sampled along the blue dotted circle perimeter. One can see that the spectral intensities of the dominant OAM modes including n = 1, n = ± 2, n = 3 are 72%, 68%, and 65%, respectively, which are much dominant than those of other modes, and thus good mode purity characteristic is obtained. Obviously, there are second aspects advantages compared with the ref. 37. First, the design method is different, the ref. 37 used the method that calculates the Bessel beam phase profile and to design, we used the method of phase superposition calculate the phase abrupt variable, then calculate the location and rotation degree by MATLAB and design. Our method provides a novel way to design more complex beams and complicated phase superposition devices based on metasurface. Second, the ref. 37 is only a device to generate Bessel beams, but our plane-axicon would to assist microscope to achieve super-resolution, therefore design parameters and performance are different.
a − e The phase and E-field amplitude profiles of the Bessel beams at incident wavelength 532 nm with different orders n: n = 0, n = 1, n = 2, n = -2, n = 3, respectively. The first row shows phase profiles with parameter n: n = 0, n = 1, n = 2, n = -2, n = 3, respectively, obtained by theoretical method. The second row shows phase profiles that are corresponding to the first row, obtained by simulations. The third row shows amplitude profiles that are corresponding to the second row, obtained by simulations
Then in order to testify the designed plane-axicons having ability of generating Bessel beams, the plane-axicons generating J0 J1, J2 and J3 Bessel beams are simulated, PML boundary condition were used and mesh accuracy is set 4. And the NA of plane-axicons are 0.7 and incident wavelength is 532 nm. The intensity and phase profiles of the J0, J1, J2 and J3 Bessel beams by simulated are demonstrated in the Fig. 5a − d at propagation direction Z = 2 μm, Z = 3 μm, Z = 4 μm and Z = 5 μm, respectively, clearly, the intensity and phases of Bessel beams have no large change at the propagation direction. The intensity curves of J0, J1, J2 and J3 Bessel beams (Fig. 5a − d) corresponding their horizontal cut are shown in the Fig. 5e, termed FWHMs. One can see that the FWHMs of the J0, J1, J2 and J3 Bessel beams are also identical at propagation direction. Lastly, the Fig. 5e demonstrate the FWHMs of J0 J1, J2 and J3 Bessel beams at different planes in all the propagation axis, obviously, the fluctuation of FWHMs is small and can be ignored. Therefore, Fig. 5 proves designed plane-axicons can generate Bessel beams with zero-order and higher-order because the intensity, phases and FWHMs of J0, J1, J2 and J3 Bessel beams are identical in the propagation direction.
a − d The intensity in the x − y plane and corresponding phase profiles of J0, J1, J2 and J3 Bessel beams at Z = 2 μm, Z = 3 μm, Z = 4 μm and Z = 5 μm planes along the propagation direction, respectively. e The intensity curves of J0, J1, J2 and J3 Bessel beams corresponding horizontal cut (a − d). f The FWHMs values for J0, J1, J2 and J3 Bessel beams along the propagation direction. The NA and incident wavelength are 0.7 and 532 nm, respectively
As the Bessel beam can assist microscope to realize super-resolution, the intensity of focusing plane and FWHM of J0, J1, J2 and J3 Bessel beams are investigated. Figure 6a − d shows the intensity profiles of the J0, J1, J2 and J3 Bessel beams along the propagation direction, respectively. Figure 6e − h shows the intensity curves of the J0, J1, J2 and J3 Bessel beams along a horizontal cut across centers of d − f, respectively. Then theoretical value of FWHMs of the Bessel beams can be achieved by electric field intensity formula of Bessel beam, FWHM of the J0 Bessel beam is defined as the distance between two points at half of the maxima intensity of the center bright spot, which can be expressed as following (Chen et al. 2017a):
where \(k_{r} = \left( {2\pi /\lambda } \right) \cdot NA\). Similarly, the FWHM of J1 Bessel beam is defined as twice the distance from the dark spot center to the point at its closest ring with the half maxima intensity, and given by (Chen et al. 2017a):
According to the Fig. 6e, the FWHM of the J0 Bessel beam is observed to be 254 nm with 3.50 nm standard deviation, which is very close to its theoretical limit of 272 nm (Eq. (4)). And the FWHM of the J1 Bessel beam is 221 nm with 2.15 nm standard deviation in the Fig. 6f, which agrees well with its theoretical value of 222 nm (Eq. (5)). The difference of simulation and theoretical calculation mainly comes from three aspects, the difference accuracy error of FDTD method, the reflection error of truncated boundary of FDTD method, and the accuracy of numerical calculation of computer itself. Therefore, this difference is allowed. Similarly, the FWHMs of J2 and J3 Bessel beams is 205 nm with 3.14 nm standard deviation and 189 nm with 2.56 nm standard deviation. Therefore, unlike conventional phase-modulating devices (for example, spatial light modulators), our designed plane-axicons can provide subwavelength spatial resolution, which can be used to assist microscope to enhance resolution.
Figure 7 shows FWHMs of (a) J0 and (b) J1 Bessel beam as a function of wavelength with different NA. Obviously, the much larger NA, the smaller FWHM. According to the Eqs. (4) and (5), the FWHMs of the Bessel beam are proportional to wavelength and varies accordingly. Therefore, the FWHM values of the Bessel beams is proportional to wavelength and varies accordingly with wavelength. For the conventional axicons generating Bessel beams, if changes the wavelength from 450 to 750 nm, the FWHM values of the Bessel beams can be lead to result in a difference of 175%. However, for the our designed plane-axicons, the FWHM values of Bessel beams for both J0 and J1 remarkably changed weakly with different wavelengths, the reason for this is that the designed plane-axicon has phase compensation that can be able to compensate for the wavelength dependence of Bessel beams, showing wavelength independent FWHM. As mentioned previously, the transverse intensity profile is determined by the factor \(k_{r} = \left( {2\pi /\lambda } \right) \cdot NA\). In our case, the \({ }NA = \frac{\lambda }{2\pi }\nabla \varphi \left( {x,y,\lambda } \right)\), where \(\varphi\) is Eq. (3). Therefore, kr only depends on the phase gradient \(\nabla \varphi \left( {x,y,\lambda } \right)\), in this case, the phase gradient is a constant. Therefore, the FWHMs of the Bessel beams are independent of the wavelength. The wavelength-independent performance of the plane-axicons also provide convenient to realize super-resolution imaging, especially for the microscopes that output beams of different wavelengths.
4 Conclusions
In summary, the plane-axicons generating Bessel beams were demonstrated to increase resolution of microscope. The phase superposition method is used to design plane-axicon based on metasurface, and it provides a novel method to design other complex optical devices. We calculated the phase of Bessel beams with different topological charge n by theoretical and stimulation methods, and the intensity and phase profiles of the J0 and J1 Bessel beams are shown at propagation direction, the results prove that the design plane-axicon can generate Bessel beam. The FWHMs of J0 and J1 Bessel beams are shown to be as small as 254 and 221 nm. In addition, the generated Bessel beams are shown wavelength independent property for incident light. Therefore, these performances of plane-axicon can be integrated in a conventional microscope to realize super-resolution imaging, moreover, the plane-axicons can be used not only in super-resolution imaging but also in other applications ranging from laser lithography and manipulation to optical communication.
References
Amoosoltani, N., Yasrebi, N., Farmani, A., Zarifkar, A.: A plasmonic nano-biosensor based on two consecutive disk resonators and unidirectional reflectionless propagation effect. IEEE Sens. J. 20(16), 9097–9104 (2020)
Cang, H., Salandrino, A., Wang, Y., Zhang, X.: Adiabatic far-field sub-diffraction imaging. Nat. Commun. 6(7942), 1–6 (2015)
Chen, W.T., Khorasaninejad, M., Zhu, A.Y., Oh, J., Devlin, R.C., Zaidi, A., Capasso, F.: “Generation of wavelength-independent subwavelength Bessel beams using metasurface” . Light: Sci. Appl. 6, e16259–e16259 (2017a)
Chen, W.T., Zhu, A.Y., Khorasaninejad, M., Shi, Z.J., Sanjeev, V., Capasso, F.: Immersion meta-lenses at visible wavelengths for nanoscale imaging. Nano Lett. 17, 3188–3194 (2017b)
Chen, L.W., Zhou, Y., Wu, M.X., Hong, M.H.: Remote-mode microsphere nano-imaging: new boundaries for optical microscopes. Opto-Electronic Adv. 1, 270001 (2018)
Dan, D., Lei, M., Yao, B.L., Wang, W., Winterhalder, M., Zumbusch, A., Qi, Y.J., Xia, L., Yan, S.H., Yang, Y.L.: DMD-based LED-illumination super-resolution and optical sectioning microscopy. Sci. Rep. 3, 1–7 (2013)
Dirdal, C.A., Jensen, G.U., Angelskar, H., Thrane, P.C.V., Gjessing, J., Ordnung, D.A.: Towards high-throughput large-area metalens fabrication using UV-nanoimprint lithography and Bosch deep reactive ion etching. Opt. Express 28(10), 15542–15561 (2020)
Durnin, J.: Exact solutions for nondiffracting beams. I. the scalar theory. J. Opt. Soc. Am. A 4, 651–654 (1987)
Durnin, J., Miceli, J.J., Eberly, J.H.: Diffraction-free beam. Phys. Rev. Lett. 58(15), 1499–1501 (1987)
Escuti, M.J., Kim, J., Kudenov, M.W.: Controlling light with geometric-phase holograms. Opt. Photon. News 27, 22–29 (2016)
Farmani, A., and Mir, A.: “Nanosensors for street-lighting system”, Nanosensors for Smart Cities in volume in Micro and Nano Technologies, Chap. 13, pp 209−225. Elsevier (2020)
Farmani, A., Soroosh, M., Mozaffari, M.H., Daghooghi, T.: “Optical nanosensors for cancer and virus detections”, Nanosensors for Smart Cities in volume in Micro and Nano Technologies, Chap. 25, pp 419−432. Elsevier (2020)
Gao, H., Pu, M.G., Li, X., Ma, X.L., Zhao, Z., Guo, Y.G., Luo, X.G.: Super-resolution imaging with a plane axicon lens realized by a geometric metasurface. Opt. Express 25(12), 13933–13943 (2017)
Guo, X.X., Ding, Y.M., Duan, Y., Ni, X.J.: Nonreciprocal metasurface with space–time phasemodulation. Light: Sci. Appl. 8, 1–9 (2019)
Gustafsson, M.G.: Nonlinear structured-illumination microscopy: wide-field fluorescence imaging with theoretically unlimited resolution. P. Natl. Acad. Sci. USA 102, 13081–13086 (2005)
Hu, G.W., Hong, X.M., Wang, K., Wu, J., Xu, H.X., Zhao, W.C., Liu, W.W., Zhang, S., Garcia-Vida, F., Wang, B., Lu, P.X., Qiu, C.W.: Coherent steering of nonlinear chiral valley photons with a synthetic Au–WS2 metasurface. Nat. Photon. 13, 467–472 (2019)
Huszka, G., Gijs, M.A.M.: Turning a normal microscope into a super-resolution instrument using a scanning microlens array. Sci. Rep. 8, 1–8 (2018)
Jack, B., Padgett, M.J., Arnold, S.F.: Angular diffraction. New J. Phys. 10(10), 103013 (2008)
Kamali, S.M., Arbabi, E., Kwona, H., Faraon, A.: Metasurface-generated complex 3dimensional optical fields for interference lithography. PNAS 116(43), 21379–21384 (2019)
Klar, T.A., Jakobs, S., Dyba, M., Egner, A., Hell, S.W.: Fluorescence microscope with diffraction resolution barrier broken by stimulated emission. Proc Natl Acad Sci USA 97, 8206–8210 (2000)
Kner, P., Chhun, B.B., Griffis, E.R., Winoto, L., Gustafsson, M.G.L.: Super-resolution video microscope of live cell by structured illumination. Nat. Methods 6, 339–342 (2009)
Kwon, H., Arbabi, E., Kamali, S.M., Faraji-Dana, M.S., Faraon, A.: Single-shot quantitative phase gradient microscopy using a system of multifunctional metasurfaces. Nat. Photon. 14, 109–114 (2020)
Leach, J., Gibson, G.M., Padgett, M.J., Esposito, E., McConnell, G.: “Generation of achromatic Bessel beams using a compensated spatial light modulator.” Opt. Express 14, 5581–5587 (2006)
Lecler, S., Perrin, S., Leong-Hoi, A., Montgomery, P.: Photonic jet lens. Sci. Rep. 9, 1–8 (2019)
Liu, Z.J., Xu, Y., Lin, Y., Xiang, J., Feng, T.H., Cao, Q.T., Li, J.T., Lan, S., Liu, J.: High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 123, 253901 (2019)
Liu, F., Guo, J.Y., Zhao, L.Y., Huang, G.L., Li, Y.S., Yin, Y.Z.: Dual-band metasurface-based decoupling method for two closely packed dual-band antennas. IEEE T. Antenn. Propag. 68(1), 552–557 (2020)
Luan, J., Yang, S., Liu, D.M., Zhang, M.M.: Polarization and direction-controlled asymmetric multifunctional metadevice for focusing, vortex and Bessel beam generation. Opt. Express 28(3), 3732–3744 (2020)
Meng, Z.K., Shi, Y., Wei, W.Y., Zhang, Y., Li, L.: Graphene-based metamaterial transmit array antenna design for generation of tunable orbital angular momentum vortex. Opt. Mat. Express 9(9), 3709–3716 (2019)
Moradiani, F., Farmani, A., Yavarian, M., Mir, A., Behzadfar, F.: A multimode graphene plasmonic perfect absorber at terahertz frequencies. Physica E 122, 114159 (2020)
Mozaffari, M.H., Farmani, A.: On-chip single-mode optofluidic microresonator dye laser sensor. IEEE Sens. J. 20(7), 3556–3663 (2020)
Mphuthi, N., Gailele, L., Litvin, I., Dudley, A., Botha, R., Forbes, A.: Free-space optical communication link with shape-invariant orbital angular momentum Bessel beams. Appl. Opt. 58(16), 4258–4264 (2019)
Parmar, J., Patel, S.K., Katrodiya, D., Nguyen, T.K., Skibina, J.S., Dhasarathan, V.: Numerical investigation of gold metasurface based broadband near-infrared and near-visible solar absorber. Phys. B 591, 412248(1) (2020)
Patel, S.K., Parmar, J., Trivedi, H., Zakaria, R., Nguyen, T.K., Dhasarathan, V.: Highly sensitive graphene-based refractive index biosensor using gold metasurface array. IEEE. Photonic Tech. L. 32(12), 681–684 (2020a)
Patel, S.K., Charola, S., Parmar, J., Ladumor, M., Ngo, Q.M., Dhasarathan, V.: Broadband and efcient graphene solar absorber using periodical array of C-shaped metasurface. Opt. Quant. Electron 52, 1–19 (2020b)
Phan, T.B., Sell, D., Wang, E.W., Doshay, S., Edee, K., Yang, J.J., Fan, J.A.: High-efficiency large-area topology-optimized metasurfaces. Light Sci Appl 8, 1–9 (2019)
Scott, G., McArdle, N.: Efficient generation of a nearly diffraction free beam using an axicon. Opt. Eng. 31(12), 2640–2643 (1992)
Shi, Y., Zhang, Y.: Generation of wideband tunable orbital angular momentum vortex waves using graphene metamaterial reflectarray. IEEE Access 6(1), 5341–5347 (2018)
Snoeyink, C., Wereley, S.: Single-image far-field subdiffraction limit imaging with axicon. Opt. Lett. 38(5), 625–627 (2013)
Sun, S.L., Yang, K.Y., Wang, C.M., Juan, T.K., Chen, W.T.: High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett 12, 6223–6229 (2012)
Wang, Z.B., Guo, W., Li, L., Lukyanchuk, B., Khan, A., Liu, Z., Chen, Z.C., Hong, M.H.: Optical virtual imaging at 50nm lateral resolution with a white-light nanoscope. Nat. Commun. 2, 1–6 (2011)
Wu, Y., Shroff, H.: Faster, sharper, and deeper: structured illumination microscopy for biological imaging. Nat. Methods 15, 1011–1019 (2018)
Xin, M.G., Xie, R.S., Zhai, G.H., Gao, J.J., Zhang, D.J., Wang, X., An, S.S., Zheng, B., Zhang, H.L., Ding, J.: Full control of dual-band vortex beams using a high-efficiency single-layer bi-spectral 2-bit coding metasurface. Opt. Express 28(12), 17374–17383 (2020)
Yoon, G., Jang, J., Mun, J., Nam, K.T., Rho, J.: Metasurface zone plate for light manipulation in vectorial regime. Commun. Phys. 2, 1–8 (2019)
Yu, N.F., Genevet, P., Kats, M.A., Aieta, F., Tetienne, J.P., Capasso, F., Gaburro, Z.: Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334(6054), 333–337 (2011)
Yu, S.X., Li, L., Shi, G.M., Zhu, C., Zhou, X.X., Shi, Y.: “Design, fabrication, and measurement of reflective metasurface for orbital angular momentum vortex wave in radio frequency domain". Appl. Phys. Lett. 108, 121903 (2016)
Yuan, Y.Y., Ding, X.M., Zhang, K., Wu, Q.: Planar efficient metasurface for vortex beam generating and converging in microwave region. IEEE Trans. Magn. 56(6), 1–4 (2017)
Zarghani, Z.H., Yahaghi, A., Matekovits, L., Farmani, A.: Tunable mantle cloaking utilizing graphene metasurface for terahertz sensing applications. Opt. Express 27(24), 34824–34827 (2019)
Zeng, C., Liu, X.M., Wang, G.X.: Electrically tunable graphene plasmonic quasicrystal metasurfaces for transformation optics. Sci. Rep. 3, 1–8 (2013)
Zhang, Y.C., Yang, X.D., Gao, J.: “Generation of polarization singularities with geometric metasurfaces.” Sci. Rep. 9, 1–10 (2019)
Acknowledgements
This research was supported by the National Natural Science Foundation of China (61377007, 61575152 and 61775174).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Xiaorui Wang: The Fundamental Research Funds for the Central Universities (20101186553) and the 111 Project (B17035).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, D., Wang, X., Ling, J. et al. Planar efficient metasurface for generation of Bessel beam and super-resolution focusing. Opt Quant Electron 53, 143 (2021). https://doi.org/10.1007/s11082-021-02765-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-021-02765-7