Skip to main content
SpringerLink
Log in

Dispersive bright, dark and singular optical soliton solutions in conformable fractional optical fiber Schrödinger models and its applications

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

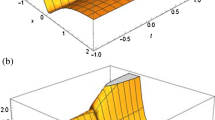
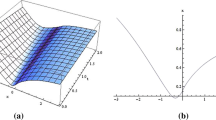
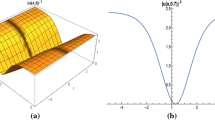
In this paper, we study three different space-time fractional models of the Schrödinger equation. By using the properties of conformable derivative and fractional complex transform, the bright, dark and singular optical solitons for conformable space–time fractional nonlinear \((1+1)\)-dimensional Schrödinger models are determined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abdeljawad, T.: On conformable fractional calculus. J. Comput. Appl. Math. 279, 57–66 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  • Abdullaha, A., Seadawy, A.R., Jun, W.: Mathematical methods and solitary wave solutions of three-dimensional Zakharov–Kuznetsov–Burgers equation in dusty plasma and its applications. Results Phys. 7, 4269–4277 (2017)

    Article  ADS  Google Scholar 

  • Agrawal, G.P.: Nonlinear fiber optics: its history and recent progress [Invited]. J. Opt. Soc. America B 28, A1–A10 (2011)

    Article  ADS  Google Scholar 

  • Arshad, M., Seadawy, Aly R., Lu, Dianchen: Exact bright-dark solitary wave solutions of the higher-order cubic-quintic nonlinear Schrödinger equation and its stability, Optik 128, 40–49 (2017)

    Article  ADS  Google Scholar 

  • Darvishi, M.T., Ahmadian, S., Baloch Arbabi, S., Najafi, M.: Optical solitons for a family of nonlinear (1+1)-dimensional time-space fractional Schrödinger models. Opt. Quantum Electron. 50, 1–20 (2018)

    Article  Google Scholar 

  • Eslami, M., Rezazadeh, H., Rezazadeh, M., Mosavi, S.S.: Exact solutions to the space-time fractional Schrödinger-Hirota equation and the space-time modified KDV-Zakharov-Kuznetsov equation . Opt. Quantum Electron. 49, 1–13 (2017)

    Article  Google Scholar 

  • Khalil, R., Al Horani, M., Yousef, A., Sababheh, M.: A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  • Kumar, H., Chand, F: Dark and bright solitary wave solutions Of the higher order nonlinear Schröodinger equation with self-steepening and Self-frequency shift effects. J. Nonlinear Opt Phys. Mater. 22, 1–8 (2013)

    Article  Google Scholar 

  • Kumar, D., Darvishi, M.T., Joardar, A.K.: Modified Kudryashov method and its application to the fractional version of the variety of Boussinesq-like equations in shallow water. Opt. Quantum Electron. 50, 1–18 (2018)

    Article  Google Scholar 

  • Kumar, D., Seadawy, A.R., Joardar, A.K.: Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chinese Journal of Physics 56, 75–85 (2018)

    Article  ADS  Google Scholar 

  • Kurt, A., Tasbozan, O., Baleanu, D.: New solutions for conformable fractional Nizhnik-Novikov-Veselov system via \((\frac{G^{\prime }}{G})\)-expansion method and homotopy analysis method. Opt. Quantum Electron. 49, 1–10 (2017)

    Article  Google Scholar 

  • Lu, Dianchen, Seadawy, A.R., Arshad, M.: Bright-dark solitary wave and elliptic function solutions of unstable nonlinear Schr\({\ddot{o}}\)dinger equation and their applications. Opt. Quantum Electron 50, 23 (2018). https://doi.org/10.1007/s11082-017-1294-y

    Article  Google Scholar 

  • Pawlik, M., Rowlands, G.: The propagation of solitary waves in piezoelectric semiconductors. J. Phys. C 8, 1189–1204 (1975)

    Article  ADS  Google Scholar 

  • Pedlosky, V.E.: Finite-amplitude baroclinic waves. J. Atmos. Sci. 27, 15–30 (1970)

    Article  ADS  Google Scholar 

  • Seadawy, A.R.: Two-dimensional interaction of a shear flow with a free surface in a stratified fluid and its solitary-wave solutions via mathematical methods. Eur. Phys. J. Plus 132, 518 (2017). https://doi.org/10.1140/epjp/i2017-11755-6

    Article  Google Scholar 

  • Seadawy, A.R., El-Rashidy, K.: Traveling wave solutions for some coupled nonlinear evolution equations. Mathematical and Computer Modelling 57, 1371–1379 (2013)

    Article  MathSciNet  Google Scholar 

  • Wazwaz, A.M.: A study on linear and nonlinear Schrödinger equations by the variational iteration method. Chaos Solitons Fractals 37, 1136–1142 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Zhang, W.: Generalized variational principle for long water-wave equation by He’s semi-inverse method. Math. Probl. Eng. 2009, 1–6 (2009)

    ADS  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Razi University, Kermanshah, 67149, Iran

    M. T. Darvishi & M. Najafi

  2. Mathematics Department, Faculty of Science, Taibah University, Al-Madinah Al-Munawarah, Saudi Arabia

    Aly R. Seadawy

  3. Mathematics Department, Faculty of Science, Beni-Suef University, Beni Suef, Egypt

    Aly R. Seadawy

Authors
  1. M. T. Darvishi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Najafi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aly R. Seadawy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aly R. Seadawy.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Darvishi, M.T., Najafi, M. & Seadawy, A.R. Dispersive bright, dark and singular optical soliton solutions in conformable fractional optical fiber Schrödinger models and its applications. Opt Quant Electron 50, 181 (2018). https://doi.org/10.1007/s11082-018-1448-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-018-1448-6

Keywords

Search

Navigation