Skip to main content
SpringerLink
Log in

Improved wavelets based technique for nonlinear partial differential equations

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

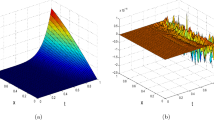
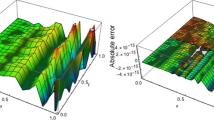
Abstract

One of the most challenging task now a days for engineers and scientists is finding solutions of nonlinear Partial Differential Equations (PDEs) which frequently arise in many engineering and physical phenomena’s. Encouraged by the ongoing research, a new technique is proposed in this article for obtaining more accurate results of nonlinear PDEs. Shifted Legendre wavelets and Picard’s Iteration Technique are used in the proposed technique. To test the significance of the proposed technique, nonlinear Gardner equation is considered and solved. The proposed technique provides very accurate results over a wider interval because of the use of the shifted polynomials. The results obtained are also compared with the results of Variational Iteration Method and the supremacy of the proposed method is established.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  • Ali, A., Iqbal, M.A., Mohyud-Din, S.T.: Chebyshev wavelets method for boundary value problems. Sci. Res. Essays 8(46), 2235–2241 (2013)

    Google Scholar 

  • Babolian, E., Zadeh, F.F.: Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration. Appl. Math. Comput. 188, 417–426 (2007)

    MathSciNet  MATH  Google Scholar 

  • Bekir, A., Aksoy, E., Guner, O.: Optical soliton solutions of the long-short-wave interaction system. J. Nonlinear Optic. Phys. Mater. 22(2), 1350015 (2013)

    Article  ADS  Google Scholar 

  • Bekir, A., Guner, O., Bilgil, H.: Optical soliton solutions for the variable coefficient modified Kawahara equation. Opt. Int J. Light Electron Opt. 126(20), 2518–2522 (2015). doi:10.1016/j.ijleo.2015.06.051

    Article  Google Scholar 

  • Cattani, C., Kudreyko, A.: Harmonic wavelet method towards solution of the Fredholm type integral equations of the second kind. Appl. Math. Comput. 215, 4164–4171 (2010)

    MathSciNet  MATH  Google Scholar 

  • Guner, O., Bekir, A.: Optical solitons for nonlinear coupled Klein-Gordon equations. Optoelectron. Adv. Mater. Rap. Commun. 9(3–4), 332–343 (2015)

    Google Scholar 

  • Guner, O., Bekir, A.: Bright and dark soliton solutions for some nonlinear fractional differential equations. Chin. Phys. B 25(3), 30203 (2016). doi:10.1088/1674-1056/25/3/030203

    Article  Google Scholar 

  • Islam, S., Zuhra, S., Idrees, M., Ullah, H., Shah, I.A., Zaman, A.: Application of Optimal Homotopy Asymptotic Method to Benjamin-Bona-Mahony and Sawada-Kotera Equations. World Appl. Sci. J. 31(11), 1945–1951 (2014)

    Google Scholar 

  • Mohammadi, F., Hosseini, M.M., Mohyud-din, S.T.: Legendre wavelet Galerkin method for solving ordinary differential equations with non analytical solution. Int. J. Syst. Sci. 42(4), 579–585 (2011)

    Article  MATH  Google Scholar 

  • Noor, M.A., Mohyud-Din, S.T.: Variational iteration method for solving higher-order nonlinear boundary value problems using He’s polynomials. Int. J. Nonlinear Sci. Numer Simul. 9(2), 141–157 (2008)

    Article  MATH  Google Scholar 

  • Saeed, U., Rehman, M., Iqbal, M.A.: Haar Wavelet-Picard technique for fractional order nonlinear initial and boundary value problems. Sci. Res. Essays 9(12), 571–580 (2014)

    Article  Google Scholar 

  • Wazwaz, A.M.: Approximate solutions to boundary value problems of higher order by the modified decomposition method. Comput. Math Appl. 40, 679–691 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  • Wazwaz, A.M.: Partial Differential Equations and Solitary Waves Theory. Springer, Nonlinear physical science (2009)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

The authors are highly grateful to the unknown referees for their valuable comments.

Author information

Authors and Affiliations

  1. Department of Mathematics, MohiUd Din Islamic University, Nerian Sharif, AJ&K, Pakistan

    Muhammad Asad Iqbal & Muhammad Shakeel

  2. Department of Mathematics, Institute of Southern Punjab, Multan Campus, Multan, Pakistan

    Ayyaz Ali

  3. Department of Mathematics, Faculty of Sciences, HITEC University, Taxila, Pakistan

    Syed Tauseef Mohyud-Din

Authors
  1. Muhammad Asad Iqbal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Shakeel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ayyaz Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Syed Tauseef Mohyud-Din
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Syed Tauseef Mohyud-Din.

Ethics declarations

Conflict of interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Iqbal, M.A., Shakeel, M., Ali, A. et al. Improved wavelets based technique for nonlinear partial differential equations. Opt Quant Electron 49, 167 (2017). https://doi.org/10.1007/s11082-017-1001-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-017-1001-z

Keywords

Search

Navigation