Skip to main content
SpringerLink
Log in

Theoretical conversion of the hypergeometric-Gaussian beams family into a high-order spiraling Bessel beams by a curved fork-shaped hologram

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

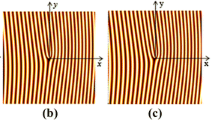
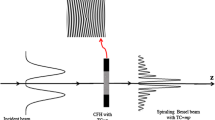
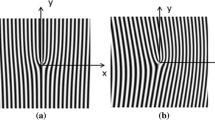
Based on the process of the Fresnel diffraction, the possibility of generating a new type of laser beams family by illuminating a curved fork-shaped hologram, with an input hypergeometric-Gaussian beams family of orders n and m is studied in this paper. The theoretical and the numerical results showed that, at the output plane, a high order spiraling Bessel vortex beam is produced. This vortex beam is divergence or non-divergence depending upon the waist position of the input hypergeometric-Gaussian beams, regarding the plane where the curved fork-shaped hologram is situated. Analytical expressions of the amplitude and the intensity distribution of the diffracted wave field are calculated and deduced using the stationary phase method. The actual work generalizes also the Fresnel diffraction study of some subfamilies of the hypergeometric-Gaussian beams family, such as: fundamental Gaussian, hollow Gaussian, modified quadratic Bessel–Gaussian and elegant Laguerre–Gaussian beams.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  • Arlt, J., Garcez-Chavez, V., Sibbett, W., Dholakia, K.: Optical micromanipulation using Bessel light beam. Opt. Commun. 197, 239–245 (2001)

    Article  ADS  Google Scholar 

  • Bazhenov, V.Y., Vasnetsov, M.V., Soskin, M.S.: Laser beams with screw dislocation in their wavefronts. Pis’ma Zh. Eksp. Teor. Fiz 52, 1037–1039 (1990)

    ADS  Google Scholar 

  • Beijersbergen, M.W., Coerwinkel, R.P.C., Kristensen, M., Woerdman, J.P.: Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 112, 321–327 (1994)

    Article  ADS  Google Scholar 

  • Bekshaev, A., Orlinska, O., Vasnetsov, M.: Optical vortex generation with a “fork” hologram under conditions of high-angle diffraction. Opt. Commun. 283, 2006–2016 (2010)

    Article  ADS  Google Scholar 

  • Berry, M.V.: Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A: Pure Appl. Opt. 6, 259–268 (2004)

    Article  ADS  Google Scholar 

  • Buchholz, H.: The Confluent Hypergeometric Function with Special Emphasis on its Applications. Springer, New York (1969)

    Book  MATH  Google Scholar 

  • Carpentier, A.V., Michinel, H., Salgueiro, J.R., Olivieri, D.: Making optical vortices with computer-generated holograms. Am. J. Phys. 76, 916–921 (2008)

    Article  ADS  Google Scholar 

  • Chen, J., Wang, G., Xu, Q.: Production of confluent hypergeometric beam by computer-generated hologram. Opt. Eng. 50, 024201–024205 (2011)

    Article  ADS  Google Scholar 

  • Ebrahim, A.A.A., Khannous, F., Chafiq, A., Belafhal, A.: Theoretical investigation of propagation characteristics of hypergeometric-Gaussian beams type-II through an ABCD optical system with an annular aperture. Int. J. Photonics Opt. Technol. 2, 18–24 (2016)

    Google Scholar 

  • Ebrahim, A.A.A., Khannous, F., Nebdi, H., Chafiq, A., Belafhal, A.: Generalized M2-factor of hard-edged diffracted hypergeometric-Gaussian type-II beams. Phys. Chem. News 73, 50–57 (2014)

    Google Scholar 

  • Erdelyi, A., Magnus, W., Oberhettinger, F.: Tables of Integral Transforms. McGraw-Hill, New York (1954)

    MATH  Google Scholar 

  • Ez-zariy, L., Belafhal, A.: The conversion of a Li’s flat-topped-Gaussian beam to a superposition of Kummer dark hollow beam by the illumination of a fractional radial Hilbert transform system. Opt. Quantum Electron. 48, 331–344 (2016)

    Article  Google Scholar 

  • Ez-zariy, L., Khannous, F., Nebdi, H., Khouilid, M., Belafhal, A.: Generation of new doughnut beams from Li’s flattened Gaussian beams. J. Optoelectron. Adv. Mater. 15, 1188–1199 (2013)

    Google Scholar 

  • Ge, S.Q., Ya, Z.K., Yu, F.G., Jun, L.Z., Tian, L.S.: Generalization and propagation of spiraling Bessel beams with a helical axicon. Chin. Phys. B 21, 014208–014218 (2012)

    Article  ADS  Google Scholar 

  • Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series and Products, 7th edn. Elsevier, Amsterdam (2007)

    MATH  Google Scholar 

  • He, H., Heckenberg, N.R., Rubinsztein-Dunlop, H.: Optical particle trapping with higher-order doughnut beams produced using high efficiency computer generated holograms. J. Mod. Opt. 42, 217–223 (1995)

    Article  ADS  Google Scholar 

  • Heckenberg, N.R., Mcduff, R., Smith, C.P., Rubinsztein-Dunlop, H., Wegener, M.J.: Laser beams with phase singularities. Opt. Quantum Electron. 24, S951–S962 (1992)

    Article  Google Scholar 

  • Janicijevic, L., Topuzoski, S.: Fresnel and Fraunhofer diffraction of a Gaussian laser beam by fork-shaped gratings. J. Opt. Soc. Am. A 25, 2659–2669 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Jarutis, V., Matijošius, A., Trapani, P.D., Piskarskas, A.: Spiraling zero-order Bessel beam. Opt. Lett. 34, 2129–2131 (2009)

    Article  ADS  Google Scholar 

  • Karimi, E., Zito, G., Piccirillo, B., Marrucci, L., Santamato, E.: Hypergeometric-Gaussian modes. Opt. Lett. 21, 3053–3055 (2007a)

    Article  ADS  Google Scholar 

  • Karimi, E., Piccirillo, B., Marrucci, L., Santamato, E.: Improved focusing with hypergeometric-Gaussian type-II optical modes. Opt. Express. 16, 21069–21075 (2007b)

    Article  ADS  Google Scholar 

  • Khannous, F., Ebrahim, A.A.A., Belafhal, A.: A closed form of kurtosis parameter of hypergeometric-Gaussian type-II beam. Chin. Phys. B 25, 044206–044213 (2016)

    Article  Google Scholar 

  • Khonina, S.N., Kotlyar, V.V., Shinkaryev, M.V., Soifer, V.A., Uspleniev, G.V.: The phase rotor filter. J. Mod. Opt. 39, 1147–1154 (1992a)

    Article  ADS  Google Scholar 

  • Khonina, S.N., Kotlyar, V.V., Soifer, V.A., Shinkaryev, M.V., Uspleniev, G.V.: Trochoson. Opt. Commun. 91, 158–162 (1992b)

    Article  ADS  Google Scholar 

  • Kotlyar, V.V., Kovalev, A.A., Nalimov, A.G.: Propagation of hypergeometric laser beams in a medium with a parabolic refractive index. J. Opt. 15, 125706–125716 (2013)

    Article  ADS  Google Scholar 

  • Kotlyar, V.V., Kovalev, A.A., Soifer, V.A., Tuvey, C.S., Davis, J.A.: Sidelobe contrast reduction for optical vortex beams using a helical axicon. Opt. Lett. 32, 921–923 (2007)

    Article  ADS  Google Scholar 

  • Lee, W.M., Yuan, X.-C., Cheong, W.C.: Optical vortex beam shaping by use of highly efficient irregular spiral phase plates for optical micromanipulation. Opt. Lett. 29, 1796–1798 (2004)

    Article  ADS  Google Scholar 

  • Li, J., Chen, Y.: Propagation of confluent hypergeometric beam through uniaxial crystals orthogonal to the optical axis. Opt. Laser Technol. 44, 1603–1610 (2012)

    Article  ADS  Google Scholar 

  • Luo, D., Kuang, C., Hao, X., Liu, X.: High-precision laser alignment technique based on spiral phase plate. Opt. Lasers Eng. 50, 944–949 (2012)

    Article  Google Scholar 

  • Machavariani, G., Davidson, N., Hasman, E., Blit, S., Ishaaya, A.A., Friesem, A.A.: Efficient conversion of a Gaussian beam to a high purity helical beam. Opt. Commun. 209, 265–271 (2002)

    Article  ADS  Google Scholar 

  • Mair, A., Vaziri, A., Weihs, G., Zeilinger, A.: Entanglement of the orbital angular momentum states of photons. Nature. 412, 313–316 (2001)

    Article  ADS  Google Scholar 

  • Massari, M., Ruffato, G., Gintoli, M., Ricci, F., Romanato, F.: Fabrication and characterization of high-quality spiral phase plates for optical applications. Appl. Opt. 54, 4077–4083 (2015)

    Article  ADS  Google Scholar 

  • McGloin, D., Dholakia, K.: Bessel beams: diffraction in a new light. Contemp. Phys. 46, 15–28 (2005)

    Article  ADS  Google Scholar 

  • Paterson, C., Smith, R.: Higher-order Bessel waves produced by axicon-type computer-generated holograms. Opt. Commun. 124, 121–130 (1996)

    Article  ADS  Google Scholar 

  • Qu, J., Fang, M., Peng, J., Huang, W.: The fractional Fourier transform of hypergeometric-Gauss beams through the hard edge aperture. Prog. Electromagn. Res. M 43, 31–38 (2015)

    Article  Google Scholar 

  • Saad, F., El Halba, E.M., Belafhal, A.: Generation of generalized spiraling Bessel beams of arbitrary order by curved fork-shaped holograms. Opt. Quantum Electron. 48, 454–466 (2016)

    Article  Google Scholar 

  • Stoyanov, L., Topuzoski, S., Stefanov, I., Janicijevic, L., Dreischuh, A.: Far field diffraction of an optical vortex beam by a fork-shaped grating. Opt. Commun. 350, 301–308 (2015)

    Article  ADS  Google Scholar 

  • Tang, B., Jiang, C., Zhu, H.: Fractional Fourier transform for confluent hypergeometric beams. Phys. Lett. A 376, 2627–2631 (2012)

    Article  ADS  Google Scholar 

  • Topuzoski, S.: Fraunhofer diffraction of Laguerre–Gaussian laser beam by helical axicon. Opt. Commun. 330, 184–190 (2014)

    Article  ADS  Google Scholar 

  • Topuzoski, S.: Generation of optical vortices with curved fork-shaped hologram. Opt. Quantum Electron. 48, 138–144 (2016)

    Article  Google Scholar 

  • Topuzoski, S., Janicijevi, L.: Conversion of high-order Laguerre–Gaussian beams into Bessel beams of increased, reduced or zeroth order by use of a helical axicon. Opt. Commun. 282, 3426–3432 (2009)

    Article  ADS  Google Scholar 

  • Vasara, A., Turunen, J., Friberg, A.T.: Realization of general nondiffracting beams with computer-generated holograms. J. Opt. Soc. Am. A 6, 1748–1754 (1989)

    Article  ADS  Google Scholar 

  • Xia, Y., Yin, J.: Generation of a focused hollow beam by an 2π-phase plate and its application in atom or molecule optics. J. Opt. Soc. Am. B 22, 529–536 (2005)

    Article  ADS  Google Scholar 

  • Xie, Q., Zhao, D.: Optical vortices generated by multi-level achromatic spiral phase plates for broadband beams. Opt. Commun. 281, 7–11 (2008)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The first and second authors were supported by the Ministry of higher Education and Scientific Research and the Ministry of Education of Yemen.

Author information

Authors and Affiliations

  1. Laboratory of Nuclear, Atomic and Molecular Physics, Department of Physics, Faculty of Sciences, Chouaïb Doukkali University, P. B 20, 24000, El Jadida, Morocco

    A. A. A. Ebrahim, F. Saad, L. Ez-zariy & A. Belafhal

Authors
  1. A. A. A. Ebrahim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Saad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. Ez-zariy
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. Belafhal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Belafhal.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahim, A.A.A., Saad, F., Ez-zariy, L. et al. Theoretical conversion of the hypergeometric-Gaussian beams family into a high-order spiraling Bessel beams by a curved fork-shaped hologram. Opt Quant Electron 49, 169 (2017). https://doi.org/10.1007/s11082-017-0987-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-017-0987-6

Keywords

Search

Navigation