Abstract
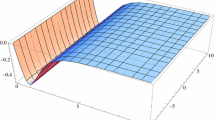
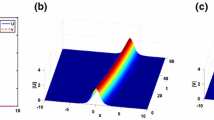
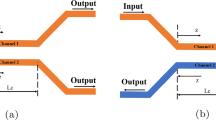
We present an extensive numerical investigation on the interaction dynamics of optical bright solitons in asymmetric nonlinear directional couplers taking into account the effects of group velocity mismatch, phase-velocity mismatch and differences in group velocity dispersions and effective mode areas between two cores. We also numerically explore the stability of bright solitons in the presence of harmonic infinitesimal perturbation, which is seeded in the form of uniform white noise. To have a comprehensive picture, we finally emphasize the influence of every individual asymmetric parameters on the soliton interaction in asymmetric nonlinear directional couplers.










Similar content being viewed by others
References
Agrawal, G.: Applications of Nonlinear Fiber Optics. Academic Press, London (2001)
Agrawal, G.P.: Nonlinear Fiber Optics. Academic Press, London (2007)
Atai, J., Malomed, B.A., Merhasin, I.M.: Stability and collisions of gap solitons in a model of a hollow optical fiber. Opt. Commun. 265(1), 342–348 (2006)
Atai, J., Malomed, B.A.: Stability and interactions of solitons in two-component active systems. Phys. Rev. E 54, 4371–4374 (1996)
Atai, J., Malomed, B.A.: Stability and interactions of solitons in asymmetric dual-core optical waveguides. Opt. Commun. 221(3), 55–62 (2003)
Biswas, A.: Soliton–soliton interaction in optical fibers. J. Nonlinear Opt. Phys. Mater. 8(04), 483–495 (1999)
Blow, K.J., Doran, N.J.: Bandwidth limits of nonlinear (soliton) optical communication systems. Electron. Lett. 19(11), 429–430 (1983)
Chu, P.L., Desem, C.: Gaussian pulse propagation in nonlinear optical fibre. Electron. Lett. 19(23), 956–957 (1983)
Chu, P.L., Desem, C.: Effect of third-order dispersion of optical fibre on soliton interaction. Electron. Lett. 21(6), 228–229 (1985)
Cohen, G.: Soliton interaction and stability in nonlinear directional fiber couplers. Phys. Rev. E 52(5), 5565–5573 (1995)
Cuevas-Maraver, J., Kevrekidis, P., Williams, F.: The Sine-Gordon Model and Its Applications: From Pendula and Josephson Junctions to Gravity and High-Energy Physics. Springer, New York (2014)
Gordon, J.P.: Interaction forces among solitons in optical fibers. Opt. Lett. 8(11), 596–598 (1983)
Govindaraji, A., Mahalingam, A., Uthayakumar, A.: Dark soliton switching in nonlinear fiber couplers with gain. Opt. Laser Technol. 60, 18–21 (2014)
Govindaraji, A., Mahalingam, A., Uthayakumar, A.: Numerical investigation of dark soliton switching in asymmetric nonlinear fiber couplers. Appl. Phys. B 120(2), 341–348 (2015)
He, X., Xie, K., Xiang, A.: Optical solitons switching in asymmetric dual-core nonlinear fiber couplers. Optik - Int. J. Light Electron Opt. 122(14), 1222–1224 (2011)
Jensen, S.: The nonlinear coherent coupler. IEEE J. Quantum. Electron. 18(10), 1580–1583 (1982)
Kanna, T., Lakshmanan, M.: Exact soliton solutions, shape changing collisions, and partially coherent solitons in coupled nonlinear schrödinger equations. Phys. Rev. Lett. 86(22), 5043–5046 (2001)
Kanna, T., Lakshmanan, M., Tchofo Dinda, P., Akhmediev, N.: Soliton collisions with shape change by intensity redistribution in mixed coupled nonlinear schrödinger equations. Phys. Rev. E 73(2), 026604 (2006)
Kaup, D.J., Malomed, B.A.: Gap solitons in asymmetric dual-core nonlinear optical fibers. J. Opt. Soc. Am. B 15(12), 2838–2846 (1998)
Li, Q., Zhang, A., Hua, X.: Numerical simulation of solitons switching and propagating in asymmetric directional couplers. Opt. Commun. 285(2), 118–123 (2012)
Mak, W.C.K., Malomed, B.A., Chu, P.L.: Solitons in coupled waveguides with quadratic nonlinearity. Phys. Rev. E 55(5), 6134–6140 (1997)
Mitschke, F.M., Mollenauer, L.F.: Experimental observation of interaction forces between solitons in optical fibers. Opt. Lett. 12(5), 355–357 (1987)
Nóbrega, K.Z., da Silva, M.G., Sombra, A.S.B.: Multistable all-optical switching behavior of the asymmetric nonlinear directional coupler. Opt. Commun. 173(16), 413–421 (2000)
Radhakrishnan, R., Lakshmanan, M., Hietarinta, J.: Inelastic collision and switching of coupled bright solitons in optical fibers. Phys. Rev. E 56(2), 2213–2216 (1997)
Shum, P., Liu, M.: Effects of intermodal dispersion on two-nonidentical-core coupler with different radii. Photon. Technol. Lett. IEEE 14(8), 1106–1108 (2002)
Smith, K., Mollenauer, L.F.: Experimental observation of soliton interaction over long fiber paths: discovery of a long-range interaction. Opt. Lett. 14(22), 1284–1286 (1989)
Tsang, S.C., Chiang, K.S., Chow, K.W.: Soliton interaction in a two-core optical fiber. Opt. Commun. 229(1), 431–439 (2004)
Vijayajayanthi, M., Kanna, T., Lakshmanan, M.: Bright-dark solitons and their collisions in mixed n-coupled nonlinear schrödinger equations. Phys. Rev. A 77(1), 013820 (2008)
Yang, C.C.: All-optical ultrafast logic gates that use asymmetric nonlinear directional couplers. Opt. Lett. 16(21), 1641–1643 (1991)
Yang, C.-C., Wang, A.J.S.: Asymmetric nonlinear coupling and its applications to logic functions. Quantum Electron. IEEE J. 28(2), 479–487 (1992)
Acknowledgements
One of us (AG) is indebted to Professor M. Lakshmanan for his fruitful discussions and valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Govindaraji, A., Mahalingam, A. & Uthayakumar, A. Interaction dynamics of bright solitons in linearly coupled asymmetric systems. Opt Quant Electron 48, 563 (2016). https://doi.org/10.1007/s11082-016-0844-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-016-0844-z