Abstract
We investigated the focusing properties of a cylindrically polarized annular multi Gaussian beam tightly focused with a high NA lens and a complex phase filter. It is observed that a properly designed complex phase filter can generate multiple focal spot and focal hole segments along optical axis its useful for the manipulation of multiple optical traps of low and high refractive index particles.
Similar content being viewed by others
1 Introduction
Recently, there is an increasing interest in the spatially inhomogeneous polarization, mostly driven by the advances made in micro-fabrication techniques and theoretical modeling techniques that were not available homogeneous polarization. One example of such spatially inhomogeneous polarization that has attracted much of the interest is the so-called cylindrical vector (CV) beams. Cylindrical vector beams are solutions of Maxwell equations that obey cylindrical symmetry both in amplitude and polarization. Cylindrical vector beams can be divided into radially polarization, azimuthal polarization and generalized cylindrical polarization, according to the actual polarization pattern. One can use two cascaded half-wave plates to conveniently convert a radially polarization or azimuthal polarization into a generalized cylindrical vector beam, or vice versa (Zhan and Leger 2002; Friedman et al. 2002). Growing interest in the generation of three-dimensional (3D) optical beams that are dark regions in space surrounded by light are driven by wide ranging applications including dark optical traps for atoms (Zhan and Leger 2002; Friedman et al. 2002), manipulation, guiding and binding of microparticles and biological cells (Cizmar et al. 2010), erase beams for super-resolution fluorescence microscopy (Watanabe et al. 2003), etc. Over the past years, a variety of techniques have been proposed for generating such optical bottle beams for applications in optical tweezers and atom traps (Garcia-Sucerquia et al. 2004; Chen and Zhan 2006; Bokor and Davidson 2006; Ahluwalia et al. 2006; Arlt and Padgett 2000; Ahluwalia et al. 2004; Yelin et al. 2004; Pu et al. 2005). However, stable trapping of a single particle is expected if we can make the bottles small enough and comparable to the particle size. Such “microbottles” were established recently with the volume speckle field (Isenhower et al. 2009). Recently particle trapping experiment is successfully done by Ashkin et al. (1986), particles manipulations have drawn great interests. For example, owning to the abilities to manipulate and isolate microscopic objects in a precise and nondestructive manner, optical tweezers are widely used in micromachines and microscopy (Unger and Marston 1988; Crocker and Grier 1994; Wright et al. 1990; Tadir et al. 1989). In order to improve the speed of particle trapping, the optical tweezers with multitraps are ideal (Huang et al. 2011; Guo et al. 2011). In 2002, two dimensional arrays of focal spots are formed by multi beam systems (Eriksen et al. 2002). However, it is just for two dimensional particles trapping. In 2005, Casaburi et al. (2005) achieve multi-3D-optical trapping by utilizing two- and three-beam interference, which, in order to ensure destructive interference at the focus, require extremely high interferometric precision among the three beams. Recently several methods to generate the multiple optical trapping have been suggested (Prabakaran et al. 2014a, b; Zhao et al. 2005; Cao et al. 2013; Jian-Nong et al. 2011; Charles et al. 2014). In this paper, we wish to analyze the focusing property of the phase modulated cylindrically polarized annular multi Gaussian beam (CVAMB) tightly focused with high NA lens.
2 Principle of the optical focusing system
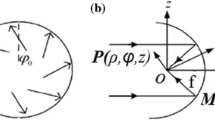
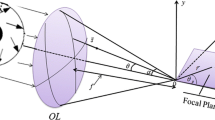
A schematic diagram of the suggested method is shown in Fig. 1. The cylindrically polarized annular multi Gaussian beam is focused through a high NA lens system focused. The annular multi-Gaussian beams consist of a small sum of finite-width annular Gaussian beams side by side each of which represents an intuitive component of the entire beam. The analysis was performed on the basis of Richards and Wolf’s vectorial diffraction method (Richards and Wolf 1959) widely used for high-NA lens system at arbitrary incident polarization. In the case of the incident polarization, adopting the cylindrical coordinates r, z, φ and the notations of Youngworth and Brown (2000), the focal field of a cylindrically polarized vortex beam can be written as:
where E r , E z , E φ are the amplitudes of the three orthogonal components and \(\vec{e}_{r}\), \(\vec{e}_{z}\), \(\vec{e}_{\varphi }\) are their corresponding unit vectors. The three orthogonal components of the electric field is given as:
where, k = 2π/λ is the wave number and Jn(x) is the Bessel function of the first kind with order n. r and z are the radial and z coordinates of observation point in focal region, respectively P(θ) describes the amplitude-modulated annular multi-Gaussian beam, this function is given by Jian-Nong et al. (2011)
here, θ is the converging semi-angle. We denote the maximum converging semi-angle as θmax which is related to objective numerical aperture by θmax = arcsin(NA). θ0 is an angle which, along with integer m, determines the shape of the modulation function. θ0 is usually chosen to be slightly smaller than θmax. θc determines the radial position translation of the P(θ). Here we take θc = θmax/2. w0 is the waist width of single Gaussian beam which is calculated by the following formula:
Equation (5) describes an object beam. The factor (θ/θ0) measures that the most of light energy is located on the annular edge of the pupil. Increasing the integer m will concentrate more energy into the annular edge area in which the converging semi-angle is more than θ0. The sum of (2N + 1) spatially equally spaced Gaussian beams ensures that the amplitude of the constructed annular multi-Gaussian beam decreases suddenly when reaching the outer edge of the pupil. Such an amplitude modulated beam can be realized by encoding suitable phase mask on spatial light modulator. The effect complex filter on the input radially polarized beam is evaluated by replacing the function P(θ) by P(θ) CPF(θ). Where CPF(θ) is given by:
Basing on the above equations, focusing properties of cylindrically polarized annular multi Gaussian beam (CPAMGB) with complex phase plate can be investigated theoretically.
3 Results and discussion
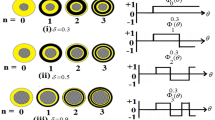
We perform the integration of Eq. (1) numerically for NA = 0.9 and λ = 1, θmax = 64.19°, θ0 = 60° and θc = α/2, w0 = 0.02710, N = 20 and m = 4. Here, for simplicity, we assume that the refractive index n = 1 and A = 1. For all calculation in the length unit is normalized to λ and the energy density is normalized to unity. The intensity distribution for ϕ = 0º, which corresponds to a radially polarized annular multi Gaussian incident beam for the high NA lens is Shown in Fig. 2a, b. It is observed from the figure, that it is possible to generate a series of eight focal spot each having FWHM of 0.66λ and are axially separated by the distance of 2λ between them. The set of angles of complex phase filter (CPF) optimized for the above mentioned focal segment using traditional Global Search Algorithm are θ1 = 42.47°, θ2 = 45.33°, θ3 = 61.91°, θmax = 64.19°. However, It is observed from Fig. 2c, d, while setting ϕ = 90°, which corresponds to a azimuthally polarized annular multi Gaussian beam, the above motioned CPF generates a series of eight focal holes each having FWHM of 0.5λ and are axially separated by the distance of 2λ between them. The on axial intensity distribution at r = 0.3λ is found to be almost uniform in the vicinity of focus and is shown in Fig. 2c. The Fig. 3a, b shows the focal segment generated for ϕ = 0°, for the CPF optimized with angles θ1 = 26.75°, θ2 = 52.93°, θ3 = 58.78°, θmax = 64.19°. We observed from the figure, that the single focal spot is splitted into two focal spot each having FWHM of 0.74λ and are axially separated by a distance of 2λ. The DOF of the each focal spot is measured as 2.8λ. We also observed that the same CPF generated two focal hole each having FWHM of 0.8λ and are separated by axial distance of 2.5λ between them for the polarization angle ϕ = 90°. The DOF of the each focal hole is measured as 2.8λ and is shown in Fig. 3c, d. The Fig. 4a, b shows that by setting the three angles of CPF as θ1 = 42.47°, θ2 = 49.93°, θ3 = 61.91°, θmax = 64.19°. We can generate a series of four focal spots each having FWHM of 0.6λ and are axially separated by the distance of 2λ between them for the polarization angle ϕ = 0°. However, from the Fig. 4c, d, we observed that by setting the polarization angle ϕ = 90°, the same CPF generates a series of four focal holes each having FWHM of 0.8λ and are axially separated by a distance of 2λ. Thus by using the above optimized CPF and by tuning the polarization angle of the incident cylindrically polarized annular multi Gaussian beam (CPAMGB) from ϕ = 0° to ϕ = 90°, it is possible to generate a series of four focal spot and focal hole respectively. The Fig. 5a, b shows the focal segment generated for ϕ = 0°, for the CPF optimized with angles θ1 = 42.47°, θ2 = 46.86°, θ3 = 61.91°, θmax = 64.19°. We observed from the figure, it is possible to generated series of six focal spot each having FWHM of 0.65λ and are axially separated by a distance of 3.8λ. The DOF of the each focal spot is measured as 2λ. We also observed that the same CPF generated thirteen sub wavelength focal hole each having FWHM of 0.5λ and are separated by axial distance of 2 λ between them for the polarization angle ϕ = 90°. The DOF of the each focal hole is measured as 2.3λ is shown in Fig. 5b, d respectively. The above simulation calculations show that, by utilizing the CPF to modulate the phase of CPAMGB, the optical spot in the focal region can be used as a powerful tool for particle manipulation. Here, each particle in the focal spot and focal hole is three dimensionally trapped separately with a small space along z axis. In addition, multi focal spots can be able to trap multi particles synchronously. It’s simple and flexible method of forming multiple focal spot and focal hole with sub wavelength size introduced in this paper. This type of beam profile is useful in particle manipulation and optical trapping for high refractive index and low refractive index particles can be achieved precisely and controllably.
4 Conclusion
In conclusion, a novel method for demonstrated the effect of phase modulation on the intensity distribution on tight focusing of cylindrically polarized annular multi Gaussian beam in the focal region of high NA lens using Vector diffraction theory. We presented possible design of complex phase filter to achieve multiple focal spot and focal hole segments which finds wide applications in optical tweezers, micromanipulation of high and low refractive index particles, microscopy, and optical storage.
References
Ahluwalia, B.P.S., Yuan, X.C., Tao, S.H.: Transfer of pure on-axis spin angular momentum to the absorptive particle using self-imaged bottle beam optical tweezers system. Opt. Express 12, 5172–5177 (2004)
Ahluwalia, B.P.S., Cheong, W.C., Yuan, X.C.: Design and fabrication of a double-axicon for generation of tailorable self-imaged three-dimensional intensity voids. Opt. Lett. 31, 987–989 (2006)
Arlt, J., Padgett, M.J.: Generation of a beam with a dark focus surrounded by regions of higher intensity: the optical bottle beam. Opt. Lett. 25, 191–193 (2000)
Ashkin, A., Dziedzic, J.M., Bjorkholm, J.E., Chu, S.: Observation of a single-beam Gradient force optical trap for dielectric particles. Opt. Lett. 11, 288–290 (1986)
Bokor, N., Davidson, N.: Generation of a hollow dark spherical spot by 4pi focusing of a radially polarized Laguerre–Gaussian beam. Opt. Lett. 31, 149–151 (2006)
Cao, J., Chen, Q., Guo, H.: Creation of a controllable three dimensional optical chain by TEM01 mode radially polarized Laguerre–Gaussian beam. Optik 124, 2033–2036 (2013)
Casaburi, A., Pesce, G., Zemánek, P.: Two- and three-beam interferometric optical tweezers. Opt. Commun. 251, 393–404 (2005)
Charles, J.W., Prabakaran, K., Rajesh, K.B., Pandya, H.M., Musthafa, A.M.: Generation of sub wavelength multiple focal hole segments using azimuthally polarized annular multi-Gaussian beam. Optik 125, 3328–3330 (2014)
Chen, W., Zhan, Q.: Three-dimensional focus shaping with cylindrical vector beams. Opt. Commun. 265, 411–417 (2006)
Cizmar, T., Romero, L.C.D., Dholakia, K., Andrews, D.L.: Multiple optical trapping and binding: new routes to self-assembly. J. Phys. B 43, 102001 (2010)
Crocker, J.C., Grier, D.: Microscopic measurement of the pair interaction potential of charge-stabilized colloid. Phys. Rev. Lett. 73, 352–355 (1994)
Eriksen, R.L., Mogensen, P.C., Glückstad, J.: Multiple-beam optical tweezers generated by the generalized phase-contrast method. Opt. Lett. 27, 267–269 (2002)
Friedman, N., Kaplan, A., Davidson, N.: Dark optical traps for cold atoms. Adv. At. Mol. Opt. Phys. 48, 99–151 (2002)
Garcia-Sucerquia, J., Medina, F.F., Matteucci, G.: Optical tubular structures produced by diffraction of circular apertures. Opt. Lasers Eng. 42, 61–70 (2004)
Guo, H., Dong, X., Weng, X., Sui, G., Yang, N., Zhuang, S.: Multifocus with small size, uniform intensity, and nearly circular symmetry. Opt. Lett. 36, 2200–2202 (2011)
Huang, K., Shi, P., Cao, G.W., Li, K., Zhang, X.B., Li, Y.P.: Vector-vortex Bessel–Gauss beams and their tightly focusing properties. Opt. Lett. 36, 888–890 (2011)
Isenhower, L., Williams, W., Dally, A., Saffman, M.: Atom trapping in an interferometrically generated bottle beam trap. Opt. Lett. 34, 1159–1161 (2009)
Jian-Nong, C., Qin-Feng, X., Gang, X.: Tight focus of a radially polarized and amplitude-modulated annular multi-Gaussian beam. Chin. Phys. B 20, 114211–114215 (2011)
Prabakaran, K., Rajesh, K.B., Pillai, T.V.S., Chandrasekaran, R., Jaroszewicz, Z.: Generation of multiple focal spot and focal hole of sub wavelength scale using phase modulated LG (1,1) beam. Optik 124, 5086–5088 (2014a)
Prabakaran, K., Rajesh, K.B., Anbarasan, P.M.: Tight focusing of phase modulated radially polarized hollow Gaussian beam using complex phase filter. Optik 125, 6965–6968 (2014b)
Pu, J.X., Liu, X.Y., Nemoto, S.: Partially coherent bottle beams. Opt. Commun. 252, 7–11 (2005)
Richards, B., Wolf, E.: Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. A Math. Phys. Sci. 253(1274), 358–379 (1959)
Tadir, Y., Wright, W.H., Vafa, O., Ord, T., Asch, R.H., Berns, M.W.: Micromanipulation of sperm by a laser generated optical trap. Fertil. Steril. 52, 870–873 (1989)
Unger, B.T., Marston, P.L.: Optical levitation of bubbles in water by the radiation pressure of a laser beam: an acoustically quiet levitator. J. Acoust. Soc. Am. 83, 970–975 (1988)
Watanabe, T., Iketaki, Y., Omatsu, T., Yamamoto, K., Sakai, M., Fuji, M.: Two point separation in super-resolution fluorescence microscope based on up-conversion fluorescence depletion technique. Opt. Express 11, 3271–3276 (2003)
Wright, W.H., Sonek, G., Tadir, Y., Berns, M.W.: Laser trapping in cell biology. IEEE J. Quantum Electron. 26, 2148–2157 (1990)
Yelin, D., Bouma, B.E., Tearney, G.J.: Generating an adjustable three-dimensional dark focus. Opt. Lett. 29, 661–663 (2004)
Youngworth, K.S., Brown, T.G.: Focusing of high numerical aperture cylindrical vector beams. Opt. Express 7, 77–87 (2000)
Zhan, Q., Leger, J.R.: Focus shaping using cylindrical vector beams. Opt. Express 10, 324–331 (2002)
Zhao, Y., Zhan, Q., Zhang, Y., Li, Y.P.: Creation of a three dimensional optical chain for controllable particle delivery. Opt. Lett. 30, 848–850 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chandrasekaran, R., Prabakaran, K. & Rajesh, K.B. Generation of multiple focal spot and focal hole segments using phase modulated cylindrically polarized annular multi-Gaussian beam. Opt Quant Electron 48, 39 (2016). https://doi.org/10.1007/s11082-015-0311-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-015-0311-2