Abstract
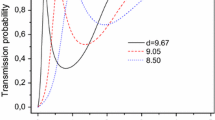
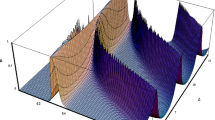
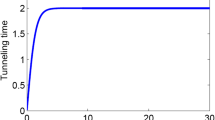
General expressions of tunneling probability for arbitrarily graded potential barriers are rigorously derived using the modified Airy functions. Three types of graded potential barriers for which exact solutions exist are taken as examples for comparison’s purpose. Results obtained by the proposed method are confirmed to be in fairly good agreement with exact ones, demonstrating the usefulness of the modified Airy functions method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Abramowitz M., Stegun I.A.: Handbook of mathematical functions, pp. 446. Dover Publication, New York (1970)
Ando Y., Itoh T.: Calculation of transmission tunneling current across arbitrary potential barriers. J. Appl. Phys. 61, 1497–1502 (1987)
Berglund W., Gopinath A.: WKB analysis of bend losses in optical waveguides. IEEE J. Lightwave Technol. 18, 1161–1166 (2000)
Christodoulides D.N., Andreou A.G., Joseph R.I., Westgate C.R.: Analytical calculation of the quantum-mechanical transmission coefficient for a triangular planar-doped potential barrier. Solid-State Electron 28, 821–822 (1985)
Chung M.-S., Kim C.-M.: General eigenvalue equations for optical planar waveguides with arbitrarily graded-index profiles. IEEE J. Lightwave Technol. 18, 878–885 (2000)
Gasiorowicz S.: Quantum Physics, pp. 86–89. Wiley, New York (1974)
Kim C.-M., Chung M.-S.: Eigenvalue equations of N-parallel graded-index waveguides: WKB analysis. IEEE J. Quantum Electron. 33(9), 1608–1613 (1997)
Kim C.-M., Kim Y.-M., Kim W.-K.: Leaky modes of circular slab waveguides: modified Airy functions. IEEE J. Sel. Top. Quantum Electron. 8, 1239–1245 (2002)
Landau L.D., Lifshitz E.M.: Quantum Mechanics. Non-Relativistic Theory, pp. 79–80. Pergamon Press, London (1965)
Langer R.E.: On the asymptotic solutions of ordinary differential equations, with an application to the Bessel functions of large order. Trans. Am. Math. Soc. 33, 23–64 (1931)
Mahapatra P.K., Panchadhyayee P., Bhattacharya S.P., Khan A.: Resonant tunneling in electrically biased multibarrier systems. Phys. B 403, 2780–2788 (2008)
Nakamura K., Shimizu A., Koshiba M., Hayata K.: Finite-element calculation of the transmission probability and the resonant-tunneling lifetime through arbitrary potential barriers. IEEE J. Quantum Electron 27, 1189–1198 (1991)
Panchadhyayee P., Biswas R., Khan A., Mahapatra P.K.: Current density in generalized Fibonacci superlattices under a uniform electric field. J. Phys. Condens. Matter. 20, 275243 (2008)
Powell J.L., Crasemann B.: Quantum Mechanics, pp. 140–153. Addison Wesley, Reading (1962)
Ricco B., Azbel M.: Physics of resonant tunneling. The one-dimensional double-barrier case. Phys. Rev. B 29, 1970–1981 (1984)
Roy S., Ghatak A.K., Goyal I.C., Gallawa R.L.: Modified airy function method for the analysis of tunneling problems in optical waveguides and quantum-well structures. IEEE J. Quantum Electron 29, 340–345 (1993)
Young M., Demas N., Ventrice C.: Analytic calculation of electron transmission probability for planar-doped potential barrier devices. J. Appl. Phys. 71, 498–502 (1992)
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1007/s11082-013-9803-0.
Rights and permissions
About this article
Cite this article
Lee, KT., Jung, E.J., Kim, C.H. et al. Derivation of tunneling probabilities for arbitrarily graded potential barriers using modified Airy functions. Opt Quant Electron 42, 129–141 (2010). https://doi.org/10.1007/s11082-010-9434-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11082-010-9434-7