Skip to main content

Advertisement

SpringerLink
Log in

A two storage production-repairing model with fuzzy defective rate and displayed inventory dependent demand

  • Published:
Optimization and Engineering Aims and scope Submit manuscript

Abstract

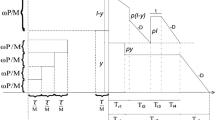
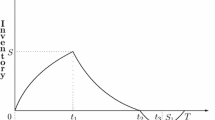
A two storage production-repairing system for a single item with stock-dependent demand is considered. Item is produced with fuzzy defective rate at a production center with a warehouse. Units are bulkly transformed from production center (PC) to a showroom (SR) at the market for sale and excess units are stored at the production center warehouse. After the production period, repairing process is commissioned and then defective units are repaired to new condition before being sold again. Model is formulated as a profit maximization problem using fuzzy differential equation and three different approaches—α-cut of fuzzy average profit, expected value and necessity measure of fuzzy event for defuzzification. A genetic algorithm (GA) with binary mode representation, Roulette wheel selection and random mutation process is used to solve the model. In the first approach, using fuzzy preference ordering of intervals (FPOI), α-cut of fuzzy average profit is optimized using the above GA to derive optimum decisions for the decision maker (DM). In second approach, expected value of average profit is obtained and is optimized using the above GA for optimal decision. In another approach fuzzy objective is directly optimized using necessity measure of fuzzy events for finding marketing decisions. The proposed model is illustrated with numerical examples and results obtained using different approaches are compared.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Allahviranloo T, Shafiee M, Nejatbakhsh Y (2009) A note on “Fuzzy differential equations and the extension principle, Information Sciences”. Inf Sci 179:2049–2051

    Article  MathSciNet  MATH  Google Scholar 

  • Buckley JJ, Feuring T (2000) Fuzzy differential equations. Fuzzy Sets Syst 110:43–54

    Article  MathSciNet  MATH  Google Scholar 

  • Chalco-Cano Y, Roman-Flores H (2009) Comparation between some approaches to solve fuzzy differential equations. Fuzzy Sets Syst 160:1517–1527

    Article  MathSciNet  MATH  Google Scholar 

  • Dobos I, Richter K (2000) The integer EOQ repair and waste disposal model further analysis. Cent Eur J Oper Res 8:173–194

    MathSciNet  MATH  Google Scholar 

  • Dubois D, Prade H (1983) Ranking fuzzy numbers in the setting of possibility theory. Inf Sci 30:183–224

    Article  MathSciNet  MATH  Google Scholar 

  • Dubois D, Prade H (1988) Possibility theory: an approach to computerized processing of uncertainty. Plenum, New York

    Book  MATH  Google Scholar 

  • Giri BC, Pal C, Goswami A, Chaudhuri KS (1996) An inventory model for deteriorating items with stock dependent demand rate. Eur J Oper Res 95:604–610

    Article  MATH  Google Scholar 

  • Goyal SK, Cardenas-Barron LE (2002) Note on economic production quantity model for items with imperfect quality a practical approach. Int J Prod Econ 77:85–87

    Article  Google Scholar 

  • Holland HJ (1975) In: Adaptation in natural and artificial systems. University of Michigan, Ann Arbor

    Google Scholar 

  • Khouja M (1995) The economic production lot size model under volume flexibility. Comput Oper Res 22:515–525

    Article  MATH  Google Scholar 

  • Koh SG, Hwang H, Sohn KI, Ko CS (2002) An optimal ordering and recovery policy for reuseable items. Comput Ind Eng 43:59–73

    Article  Google Scholar 

  • Konstantaras I, Papachristos S (2008) A note on: developing an exact solution for an inventory system with product recovery. Int J Prod Econ 111:707–712

    Article  Google Scholar 

  • Levin RI, Mclaughlin CP, Lamone RP, Kothas JF (1972) Production/operations management: contemporary policy for managing operating systems. McGraw-Hill, New York

    Google Scholar 

  • Liu B, Iwamura K (1998) Chance constraint programming with fuzzy parameters. Fuzzy Sets Syst 94:227–237

    Article  MathSciNet  MATH  Google Scholar 

  • Liu B, Liu YK (2002) Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans Fuzzy Syst 10:445–450

    Article  Google Scholar 

  • Liu Y, Liu B (2003) A class of fuzzy random optimization: expected value models. Inf Sci 155:89–102

    Article  MATH  Google Scholar 

  • Mabini MC, Gelders LF (1991) Repairable item inventory systems: a literature review. Belg J Oper Res Stat Comput Sci 30(4):58–69

    Google Scholar 

  • Maity AK (2011) One machine multiple-product problem with production-inventory system under fuzzy inequality constraint. Appl Soft Comput 11:1549–1555

    Article  Google Scholar 

  • Maiti MK (2008) Fuzzy inventory model with two warehouses under possibility measure on fuzzy goal. Eur J Oper Res 188:746–774

    Article  MathSciNet  MATH  Google Scholar 

  • Maiti MK, Maiti M (2005) Production policy for damageable items with variable cost function in an imperfect production process via genetic algorithm. Math Comput Model 42:977–990

    Article  MathSciNet  MATH  Google Scholar 

  • Maiti MK, Maiti M (2006) Fuzzy inventory model with two warehouses under possibility constraints. Fuzzy Sets Syst 157:52–73

    Article  MathSciNet  MATH  Google Scholar 

  • Mandal M, Maiti M (2000) Inventory of damageable items with variable replenishment and stock-dependent demand. Asia-Pac J Oper Res 17:41–54

    MathSciNet  MATH  Google Scholar 

  • Mandal BN, Phaujdar S (1989) An inventory model for deteriorating items and stock dependent consumption rate. J Oper Res Soc 40:483–488

    Article  MATH  Google Scholar 

  • Mandal S, Maity AK, Maity K, Mondal S, Maiti M (2011) Multi-item multi-period optimal production problem with variable preparation time in fuzzy stochastic environment. Appl Math Model 35(9):4341–4353

    Article  MathSciNet  MATH  Google Scholar 

  • Michalewicz Z (1992) Genetic algorithms + data structures = evolution programs. Springer, Berlin

    MATH  Google Scholar 

  • Mizukoshi MT, Barros LC, Chalco-Cano Y, Roman-Flores H, Bassanezi RC (2007) Fuzzy differential equations and the extension principle. Inf Sci 177:3627–3635

    Article  MathSciNet  MATH  Google Scholar 

  • Omar M, Yeo I (2009) A model for a production-repair system under a time-varying demand process. Int J Prod Econ 119:17–23

    Article  Google Scholar 

  • Porteus EL (1986) Optimal lot sizing, process quality improvement and setup cost reduction. Oper Res 34:137–144

    Article  MATH  Google Scholar 

  • Richter K (1997) Pure and mixed strategies for the EOQ repair and waste disposal problem. OR Spektrum 19:123–129

    Article  MATH  Google Scholar 

  • Roy A, Maity K, Kar S, Maiti M (2009) A production inventory model with remanufacturing for defective and usable items in fuzzy-environment. Comput Ind Eng 56:87–96

    Article  Google Scholar 

  • Salameh MK, Jaber MY (2000) Economic production quantity model for items with imperfect quality. Int J Prod Econ 64:59–64

    Article  Google Scholar 

  • Sengupta A, Pal T (2009) Fuzzy preference ordering of interval numbers in decision problems. Springer, Berlin

    Book  MATH  Google Scholar 

  • Teunter RH (2004) Lot-sizing for inventory systems with product recovery. Comput Ind Eng 46(3):431–441

    Article  Google Scholar 

  • Urban TL (1995) Inventory models with demand rate dependent on stock and shortage levels. Int J Prod Econ 22:85–93

    Google Scholar 

  • Wee HM, Yu J, Chen MC (2007) Optimal inventory model for items with imperfect quality and shortage back ordering. Omega 35:7–11

    Article  Google Scholar 

  • Wu HC (2000) The fuzzy Riemann integral and its numerical integration. Fuzzy Sets Syst 110:1–25

    Article  MATH  Google Scholar 

  • Zadeh LA (1978) Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst 1:3–28

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Mahishadal Girls’ College, Mahishadal, Purba-Medinipur, 721628, West Bengal, India

    Madhab Mondal

  2. Department of Mathematics, Mahishadal Raj College, Mahishadal, Purba-Medinipur, 721628, West Bengal, India

    Manas Kumar Maiti

  3. Department of Applied Mathematics with Oceanology and Computer Programming, Vidyasagar University, Paschim-Medinipur, 721102, West Bengal, India

    Manoranjan Maiti

Authors
  1. Madhab Mondal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manas Kumar Maiti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Manoranjan Maiti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Madhab Mondal.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mondal, M., Maiti, M.K. & Maiti, M. A two storage production-repairing model with fuzzy defective rate and displayed inventory dependent demand. Optim Eng 15, 751–772 (2014). https://doi.org/10.1007/s11081-013-9222-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11081-013-9222-x

Keywords

Search

Navigation