Skip to main content

Advertisement

SpringerLink
Log in

Development of a production inventory model with uncertainty and reliability considerations

  • Published:
Optimization and Engineering Aims and scope Submit manuscript

Abstract

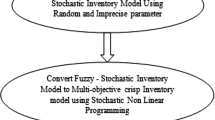
This paper addresses a problem of an imperfect production system under fuzzy demand and inventory holding cost. Production process reliability is considered because of the imperfect production process. In this problem, reliability of the system in regards to producing defective and non-defective items is considered as a decision variable. The objective is to maximize the graded mean integration value (GMIV) of the expected average profit while considering revenues as well as any other relevant costs. The developed model belongs to the class of a geometric programming. We have developed a simple mathematical methodology to solve the model. Genetic algorithm and simulated annealing algorithms are also applied to solve and validate the results. A numerical example has been presented to interpret the solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Bag S, Chakraborty D, Roy AR (2009) A production inventory model with fuzzy random demand and with flexibility and reliability considerations. Comput Ind Eng 56(1):411–416

    Article  Google Scholar 

  • Beightler CS, Phillips DT (1976) Applied geometric programming. Wiley, New York

    MATH  Google Scholar 

  • Chang HC (2004) An application of fuzzy sets theory to the EOQ model with imperfect quality items. Comput Oper Res 31(12):2079–2092

    Article  MathSciNet  MATH  Google Scholar 

  • Cheng TCE (1989) An economic production quantity model with flexibility and reliability consideration. Eur J Oper Res 39(2):174–179

    Article  MATH  Google Scholar 

  • Chen SH, Chang SM (2008) Optimization of fuzzy production inventory model with unrepairable defective products. Int J Prod Econ 113(2):887–894

    Article  Google Scholar 

  • Chen SH, Hsieh CH (1999) Graded mean integration representation of generalized fuzzy numbers. J Chin Fuzzy Syst 5(2):1–7

    Google Scholar 

  • Dubois D, Prade H (1980) Fuzzy sets and systems theory and applications. Academic Press, New York

    MATH  Google Scholar 

  • Duffin RJ, Peterson EL, Zener C (1967) Geometric programming: theory and application. Wiley, New York

    MATH  Google Scholar 

  • Dutta P, Chakraborty D, Roy AR (2007) Continuous review inventory model in mixed fuzzy and stochastic environment. Appl Math Comput 188(1):970–980

    Article  MathSciNet  MATH  Google Scholar 

  • Dutta P, Chakraborty D, Roy AR (2005) A single-period inventory model with fuzzy random variable demand. Math Comput Model 41(8–9):915–922

    Article  MathSciNet  MATH  Google Scholar 

  • Hsieh CH (2002) Optimization of fuzzy production inventory models. Inf Sci 146(1–4):29–40

    Article  MATH  Google Scholar 

  • Kao C, Hsu WK (2002) A single-period inventory model with fuzzy demand. Comput Math Appl 43(6–7):841–848

    Article  MathSciNet  MATH  Google Scholar 

  • Lee HM, Yao JS (1998) Economic production quantity for fuzzy demand quantity, and fuzzy production quantity. Eur J Oper Res 109(1):203–211

    Article  MATH  Google Scholar 

  • Lin CS (1999) Integrated production-inventory models with imperfect production processes and a limited capacity for raw materials. Math Comput Model 29(2):81–89

    Article  MATH  Google Scholar 

  • Lin CS, Chen CH, Kroll DE (2003) Integrated production-inventory models for imperfect production processes under inspection schedules. Comput Ind Eng 44(4):633–650

    Article  Google Scholar 

  • Mohebbi E, Hao D (2008) An inventory model with non-resuming randomly interruptible lead time. Int J Prod Econ 114(2):755–768

    Article  Google Scholar 

  • Panda D, Maiti M (2009) Multi-item inventory models with price dependent demand under flexibility and reliability consideration and imprecise space constraint: a geometric programming approach. Math Comput Model 49(9–10):1733–1749

    Article  MathSciNet  MATH  Google Scholar 

  • Sana SS, Goyal SK, Chaudhuri K (2007) An imperfect production process in a volume flexible inventory model. Int J Prod Econ 105(2):548–559

    Article  Google Scholar 

  • Sarkar B, Moon I (2011) An EPQ model with inflation in an imperfect production system. Appl Math Comput 217(13):6159–6167

    Article  MathSciNet  MATH  Google Scholar 

  • Sarkar B (2012) An inventory model with reliability in an imperfect production process. Appl Math Comput 218(9):4881–4891

    Article  MathSciNet  MATH  Google Scholar 

  • Sana S (2010) A production–inventory model in an imperfect production process. Eur J Oper Res 200(2):451–464

    Article  MathSciNet  MATH  Google Scholar 

  • Wang L, Fu QL, Zeng YR (2012) Continuous review inventory models with a mixture of backorders and lost sales under fuzzy demand and different decision situations. Expert Syst Appl 39(4):4181–4189

    Article  Google Scholar 

  • Wang X (2011) Continuous review inventory model with variable lead time in a fuzzy random environment. Expert Syst Appl 38(9):11715–11721

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial and Production Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh

    Sanjoy Kumar Paul & Abdullahil Azeem

  2. School of Engineering and Information Technology, University of New South Wales, Canberra, Australia

    Sanjoy Kumar Paul, Ruhul Sarker & Daryl Essam

Authors
  1. Sanjoy Kumar Paul
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdullahil Azeem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ruhul Sarker
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daryl Essam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sanjoy Kumar Paul.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Paul, S.K., Azeem, A., Sarker, R. et al. Development of a production inventory model with uncertainty and reliability considerations. Optim Eng 15, 697–720 (2014). https://doi.org/10.1007/s11081-013-9218-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11081-013-9218-6

Keywords

Search

Navigation