Abstract
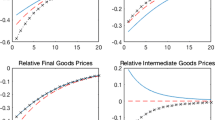
How important are nontradable goods and distribution costs to explain real exchange rate dynamics? We answer this question by estimating a general equilibrium model with intermediate and final tradable and nontradable goods. We find that the estimated model can match characteristics of the data that are relevant in international macroeconomics, such as real exchange rate persistence and volatility, and the correlation between the real exchange rate and other variables. The distinction between tradable and nontradable goods is key to understand real exchange rate fluctuations, but the introduction of distribution costs is not. Nontradable sector technology shocks explain about one third of real exchange rate volatility. We also show that, in order to explain the low correlation between the ratio of relative consumption and the real exchange rates across countries, demand shocks are necessary.




Similar content being viewed by others
Notes
Empirical papers that have estimated fully specified general equilibrium international macroeconomic models include Rabanal and Tuesta (2010), Lubik and Schorfheide (2005), Adolfson et al. (2007), Justiniano and Preston (2010) and De Walque et al. (2006). None of the above mentioned studies consider the role of nontradable goods.
It is impossible to obtain a pure measure of tradable goods inflation. Input-output table data for the U.S. reveals that services are an intermediate input for the production of industrial goods.
Dotsey and Duarte (2008) show that alternative assumptions regarding pricing decisions of firms, namely producer currency pricing (PCP) and local currency pricing (LCP), are not so different for the real exchange rate dynamics.
The convention will be to use an asterisk to denote the counterpart in the foreign country of a variable in the home country (i.e. if aggregate consumption is C in the home country, it will be C ∗ in the foreign country and so on. The same applies to the model’s parameters. When there is potential for confusion we explictly clarify so.
The evolution of net foreign assets over GDP is: \(\beta \widetilde{b}_{t}= \frac{1}{1+g}\widetilde{b}_{t-1}+\frac{X^{f}}{Y}\left( \widetilde{x} _{t}^{h^{\ast }}-\widetilde{x}_{t}^{f}-t_{t}\right) \) where \(\frac{X^{f}}{Y}\) is the imports-GDP ratio, \(\widetilde{x}_{t}^{h^{\ast }}\) is exports of intermediate tradable goods, \(\widetilde{x}_{t}^{f}\) is imports, and t t is the terms of trade. Appendix B details the full set of loglinearized conditions of the model.
That is, the contribution of the “Preference” shock adds up the contribution of the euro area and the U.S. preference shock. The only exception is the demand shock for which we have aggregated across countries and sectors.
Adding the seventies and mid-eighties sample, as in Rabanal and Tuesta (2010), delivers a negative correlation of − 0.17, that a model with incomplete markets and tradable goods can match.
We use HP-filtered data to be able to compare our results with the international real business cycle literature, including Corsetti et al. (2008). The empirical literature interpreted real exchange rate persistence as the slow rate of mean reversion of the real exchange rate. Early examples of applications include Rogoff (1996) and the references therein. A typical result is the strong evidence of slow mean reversion, found by estimating first order autoregressive models for the level of the exchange rate instead of using HP filtered data. For a recent application, see Steinsson (2008).
For robustness, we have also performed an estimation using the terms of trade as an observable variable. Qualitatively, the impulse-responses do not change. Results are available upon request.
We also estimate our model assuming non-separable preferences in line with Monacelli and Perotti (2006). Under this specification we were able to reproduce impulse responses conditional to both fiscal and tradable technology shocks that are consistent with the VAR evidence reported in Monacelli and Perotti (2006) and Corsetti et al. (2006), respectively. Yet, the likelihood decreases substantially and the overall fit of this specification underperforms our benchmark model. Results are available upon request from the authors.
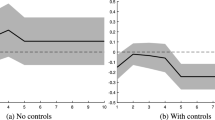
We use the Kalman filter to recover the sequence of shocks. We basically obtain the cyclical components of the change in the real exchange rate associated with each shock, according to our estimated model at its posterior mean.
The additional parameters γ y and the fraction of intermediate goods that is used to produce the final tradable good are taken from Dotsey and Duarte (2008). Hence we calibrate γ y to 0.62, and the fraction of nontradable production that is used as an input in the production of final traded goods to \(\frac{X^{N}}{Y^{N}}=0.4\). We also estimated versions of the two distribution cost models where we estimated those parameters. The qualitative results did not change, and model fit did not improve significantly. In addition to these two parameters, in the model with a distribution sector and sticky prices, we also estimate α T and φ T with the same priors than the other Calvo lotteries and backward looking parameters of Table 1. We also estimate the elasticity of subtitution ε y .
As Benigno (2009) points it out, some restrictions on \(\phi \left(.\right) \) are necessary: \(\phi \left( 0\right) =1;\) assumes the value 1 only if B F,t = 0; differentiable; and decreasing in the neighborhood of zero.
Another way to describe this cost is to assume the existence of intermediaries in the foreign asset market (which are owned by the foreign households) who can borrow and lend to households of country F at a rate ( 1 + r ∗ ), but can borrow from and lend to households of country H at a rate \((1+r^{\ast })\phi \left(.\right)\!.\)
References
Adolfson M, Laseen S , Lindé J, Villani M (2007) Bayesian estimation of an open economy dsge model with incomplete pass-through. J Int Econ 72(2):481–511
An S, Schorfheide F (2007) Bayesian analysis of DSGE models. Econom Rev 26(2–4):113–172
Betts C, Kehoe T (2006) U.S. real exchange rate fluctuations and relative price fluctuations. J Monet Econ 53:1297–1326
Benigno P (2009) Price stability with imperfect financial integration. Journal of Money, Credit and Banking, vol 41(s1). Blackwell Publishing, pp 121–149
Benigno P (2009) Price stability with imperfect financial integration. J Money, Credit Bank 41(1):121–149
Benigno G, Thoenissen C (2008) Consumption and real exchange rates with incomplete markets and non-traded goods. J Int Money Financ 27:926–948
Clarida R, Galí J, Gertler M (2000) Monetary policy rules and macroeconomic stability: evidence and some theory. Q J Econ 115:147–180
Chari VV, Kehoe P, McGrattan E (2002) Can sticky price models generate volatile and persistent real exchange rates? Rev Econ Stud 69:533–563
Corsetti G, Dedola L, Leduc S (2008) International risk sharing and the transmission of productivity shocks. Rev Econ Stud 75(2):443–473
Corsetti G, Dedola L, Leduc S (2006) Productivity, external balance and exchange rates: evidence on the transmission mechanism among G7 countries. Prepared for the 2006 NBER international seminar on macroeconomics
Debaere P, Lee H (2004) The real-side determinants of countries´ terms of trade: a panel data analysis, mimeo. University of Texas, Austin
De Walque G, Smets F, Wouters R (2005) An open economy dsge model linking the euro area and the US economy. Manuscript, National Bank of Belgium and European Central Bank
Dotsey M, Duarte M (2008) Nontradable goods, market segmentation, and exchange rates. J Monet Econ 55(6):1129–1142
Engel C (1999) Accounting for U.S. Real Exchange Rate Changes. Journal of Political Economy, vol 107(3). University of Chicago Press, pp 507–538
Fernández-Villaverde J, Rubio-Ramírez JF (2004) Comparing dynamic equilibrium models to data: a Bayesian approach. J Econ 123:153–187
Galí J, Rabanal P (2005) Technology shocks and aggregate fluctuations: how well does the real business cycle model fit postwar U.S. data?, NBER Chapters. In: NBER macroeconomics annual 2004, vol 19. National Bureau of Economic Research, Inc., pp 225–318
Ireland P (2006) Changes in the federal reserve’s inflation target: causes and consequences. Mimeo, Boston College
Justiniano A, Preston B (2010) Can structural small open economy models account for the influence of foreign disturbances? J Int Econ Elsevier 81(1):61–74
Lubik T, Schorfheide F (2005) A Bayesian look at new open economy macroeconomics, NBER Macroeconomics Annual 2005, pp 313–366
Mandelman F, Rabanal P, Rubio-Ramirez JF, Vilán D (2011) Investment-specific technology shocks and international business cycles: an empirical assessment. Rev Econ Dyn 14(1):136–155
Monacelli T, Perotti R (2006) Fiscal policy, the trade balance, and the real exchange rate: implications for international risk sharing. Mimeo, Universitá Bocconi
Rabanal P, Rubio-Ramírez JF (2005) Comparing new keynesian models of the business cycle: a Bayesian approach. J Monet Econ 52(6):1151–1166
Rabanal P, Rubio-Ramírez JF (2008) Comparing new keynesian models in the euro area: a Bayesian approach. Span Econ Rev 10:23–40
Rabanal P, Tuesta V (2010) Euro-dollar real exchange rate dynamics in an estimated two-country model: an assessment. J Econ Dyn Control 34:780–797
Rogoff K (1996) The purchasing power parity puzzle. J Econ Lit 4:647–68
Schmitt-Grohe S, Uribe M (2011) Business cycles with a common trend in neutral and investment-specific productivity. Rev Econ Dyn 14(1):122–135
Smets F, Wouters R (2003) An estimated dynamic stochastic general equilibrium model of the euro area. Journal of the European Economic Association, vol 1(5). MIT Press, pp 1123–1175
Steinsson J (2008) The dynamic behavior of the real exchange rate in sticky price models. Am Econ Rev 98:519–533
Stockman AC, Tesar LL (1995) Tastes and technology in a two-country model of the business cycle: explaining international comovements. Am Econ Rev 85(1):168–185
Author information
Authors and Affiliations
Corresponding author
Additional information
We wish to thank Pablo Guerrón and Carlos Montoro for helpful discussions, and an anonymous referee for very helpful comments. The opinions expressed in this paper are those of the authors and should not ne attributed to the IMF or IMF policy. Any errors and omissions are our own. Additional material is available in an online appendix at www.paurabanal.net/research.html.
Appendices
Appendix A: The Baseline Model
In this appendix, we present the full version of a model with tradable and nontradable final consumption goods, in the spirit of Stockman and Tesar (1995) and Dotsey and Duarte (2008). We introduce sticky prices in both sectors to be able to study inflation dynamics and their role in affecting the real exchange rate.
1.1 A.1 Households
1.1.1 A.1.1 Preferences
Representative households in the home country are assumed to maximize the following utility function:
subject to the following budget constraint:
E 0 denotes the conditional expectation on information available at date t = 0, β is the intertemporal discount factor, with 0 < β < 1. C t denotes the level of consumption in period t, L t denotes labor supply. The utility function displays external habit formation with respect to the habit stock, which is last period’s aggregate consumption of the economy \(\bar{C}_{t-1}\). \(b\in \lbrack 0,1]\) denotes the importance of the habit stock. φ > 0 is inverse elasticity of labor supply with respect to the real wage. ψ t is a preference shock that follows an AR(1) process in logs
We define the consumption index as
where ε is elasticity of substitution between the final tradable (\(C_{t}^{T}\)) and final nontradable (\(C_{t}^{N}\)) goods, and γ c is the share of final tradable goods in the consumption basket at home.
In this context, the consumer price index that corresponds to the previous specification is given by
where all prices are for goods sold in the home country, in home currency and at consumer level, for both tradable and nontradable goods.
Demands for the final tradable and nontradable goods are given by:
1.1.2 A.1.2 Incomplete Asset Markets
For modelling simplicity, we choose to model incomplete markets with two risk-free one-period nominal bonds denominated in domestic and foreign currency, and a cost of bond holdings is introduced to achieve stationarity. Then, the budget constraint of the domestic households in real units of home currency is given by:
where W t is the nominal wage, and Π t are real profits for the home consumer. \(B_{t}^{H}\) is the holding of the risk free domestic nominal bond and \(B_{t}^{F}\) is the holding of the foreign risk-free nominal bond expressed in foreign country currency. S t is the nominal exchange rate, expressed in units of home country currency per unit of foreign country. The function \(\Phi \left( .\right) \) depends on the net liability position (i.e. the negative net foreign asset position) of the home country, \(\bar{B} _{t}^{F}\), in percent of GDP in the entire economy, and is taken as given by the domestic household.Footnote 16 \(\Phi \left( .\right) \) introduces a convex cost that allows to obtain a well-defined steady state, and captures the costs of undertaking positions in the international asset market.Footnote 17
1.2 A.2 Production Sector
The production of this economy is undertaken by three sectors. First, there is a final goods sector, that uses intermediate tradable inputs from both countries and operates under perfect competition, to produce the final tradable goods. This same sector also aggregates varieties of the nontradable goods to produce a final nontradable good that is sold to households. The second sector produces intermediate tradable goods, which are used as an input for the production of final goods both in the home and in the foreign country. The third sector produces nontradable goods, that are used as inputs in the production of the final nontradable good.
1.2.1 A.2.1 Final Goods Sector
The final tradable good is consumed by domestic households. This good is produced by a continuum of firms, each producing the same variety, labelled by \(Y_{t}^{T}\), using intermediate home \(\left( X_{t}^{h}\right) \) and foreign \(\left( X_{t}^{f}\right) \) goods with the following technology:
where θ is the elasticity of substitution between home-produced and foreign-produced imported intermediate goods, and γ x is the share of home goods in the production function. We further assume symmetric home-bias in the composite of intermediate tradable goods. The corresponding composite of home and foreign intermediate tradable goods abroad is given by
\(X_{t}^{h}\) and \(X_{t}^{f}\), that denote the amount of home and foreign intermediate tradable inputs to produce the final tradable good at home, are also Dixit-Stiglitz aggregates of all types of home and foreign final goods, with elasticity of substitution σ:
and
where \(X_{t}^{h}(h)\) and \(X_{t}^{f}(f)\) denote individual quantities from intermediate tradable goods producers at home and foreign. The equivalent quantities for foreign final tradable goods producers are \(X_{t}^{h^{\ast }}(h)\) and \(X_{t}^{f^{\ast }}(f)\). Optimizing conditions by final tradable goods producers deliver the following demand functions:
where
and
We assume that the law of one price holds for intermediate inputs, such that \(P_{t}^{h}(h)=P_{t}^{h^{\ast }}(h)S_{t}\), and \(P_{t}^{f}(f)=P_{t}^{f^{\ast }}(f)S_{t}\), where S t is the nominal exchange rate.
The production of the final nontradable good is given by:
where we assume the same elasticity σ > 1 than in the case of final tradable goods produced within country H. The price level for nontradables is
1.2.2 A.2.2 Intermediate Non-Tradable Goods Sector
The intermediate nontradable sector produces differentiated goods that are aggregated by final good producing firms, and ultimately used for final consumption by domestic households only. Each firm produces intermediate nontradable goods according to the following production function
where A t is a labor augmenting aggregate world technology shock which has a unit root with drift, as in Galí and Rabanal (2005):
This shock also affects the intermediate tradable sector production function. Hence, real variables in both countries grow at a rate g. \( Z_{t}^{N}\) is the country-specific productivity shock to the nontradable sector at time t which evolves according to an AR(1) process in logs
Firms in the nontradable sector face a Calvo lottery when setting their prices. Each period, with probability 1 − α N , firms receive a stochastic signal that allows them to reset prices optimally. We assume that there is partial indexation with a coefficient φ N to last period’s sectorial inflation rate for those firms that do not get to reset prices. As a result, firms maximize the following profits function:
subject to
where \(Y_{t}^{N,d}\left( n\right) \) is total individual demand for a given type of nontradable good n, and \(Y_{t}^{N}\) is aggregate demand for nontradable goods, as defined above. \(\Lambda _{t,t+k}=\beta ^{k}\frac{ \lambda _{t+k}}{\lambda _{t}}\) is the stochastic discount factor, where \( \lambda _{t}=\frac{\psi _{t}}{C_{t}-bC_{t-1}}\) is the marginal utility of consumption. \(MC_{t}^{N}\) corresponds to the real marginal cost in the nontradable sector. From cost minimization:
1.2.3 A.2.3 Intermediate Tradable Goods Sector
The intermediate tradable sector produces differentiated goods that are sold to the final sector goods producers in the home and foreign countries. Most functional forms are similar to those presented for the nontradable sector.
Each firm produces tradable intermediate goods according to the following production function
where \(Z_{t}^{h}\) is the country-specific productivity shock to the intermediate goods tradable sector at time t which evolves according to an AR(1) process in logs
Firms in the intermediate tradable sector face the same Calvo lottery as firms in the intermediate nontradable sector, with relevant parameters α h and φ h :
subject to
where \(Y_{t}^{h,d}\left( h\right) \) is total individual demand for a given type of tradable intermediate good h, and \(X_{t}^{h}\) is aggregate demand for intermediate good h, consisting of home demand, and foreign demand:
\(MC_{t}^{h}\) corresponds to the real marginal cost in the nontradable sector. From cost minimization:
1.2.4 A.2.4 Market Clearing
We assume that the demand shock is allocated between tradable and nontradable goods in the same way that private consumption is. Hence the market clearing conditions for both types of final goods, consisting of private consumption and the demand shock in the tradadable sector, are:
where \(G_{t}^{N},G_{t}^{T}\) follow AR(1) processes in logs. The bond market clearing conditions are
For the nontradable intermediate goods, the market clearing condition is:
while for the intermediate tradable goods sector it is:
For the labor market:
1.3 A.3 Optimizing, Market Clearing Conditions, and Monetary Policy
In this subsection we present the full set of equations characterizing the symmetric equilibrium. Since all agents in each economy are equal, then the per capita and aggregate consumption levels are equal (\(C_{t}=\bar{C}_{t}\)), as well as the net foreign assets levels (\(B_{t}^{F}=\bar{B}_{t}^{F}\)).
1.3.1 A.3.1 Households
The Euler equations for home and foreign households, and the optimal condition of holdings by home household of the foreign bond are:
where λ t is the marginal utility of consumption:
The labor supply decisions in each country are:
where:
and
Household demand for final tradable and nontradable goods are given by:
and the CPI’s in each country are given by:
The real exchange rate is
1.3.2 A.3.2 Final Goods Producers
The production of final tradable goods in both countries is given by:
and
Demand for intermediate tradable goods is:
where
The price of final tradable goods is:
and
Since we assumed that the law of one price holds for intermediate goods, it also holds in the aggregate, such that \(P_{t}^{h}=P_{t}^{h^{\ast }}S_{t}\), and \(P_{t}^{f}=P_{t}^{f^{\ast }}S_{t}\), where S t is the nominal exchange rate.
1.3.3 A.3.3 Nontradable Goods Producers
The price setting equations are given by the following optimal expressions:
where
The evolution of the price level of nontradables is
where \(\Pi _{t-1}^{N}=\frac{P_{t-1}^{N}}{P_{t-2}^{N}}\).
The production function is:
In the foreign country these expressions are:
where
The evolution of the price level of nontradables is
where \(\Pi _{t-1}^{N^{\ast }}=\frac{P_{t-1}^{N^{\ast }}}{P_{t-2}^{N^{\ast }}} \).
The production function is:
1.3.4 A.3.4 Intermediate Traded Goods Producers
The price setting equations are given by the following optimal expressions:
where
The evolution of the price level of final tradables is
where \(\Pi _{t-1}^{h}=\frac{P_{t-1}^{h}}{P_{t-2}^{h}}\).
The production function is:
In the foreign country, this expressions are:
where
The evolution of the price level of final tradables is
where \(\Pi _{t-1}^{f^{\ast }}=\frac{P_{t-1}^{f^{\ast }}}{P_{t-2}^{f^{\ast }}} \).
The production function is:
1.3.5 A.3.5 Monetary Policy
Monetary policy in both countries is conducted with a Taylor rule that targets CPI inflation and output growth deviation from steady-state values:
1.3.6 A.3.6 Demand Shocks
1.3.7 A.3.7 Trade Balance and Net Foreign Asset Dynamics
We present the evolution of the trade balance and net foreign assets of the home country, since the definition those in the foreign country will mirror those in the home country. Holdings of foreign bonds depend on the trade balance (NX t ) as follows
Since international trade only occurs at the intermediate goods level, net exports equal exports minus imports of intermediate goods:
Finally, we define nominal GDP to be equal to aggregate nominal private and public consumption, hence \( P_{t}Y_{t}=P_{t}^{T}(C_{t}^{T}+G_{t}^{T})+P_{t}^{N}(C_{t}^{N}+G_{t}^{N})\).
Appendix B: Log-Linear Version of the Model
Euler equations
Risk sharing
where \(\chi \equiv -\Phi ^{\prime }\left( 0\right) Y,\) \(b_{t}=\left( \frac{ S_{t}B_{t}^{F}}{P_{t}}\right) Y^{-1}.\)
The labor supply schedules are given by:
Technology
Consumer price inflation
Tradable inflation
Price setting in the nontradable sector
where \(\kappa _{N}=\left( 1-\alpha _{N}\right) \left( 1-\beta \alpha _{N}\right) /\alpha _{N},\) \(\kappa _{N^{\ast }}=\left( 1-\alpha _{N^{\ast }}\right) \left( 1-\beta \alpha _{N^{\ast }}\right) /\alpha _{N^{\ast }},\) \( t^{N}=p_{t}^{N}-p_{t},\) and \(t^{N^{\ast }}=p_{t}^{N^{\ast }}-p_{t}\).
Price setting in the intermediate tradable good sector
where \(\kappa _{h}=\left( 1-\alpha _{h}\right) \left( 1-\beta \alpha _{h}\right) /\alpha _{h},\) \(\kappa _{f^{\ast }}=\left( 1-\alpha _{f^{\ast }}\right) \left( 1-\beta \alpha _{f^{\ast }}\right) /\alpha _{f^{\ast }},t_{t}^{h}=p_{t}^{h}-p_{t}^{T},t_{t}^{f^{\ast }}=p_{t}^{f^{\ast }}-p_{t}^{T^{\ast }},\) \(t^{T}=p_{t}^{T}-p_{t},\) and \(t^{T^{\ast }}=p_{t}^{T^{\ast }}-p_{t}\).
Final consumption demand
Intermediate tradable and nontradable demand
Relative Price Index
Let’s define \(t_{t}=\frac{p_{t}^{f}}{p_{t}^{h}}\), since the law of one price holds \(t_{t}=-t_{t}^{\ast }=\frac{p_{t}^{h^{\ast }}}{p_{t}^{f^{\ast }}},\) then we can write the following relative prices as a function of t t .
Relative prices
Taylor rules
Net foreign assets and net exports
where \(\widetilde{b}_{t}=\frac{\bar{B}_{t}^{F}S_{t}}{P_{t}Y}\) is the debt to GDP ratio, and \(\widetilde{nx}_{t}=\frac{NX_{t}}{Y}\), and where we have assumed balanced trade in the steady state. To solve for the steady-state ratios, we have that:
Therefore tradable GDP over total GDP is
Hence
Market clearing:
where γ equals the fraction of government spending over total output. For the nontradable good, the market clearing condition is:
Finally, for the intermediate tradable goods sector:
Total real GDP
total labor
For the foreign country:
Mapping variables in the model with observable variables.
Shocks
and \(\varepsilon _{t}^{a},\varepsilon _{t}^{r},\varepsilon _{t}^{r^{\ast }}\) are iid shocks.
Rights and permissions
About this article
Cite this article
Rabanal, P., Tuesta, V. Nontradable Goods and the Real Exchange Rate . Open Econ Rev 24, 495–535 (2013). https://doi.org/10.1007/s11079-012-9250-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11079-012-9250-8