Abstract
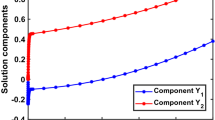
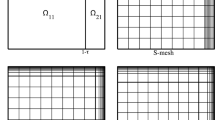
We consider a coupled system of first-order singularly perturbed quasilinear differential equations with given initial conditions. The leading term of each equation is multiplied by a distinct small positive parameter, which induces overlapping layers. The quasilinear system is discretized by using first and second order accurate finite difference schemes for which we derive general error estimates in the discrete maximum norm. As consequences of these error estimates we establish nodal convergence of O((N −1 lnN)p),p=1,2, on the Shishkin mesh and O(N −p),p=1,2, on the Bakhvalov mesh, where N is the number of mesh intervals and the convergence is robust in all of the parameters. Numerical computations are included which confirm the theoretical results.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Athanasios, A.C.: Approximation of Large-Scale Dynamical Systems. SIAM, Philadelphia (2005)
de Boor, C.: Good approximation by splines with variable knots. In: Meir, A., Sharma, A. (eds.) Spline Functions and Approximation Theory, Proceedings of the Symposium held at the University of Alberta, Edmonton, May 29–June 1, 1972. Birkhauser, Basel (1973)
Cen, Z., Xu, A., Le, A.: A second-order hybrid finite difference scheme for a system of singularly perturbed initial value problems. J. Comput. Appl. Math. 234, 3445–3457 (2010)
Chang, K.W., Howes, F.A.: Nonlinear Singular Perturbation Phenomena. Springer, New York (1984)
Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Robust computational techniques for boundary layers. Chapman & Hall/CRC, Boca Raton, Florida (2000)
Gajić, Z., Lim, M.T.: Optimal Control of Singularly Perturbed Linear Systems and Applications. Marcel Dekker, New York (2001)
Kumar, S., Kumar, M.: Parameter-robust numerical method for a system of singularly perturbed initial value problems. Numer. Algorithms 59, 185–195 (2012)
Ladde, G., Lakshmikantham, V., Vatsala, A.: Monotone Iterative Techniques for Nonlinear Differential Equations. Pitman, Boston (1985)
Linss, T.: Sufficient conditions for uniform convergence on layer-adapted grids. Appl. Numer. Math. 37, 241–255 (2001)
Linss, T.: Layer-Adapted Meshes for Reaction-Convection-Diffusion Problems. Vol. 95 of Lecture Notes in Mathematics. Springer, Berlin (2010)
Meenakshi, P.M., Valarmathi, S., Miller, J.J.H.: Solving a partially singularly perturbed initial value problem on shishkin meshes. Appl. Math. Comput. 215, 3170–3180 (2010)
Rao, S.C.S., Kumar, S.: Second order global uniformly convergent numerical method for a coupled system of singularly perturbed initial value problems. Appl. Math. Comput. 219, 3740–3753 (2012)
Roos, H.G., Stynes, M., Tobiska, L.: Robust numerical methods for singularly perturbed differential equations. In: Springer Series in Computational Mathematics. 2nd edn. Springer-Verlag, Berlin (2008)
Valarmathi, S., Miller, J.J.H.: A parameter-uniform finite difference method for singularly perturbed linear dynamical systems. Int. J. Numer. Anal. Mod. 7, 535–548 (2010)
Varga, R.S.: Matrix Iterative Analysis. Prentice-Hall, Englewood Cliffs, N.J (1962)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kumar, S., Kumar, M. Analysis of some numerical methods on layer adapted meshes for singularly perturbed quasilinear systems. Numer Algor 71, 139–150 (2016). https://doi.org/10.1007/s11075-015-9989-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-015-9989-2