Internal resonance in the higher-order modes of a MEMS beam: experiments and global analysis

Abstract

This work investigates the dynamics of a microbeam-based MEMS device in the neighborhood of a 2:1 internal resonance between the third and fifth vibration modes. The saturation of the third mode and the concurrent activation of the fifth are observed. The main features are analyzed extensively, both experimentally and theoretically. We experimentally observe that the complexity induced by the 2:1 internal resonance covers a wide driving frequency range. Constantly comparing with the experimental data, the response is examined from a global perspective, by analyzing the attractor-basins scenario. This analysis is conducted both in the third-mode and in fifth-mode planes. We show several metamorphoses occurring as proceeding from the principal resonance to the 2:1 internal resonance, up to the final disappearance of the resonant and non-resonant attractors. The shape and wideness of all the basins are examined. Although they are progressively eroded, an appreciable region is detected where the compact cores of the attractors involved in the 2:1 internal resonance remain substantial, which allows effectively operating them under realistic conditions. The dynamical integrity of each resonant branch is discussed, especially as approaching the bifurcation points where the system becomes more vulnerable to the dynamic pull-in instability.

Appendix 1: Problem formulation

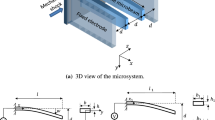
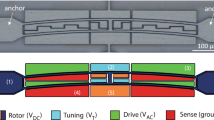
The device is modeled as a parallel plate capacitor, as represented in the schematic in Fig. 18. The microbeam is described in the framework of the Euler–Bernoulli theory. Axial and transversal displacements are denoted as w(z, t) and v(z, t), respectively. Along the vertical axis, we consider as positive direction the one toward the substrate. The microbeam is assumed of length L, width b, and thickness h (sum of all its layers). It is characterized by a straight configuration, constant rectangular cross section, and fixed–fixed boundary conditions. Residual stresses are represented by a constant axial load P, which induces axial displacement at the right end B. Since the lower electrode spans half the length of the microbeam, only this part contributes to the electric force term.

Fig. 18

Schematic of the device mechanical model

The governing equation of motion becomes [1]

$$\ddot{v}+\xi \dot{v}+v^{{\prime \prime \prime \prime}}+\alpha v^{\prime \prime}=-\gamma {F}_{e}$$

(A.1)

where

$$\alpha =n-ka{\int }_{0}^{1}{\frac{1}{2}\left({v}^{{{\prime}}}\right)}^{2}{\text{d}}z$$

(A.2)

and the electric force term is

$${F}_{e}=\frac{{({V}_{\text{DC}}+{V}_{\text{AC}}{\mathrm{cos}}(\varOmega t))}^{2}}{{(1-v)}^{2}}[U\left({z}_{1}\right)-U({z}_{2})]$$

(A.3)

where $U\left({z}_{1}\right)$ and $U\left({z}_{2}\right)$ are the unit step functions defining the lower electrode length and position. The boundary conditions are

$$ v(0,{ }t) = 0\quad v(1,{ }t) = 0\quad v^{{\prime}}(0,{ }t) = 0\quad v^{{\prime}}(1,{ }t) = 0 $$

(A.4)

In Eqs. (A.1)–(A.4), primes denote derivatives with respect to z, and dots denote derivatives with respect to t. The nondimensional variables are (denoted by tilde signs, which are dropped in (A.1)–(A.4) for convenience)

$$ \tilde{z} = \frac{z}{L}\quad \tilde{v} = \frac{v}{d}\quad \tilde{t} = \frac{t}{T} $$

(A.5)

and the nondimensional parameters are

$$ \begin{array}{*{20}l} {ka = (EA)d^{2} /(EJ)} \hfill & {n = (EA)Lw_{B} /(EJ)} \hfill \\ {\gamma = \frac{1}{2}\varepsilon_{0} \varepsilon_{\text{r}} A_{c} L^{3} /\left( {d^{3} EJ} \right)} \hfill & {\xi = cL^{4} /(EJT)} \hfill \\ {T = \sqrt {\left( {\rho AL^{4} } \right)/(EJ)} } \hfill & {\tilde{\varOmega } = \varOmega T} \hfill \\ \end{array} $$

(A.6)

where EA is the axial stiffness, EJ is the bending stiffness, A is the area of the cross section, J is its moment of inertia, E is the effective Young’s modulus, ρ is the material density, d is the equivalent capacitor gap distance between the stationary electrode and the movable one, A_c is the overlapping area between the lower and the upper electrode (half-electrode configuration), c is the viscous damping coefficient, w_B is the axial displacement at the right end B, ε₀ is the dielectric constant in the free space, and ε_r is the relative permittivity of the gap space medium with respect to the free space.

The nondimensional axial force n and the time T are identified by referring to the linear part of Eq. (A.1) and matching the first two natural frequencies, which yields n = -145.5 (traction), and T = 0.0000513797.

Assuming these values, the first seven theoretical natural frequencies are estimated as: f₁ = 145.2 kHz (first symmetric), f₂ = 315.132 kHz (first antisymmetric), f₃ = 526.637 kHz (second symmetric), f₄ = 788.747 kHz (second antisymmetric), f₅ = 1106.05 kHz (third symmetric), f₆ = 1480.95 kHz (third antisymmetric), f₇ = 1914.77 kHz (fourth symmetric). Up to f₅, the theoretical values are very close to the experimental ones. This is even though the identification is conducted using only the first two natural frequencies.

Regarding the gap, the upper electrode is constituted by the conductive layer of gold/chrome applied on top of the microbeam; the silicon nitride (Si₃N₄), instead, is a dielectric material. For this reason, we consider the equivalent capacitor gap [67], which is composed of the air gap plus the contribution due to the silicon nitride layer, whose dielectric constant is  ${\varepsilon }_{{\mathrm{rSi}}_{3}{\mathrm{N}}_{4}}$ = 7 [68]. Thus, the equivalent capacitor gap is

$$d={d}_{\mathrm{air}}+\frac{{t}_{\mathrm{Si}3{\mathrm{N}}4}}{{\varepsilon }_{\mathrm{rSi}3{\mathrm{N}}4}}=2.714 \upmu{\text{m}}$$

(A.7)

Regarding the parameter ka, this is evaluated by assuming the microbeam of homogeneous isotropic material (silicon nitride) and by referring to the equivalent capacitor gap, which yields ka = 28.868. For the parameter γ, we assume γ = 0.08; this value is slightly higher than the one extracted by matching the distance between the resonant and non-resonant branch of the principal attractors; this allows better observing the underlying phenomena. For the damping, we assume $\xi$ = 0.053; also this value is slightly more elevated than the one extracted by matching (as far as possible) the lengthening of the principal resonant branch at small ${V}_{\text{AC}}$. This increment is deliberately added since calculating the attractor-basins phase portraits is computationally very demanding, and the higher damping facilitates the convergence of the trajectories to the corresponding attractors.

To derive the reduced-order model, we approximate the microbeam deflection as $v(z, t)\cong {\sum }_{i=1}^{n}{\phi }_{i}(z){u}_{i}(t)$, where ${\phi }_{i}(z)$ are the corresponding mode shapes, normalized as ${\int }_{0}^{1}{\phi }_{i}{\phi }_{j}{\mathrm{d}}z={\delta }_{ij}$. Considering the third and fifth modes and applying the Galerkin method [69, 70], the 2 d.o.f. Galerkin reduced-order model becomes

$$\begin{aligned}&{\ddot{u}}_{n}+c{\dot{u}}_{n}+{\omega }_{n}^{2}{u}_{n}-ka\left({a}_{n1}{u}_{1}^{3}+{a}_{n2}{u}_{2}^{3}+{a}_{n3}{u}_{1}{u}_{2}^{2}+{a}_{n4}{u}_{2}{u}_{1}^{2}\right)\\&\quad=-\gamma {V}^{2}{\int }_{0}^{0.5}\frac{{\phi }_{n}}{{\left(1-{\phi }_{1}{u}_{1}-{\phi }_{2}{u}_{2}\right)}^{2}}{\mathrm{d}}z\quad {\mathrm{for}}\,\,n = 1, 2\end{aligned}$$

(A.8)

where the first equation (n = 1) refers to the third mode and the second (n = 2) to the fifth. The electric force term is integrated numerically. The obtained coefficients are reported in Table 2.

Table 2 Coefficients of the 2 d.o.f. Galerkin reduced-order model