Abstract
This work investigates the dynamics of a microbeam-based MEMS device in the neighborhood of a 2:1 internal resonance between the third and fifth vibration modes. The saturation of the third mode and the concurrent activation of the fifth are observed. The main features are analyzed extensively, both experimentally and theoretically. We experimentally observe that the complexity induced by the 2:1 internal resonance covers a wide driving frequency range. Constantly comparing with the experimental data, the response is examined from a global perspective, by analyzing the attractor-basins scenario. This analysis is conducted both in the third-mode and in fifth-mode planes. We show several metamorphoses occurring as proceeding from the principal resonance to the 2:1 internal resonance, up to the final disappearance of the resonant and non-resonant attractors. The shape and wideness of all the basins are examined. Although they are progressively eroded, an appreciable region is detected where the compact cores of the attractors involved in the 2:1 internal resonance remain substantial, which allows effectively operating them under realistic conditions. The dynamical integrity of each resonant branch is discussed, especially as approaching the bifurcation points where the system becomes more vulnerable to the dynamic pull-in instability.

















Similar content being viewed by others
References
Younis, M.I.: MEMS Linear and Nonlinear Statics and Dynamics. Springer, New York (2011)
Ruzziconi, L., Lenci, S., Younis, M.I.: An imperfect microbeam under an axial load and electric excitation: nonlinear phenomena and dynamical integrity. Int. J. Bifurc. Chaos 23(2), 1350026 (2013)
Ramini, A., Hennawi, Q., Younis, M.I.: Theoretical and experimental investigation of the nonlinear behavior of an electrostatically actuated in-plane MEMS arch. J. Microelectromech. Syst. 25(3), 570–578 (2016)
Medina, L., Gilat, R., Krylov, S.: Dynamic release condition in latched curved micro beams. Commun. Nonlinear. Sci. Numer. Simul. 73, 291–306 (2019)
Kambali, P.N., Torres, F., Barniol, N., Gottlieb, O.: Nonlinear multi-element interactions in an elastically coupled microcantilever array subject to electrodynamic excitation. Nonlinear Dyn. 98, 3067–3094 (2019)
Bassinello, D.G., Tusset, A.M., Rocha, R.T., Balthazar, J.M.: Dynamical analysis and control of a chaotic microelectromechanical resonator model. Shock Vib. 2018, 4641629 (2018)
Kumar, V., Boley, J.W., Yang, Y., Ekowaluyo, H., Miller, J.K., Chiu, G.T.C., Rhoads, J.F.: Bifurcation-based mass sensing using piezoelectrically-actuated microcantilevers. Appl. Phys. Lett. 98(15), 153510 (2011)
Ouakad, H.M., Najar, F.: Nonlinear dynamics of MEMS arches assuming out-of-plane actuation arrangement. J. Vib. Acoust. 141(4), 041010 (2019)
Hafiz, M.A.A., Kosuru, L., Younis, M.I.: Electrothermal frequency modulated resonator for mechanical memory. J. Microelectromech. Syst. 25(5), 877–883 (2016)
Samanta, C., Arora, N., Naik, A.K.: Tuning of geometric nonlinearity in ultrathin nanoelectromechanical systems. Appl. Phys. Lett. 113, 113101 (2018)
Kacem, N., Baguet, S., Duraffourg, L., Jourdan, G., Dufour, R., Hentz, S.: Overcoming limitations of nanomechanical resonators with simultaneous resonances. Appl. Phys. Lett. 107(7), 073105 (2015)
Jaber, N., Ilyas, S., Shekhah, O., Eddaoudi, M., Younis, M.I.: Resonant gas sensor and switch operating in air with metal–organic frameworks coating. J. Microelectromech. Syst. 27(2), 156–163 (2018)
Hajjaj, A.Z., Jaber, N., Ilyas, S., Alfosail, F.K., Younis, M.I.: Linear and nonlinear dynamics of micro and nano-resonators: review of recent advances. Int. J. Non-Linear Mech. 119, 103328 (2020)
Asadi, K., Yu, J., Cho, H.: Nonlinear couplings and energy transfers in micro-and nano-mechanical resonators: intermodal coupling, internal resonance and synchronization. Philos. Trans. R. Soc. A 376(2127), 20170141 (2018)
Hajjaj, A.Z., Jaber, N., Hafiz, M.A.A., Ilyas, S., Younis, M.I.: Multiple internal resonances in MEMS arch resonators. Phys. Lett. A 382(47), 3393–3398 (2018)
Hacker, E., Gottlieb, O.: Application of reconstitution multiple scale asymptotics for a two-to-one internal resonance in magnetic resonance force microscopy. Int. J. Non-Linear Mech. 94, 174–199 (2017)
Yang, W., Towfighian, S.: Internal resonance and low frequency vibration energy harvesting. Smart Mater. Struct. 26(9), 095008 (2017)
Kirkendall, C.R., Howard, D.J., Kwon, J.W.: Internal resonance in quartz crystal resonator and mass detection in nonlinear regime. Appl. Phys. Lett. 103(22), 223502 (2013)
Sarrafan, A., Azimi, S., Golnaraghi, F., Bahreyni, B.: A nonlinear rate microsensor utilising internal resonance. Sci. Rep. 9(1), 8648 (2019)
Vyas, A., Peroulis, D., Bajaj, A.K.: Dynamics of a nonlinear microresonator based on resonantly interacting flexural–torsional modes. Nonlinear Dyn. 54(1–2), 31–52 (2008)
Potekin, R., Dharmasena, S., Keum, H., Jiang, X., Lee, J., Kim, S., Bergman, L.A., Vakakis, A.F., Cho, H.: Multi-frequency atomic force microscopy based on enhanced internal resonance of an inner-paddled cantilever. Sens. Actuator A Phys. 273, 206–220 (2018)
Alfosail, F.K., Hajjaj, A.Z., Younis, M.I.: Theoretical and experimental investigation of two-to-one internal resonance in MEMS arch resonators. J. Comput. Nonlinear Dyn. 14(1), 011001 (2019)
Daqaq, M.F., Abdel-Rahman, E.M., Nayfeh, A.H.: Two-to-one internal resonance in microscanners. Nonlinear Dyn. 57, 231 (2009)
Nathamgari, S.S.P., Dong, S., Medina, L., Moldovan, N., Rosenmann, D., Divan, R., Lopez, D., Lauhon, L.J., Espinosa, H.D.: Nonlinear mode coupling and one-to-one internal resonances in a monolayer WS2 nanoresonator. Nano Lett. 19(6), 4052–4059 (2019)
Ruzziconi, L., Jaber, N., Kosuru, L., Bellaredj, M.L., Younis, M.I.: Two-to-one internal resonance in the higher-order modes of a MEMS beam: experimental investigation and theoretical analysis via local stability theory. Int. J. Non-Linear Mech. 129, 103664 (2021)
Ruzziconi, L., Lenci, S., Younis, M.I.: Interpreting and predicting experimental responses of micro-and nano-devices via dynamical integrity. In: Lenci, S., Rega, G. (eds.) Global Nonlinear Dynamics for Engineering Design and System Safety, pp. 113–166. Springer, Cham (2019)
Alneamy, A.M., Khater, M.E., Abdel-Aziz, A.K., Heppler, G.R., Abdel-Rahman, E.M.: Electrostatic arch micro-tweezers. Int. J. Non-Linear Mech. 118, 103298 (2020)
Nguyen, V.N., Baguet, S., Lamarque, C.-H., Dufour, R.: Bifurcation-based micro-/nanoelectromechanical mass detection. Nonlinear Dyn. 79(1), 647–662 (2015)
Alcheikh, N., Hajjaj, A.Z., Younis, M.I.: Highly sensitive and wide-range resonant pressure sensor based on the veering phenomenon. Sens. Actuator A Phys. 300, 111652 (2019)
Westra, H., Poot, M., Van Der Zant, H., Venstra, W.: Nonlinear modal interactions in clamped-clamped mechanical resonators. Phys. Rev. Lett. 105, 117205 (2010)
Venstra, W.J., Capener, M.J., Elliott, S.R.: Nanomechanical gas sensing with nonlinear resonant cantilevers. Nanotechnology 25, 425501 (2014)
Kozinsky, I., Postma, H.W.C., Kogan, O., Husain, A., Roukes, M.L.: Basins of attraction of a nonlinear nanomechanical resonator. Phys. Rev. Lett. 99(20), 207201 (2007)
Lenci, S., Rega, G.: Control of pull-in dynamics in a nonlinear thermoelastic electrically actuated microbeam. J. Micromech. Microeng. 16(2), 390 (2006)
Settimi, V., Rega, G.: Exploiting global dynamics of a noncontact atomic force microcantilever to enhance its dynamical robustness via numerical control. Int. J. Bifurc. Chaos 26(07), 1630018 (2016)
Ruzziconi, L., Younis, M.I., Lenci, S.: An electrically actuated imperfect microbeam: dynamical integrity for interpreting and predicting the device response. Meccanica 48(7), 1761–1775 (2013)
Ruzziconi, L., Lenci, S., Younis, M.I.: Dynamical integrity for interpreting experimental data and ensuring safety in electrostatic MEMS. In: Wiercigroch, M., Rega, G. (eds.) IUTAM Symposium on Nonlinear Dynamics for Advanced Technologies and Engineering Design, pp. 249–261. Springer, Dordrecht (2013)
Thompson, J.M.T., Stewart, H.B.: Nonlinear Dynamics and Chaos. Wiley, New York (2002)
Jaber, N., Ramini, A., Carreno, A.A.A., Younis, M.I.: Higher-order modes excitation of electrostatically actuated clamped–clamped microbeams: experimental and analytical investigation. J. Micromech. Microeng. 26, 025008 (2016)
Ewins, D.J.: Modal Testing: Theory, Practice and Application. Wiley, New York (2009)
Rhoads, J., Shaw, S.W., Turner, K.L.: Nonlinear dynamics and its applications in micro- and nanoresonators. J. Dyn. Syst. Meas. Control 132(3), 034001 (2010)
Rocha, R.T., Balthazar, J.M., Tusset, A.M., Piccirillo, V., Felix, J.L.P.: Nonlinear piezoelectric vibration energy harvesting from a portal frame with two-to-one internal resonance. Meccanica 52, 2583–2602 (2017)
Lan, C., Qin, W., Deng, W.: Energy harvesting by dynamic unstability and internal resonance for piezoelectric beam. Appl. Phys. Lett. 107, 093902 (2015)
Hacker, E., Gottlieb, O.: Internal resonance based sensing in noncontact atomic force microscopy. Appl. Phys. Lett. 101(5), 053106 (2012)
Vyas, A., Peroulis, D., Bajaj, A.K.: A microresonator design based on nonlinear 1:2 internal resonance in flexural structural modes. J. Microelectromech. Syst. 18, 744–762 (2009)
Jeong, B., Pettit, C., Dharmasena, S., Keum, H., Lee, J., Kim, J., Kim, S., McFarland, D.M., Bergman, L.A., Vakakis, A.F., Cho, H.: Utilizing intentional internal resonance to achieve multi-harmonic atomic force microscopy. Nanotechnology 27(12), 125501 (2016)
Noori, N., Sarrafan, A., Golnaraghi, F., Bahreyni, B.: Utilization of 2:1 internal resonance in microsystems. Micromachines 9(9), 448 (2018)
Nayfeh, A., Mook, D.: Nonlinear Oscillations. Wiley, New York (1979)
Alsaleem, F.M., Younis, M.I., Ruzziconi, L.: An experimental and theoretical investigation of dynamic pull-in in MEMS resonators actuated electrostatically. J. Microelectromech. Syst. 19(4), 794–806 (2010)
Ruzziconi, L., Ramini, A.H., Younis, M.I., Lenci, S.: Theoretical prediction of experimental jump and pull-in dynamics in a MEMS sensor. Sensors 14(9), 17089–17111 (2014)
Hsu, C.S.: Cell-to-Cell Mapping. A Method of Global Analysis for Nonlinear Systems. Springer, Berlin (1987)
Thompson, J.M.T.: Chaotic phenomena triggering the escape from a potential well. Proc. R. Soc. Lond. A 421, 195–225 (1989)
Rega, G., Lenci, S.: Identifying, evaluating, and controlling dynamical integrity measures in nonlinear mechanical oscillators. Nonlinear Anal. Theory Methods Appl. 63, 902–914 (2005)
Rega, G., Lenci, S.: A global dynamics perspective for system safety from macro- to nanomechanics: Analysis, control, and design engineering. Appl. Mech. Rev. 67, 050802 (2015)
Thompson, J.M.T.: Dynamical integrity: three decades of progress from macro to nano mechanics. In: Lenci, S., Rega, G. (eds.) Global Nonlinear Dynamics for Engineering Design and System Safety, pp. 1–26. Springer, Cham (2019)
Rega, G., Lenci, S., Ruzziconi, L.: Dynamical integrity: a novel paradigm for evaluating load carrying capacity. In: Lenci, S., Rega, G. (eds.) Global Nonlinear Dynamics for Engineering Design and System Safety, pp. 27–112. Springer, Cham (2019)
Settimi, V., Rega, G.: Local versus global dynamics and control of an AFM model in a safety perspective. In: Lenci, S., Rega, G. (eds.) Global Nonlinear Dynamics for Engineering Design and System Safety, pp. 229–286. Springer, Cham (2019)
Soliman, M.S., Thompson, J.M.T.: Integrity measures quantifying the erosion of smooth and fractal basins of attraction. J. Sound Vib. 135, 453–475 (1989)
Daeichin, M., Ozdogan, M., Towfighian, S., Miles, R.: Dynamic response of a tunable MEMS accelerometer based on repulsive force. Sens. Actuator A Phys. 289, 34–43 (2018)
Lyu, M., Zhao, J., Kacem, N., Liu, P., Tang, B., Xiong, Z., Wang, H., Huang, Y.: Exploiting nonlinearity to enhance the sensitivity of mode-localized mass sensor based on electrostatically coupled MEMS resonators. Int. J. Non-Linear Mech. 121, 103455 (2020)
HaLevy, O., Krakover, N., Krylov, S.: Feasibility study of a resonant accelerometer with bistable electrostatically actuated cantilever as a sensing element. Int. J. Non-Linear Mech. 118, 103255 (2020)
Masri, K.M., Younis, M.I.: Investigation of the dynamics of a clamped–clamped microbeam near symmetric higher order modes using partial electrodes. Int. J. Dyn. Control 3, 173–182 (2015)
Sun, K., Liu, L., Qiu, J., Feng, G.: Fuzzy adaptive finite-time fault-tolerant control for strict-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. (2020). https://doi.org/10.1109/TFUZZ.2020.2965890
Sun, K., Jianbin, Q., Karimi, H.R., Fu, Y.: Event-triggered robust fuzzy adaptive finite-time control of nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. (2020). https://doi.org/10.1109/TFUZZ.2020.2979129
Sun, K., Qiu, J., Karimi, H.R., Gao, H.: A novel finite-time control for nonstrict feedback saturated nonlinear systems with tracking error constraint. IEEE Trans. Syst. Man Cybern. Syst. (2019). https://doi.org/10.1109/TSMC.2019.2958072
Pu, D., Wei, X., Xu, L., Jiang, Z., Huan, R.: Synchronization of electrically coupled micromechanical oscillators with a frequency ratio of 3:1. Appl. Phys. Lett. 112(1), 013503 (2018)
Baguet, S., Nguyen, V.N., Grenat, C., Lamarque, C.-H., Dufour, R.: Nonlinear dynamics of micromechanical resonator arrays for mass sensing. Nonlinear Dyn. 95(2), 1203–1220 (2019)
Saghir, S., Bellaredj, M.L., Ramini, A.H., Younis, M.I.: Initially curved microplates under electrostatic actuation: Theory and experiment. J. Micromech. Microeng. 26(9), 095004 (2016)
Piccirillo, A., Gobbi, A.L.: Physical electrical properties of silicon nitride deposited by PECVD on III–V semiconductors. J. Electrochem. Soc. 137(12), 3910–3917 (1990)
Younis, M.I., Abdel-Rahman, E.M., Nayfeh, A.: A reduced-order model for electrically actuated microbeam-based MEMS. J. Microelectromech. Syst. 12(5), 672–680 (2003)
Ruzziconi, L., Bataineh, A.M., Younis, M.I., Cui, W., Lenci, S.: Nonlinear dynamics of an electrically actuated imperfect microbeam resonator: Experimental investigation and reduced-order modeling. J. Micromech. Microeng. 23(7), 075012 (2013)
Acknowledgements
The work has been developed during the visit of Laura Ruzziconi to King Abdullah University of Science and Technology (KAUST), Saudi Arabia; the kind hospitality is gratefully acknowledged. Nizar Jaber acknowledges support of King Fahd University of Petroleum and Minerals. This work is supported through KAUST Funds.
Author information
Authors and Affiliations
Contributions
LR developed the analysis of the experimental data and performed the theoretical investigation, NJ and LK acquired the experimental data, MLB fabricated the MEMS device, and MIY supervised the project. The present study is developed by a continuous and synergic collaboration among all authors. All authors read, revised, and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Problem formulation
Appendix 1: Problem formulation
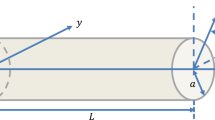
The device is modeled as a parallel plate capacitor, as represented in the schematic in Fig. 18. The microbeam is described in the framework of the Euler–Bernoulli theory. Axial and transversal displacements are denoted as w(z, t) and v(z, t), respectively. Along the vertical axis, we consider as positive direction the one toward the substrate. The microbeam is assumed of length L, width b, and thickness h (sum of all its layers). It is characterized by a straight configuration, constant rectangular cross section, and fixed–fixed boundary conditions. Residual stresses are represented by a constant axial load P, which induces axial displacement at the right end B. Since the lower electrode spans half the length of the microbeam, only this part contributes to the electric force term.
The governing equation of motion becomes [1]
where
and the electric force term is
where \(U\left({z}_{1}\right)\) and \(U\left({z}_{2}\right)\) are the unit step functions defining the lower electrode length and position. The boundary conditions are
In Eqs. (A.1)–(A.4), primes denote derivatives with respect to z, and dots denote derivatives with respect to t. The nondimensional variables are (denoted by tilde signs, which are dropped in (A.1)–(A.4) for convenience)
and the nondimensional parameters are
where EA is the axial stiffness, EJ is the bending stiffness, A is the area of the cross section, J is its moment of inertia, E is the effective Young’s modulus, ρ is the material density, d is the equivalent capacitor gap distance between the stationary electrode and the movable one, Ac is the overlapping area between the lower and the upper electrode (half-electrode configuration), c is the viscous damping coefficient, wB is the axial displacement at the right end B, ε0 is the dielectric constant in the free space, and εr is the relative permittivity of the gap space medium with respect to the free space.
The nondimensional axial force n and the time T are identified by referring to the linear part of Eq. (A.1) and matching the first two natural frequencies, which yields n = -145.5 (traction), and T = 0.0000513797.
Assuming these values, the first seven theoretical natural frequencies are estimated as: f1 = 145.2 kHz (first symmetric), f2 = 315.132 kHz (first antisymmetric), f3 = 526.637 kHz (second symmetric), f4 = 788.747 kHz (second antisymmetric), f5 = 1106.05 kHz (third symmetric), f6 = 1480.95 kHz (third antisymmetric), f7 = 1914.77 kHz (fourth symmetric). Up to f5, the theoretical values are very close to the experimental ones. This is even though the identification is conducted using only the first two natural frequencies.
Regarding the gap, the upper electrode is constituted by the conductive layer of gold/chrome applied on top of the microbeam; the silicon nitride (Si3N4), instead, is a dielectric material. For this reason, we consider the equivalent capacitor gap [67], which is composed of the air gap plus the contribution due to the silicon nitride layer, whose dielectric constant is \({\varepsilon }_{{\mathrm{rSi}}_{3}{\mathrm{N}}_{4}}\) = 7 [68]. Thus, the equivalent capacitor gap is
Regarding the parameter ka, this is evaluated by assuming the microbeam of homogeneous isotropic material (silicon nitride) and by referring to the equivalent capacitor gap, which yields ka = 28.868. For the parameter γ, we assume γ = 0.08; this value is slightly higher than the one extracted by matching the distance between the resonant and non-resonant branch of the principal attractors; this allows better observing the underlying phenomena. For the damping, we assume \(\xi \) = 0.053; also this value is slightly more elevated than the one extracted by matching (as far as possible) the lengthening of the principal resonant branch at small \({V}_{\text{AC}}\). This increment is deliberately added since calculating the attractor-basins phase portraits is computationally very demanding, and the higher damping facilitates the convergence of the trajectories to the corresponding attractors.
To derive the reduced-order model, we approximate the microbeam deflection as \(v(z, t)\cong {\sum }_{i=1}^{n}{\phi }_{i}(z){u}_{i}(t)\), where \({\phi }_{i}(z)\) are the corresponding mode shapes, normalized as \({\int }_{0}^{1}{\phi }_{i}{\phi }_{j}{\mathrm{d}}z={\delta }_{ij}\). Considering the third and fifth modes and applying the Galerkin method [69, 70], the 2 d.o.f. Galerkin reduced-order model becomes
where the first equation (n = 1) refers to the third mode and the second (n = 2) to the fifth. The electric force term is integrated numerically. The obtained coefficients are reported in Table 2.
Rights and permissions
About this article
Cite this article
Ruzziconi, L., Jaber, N., Kosuru, L. et al. Internal resonance in the higher-order modes of a MEMS beam: experiments and global analysis. Nonlinear Dyn 103, 2197–2226 (2021). https://doi.org/10.1007/s11071-021-06273-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06273-x