Dynamics and control of COVID-19 pandemic with nonlinear incidence rates

Abstract

World Health Organization (WHO) has declared COVID-19 a pandemic on March 11, 2020. As of May 23, 2020, according to WHO, there are 213 countries, areas or territories with COVID-19 positive cases. To effectively address this situation, it is imperative to have a clear understanding of the COVID-19 transmission dynamics and to concoct efficient control measures to mitigate/contain the spread. In this work, the COVID-19 dynamics is modelled using susceptible–exposed–infectious–removed model with a nonlinear incidence rate. In order to control the transmission, the coefficient of nonlinear incidence function is adopted as the Governmental control input. To adequately understand the COVID-19 dynamics, bifurcation analysis is performed and the effect of varying reproduction number on the COVID-19 transmission is studied. The inadequacy of an open-loop approach in controlling the disease spread is validated via numerical simulations and a robust closed-loop control methodology using sliding mode control is also presented. The proposed SMC strategy could bring the basic reproduction number closer to 1 from an initial value of 2.5, thus limiting the exposed and infected individuals to a controllable threshold value. The model and the proposed control strategy are then compared with real-time data in order to verify its efficacy.

1 Introduction

COVID-19, a novel coronavirus, caused an outbreak of atypical pneumonia first in Wuhan, Hubei province, China, in December 2019 and then rapidly spread out to the whole world. As per World Health Organization (WHO), as of May 23, 2020, globally, there are 5,105,881 confirmed cases and 333,446 deaths [1]. The whole world is in a lockdown scenario, having widespread socio-economic-political impacts. In this context, a study on the dynamics and possible control strategies could be of great interest to the research community and society as a whole.

Compared with statistics methods, mathematical modelling based on dynamical equations has received relatively less attention, though they can provide more detailed mechanism for the epidemic dynamics. The study of dynamics of epidemics started from 1760 by modelling smallpox dynamics, and since then, it has become an important tool in understanding the transmission and control of infectious diseases [2]. A watershed moment in the mathematical modelling and analysis of epidemic dynamics was the introduction of susceptible–infectious–removed (SIR) compartmental modelling approach to study the plague dynamics in India [3]. Since then, various compartmental modelling approaches have been used to study and understand the dynamics of infectious diseases.

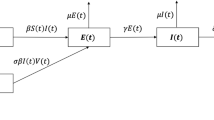
The classical SIR compartmental model divides total host population into three compartments/classes: S(t), I(t), and R(t), indicating fraction of population susceptible to infection, infected individuals, and removed individuals (either recovered or dead), respectively [4]. However, for most of the infectious diseases, a latent state exists before the individuals to pass from the infected to the infective state. This called for the introduction of an additional compartment, E(t), called exposed stage, making the system a four-dimensional ordinary differential equation (ODE) structure, called susceptible–exposed–infectious–removed (SEIR) model [5]. SEIR has been effectively used to understand the early dynamics of COVID-19 outbreak and to study the effectiveness of various measures since the outbreak [6,7,8,9,10]. In [8, 9], the COVID-19 dynamics was further generalised by introducing further sub-compartments, viz. quarantined and unquarantined, and the effect of the same on transmission dynamics was presented. In [11], the classical SEIR model was further extended to introduce delays to incorporate the incubation period in COVID-19 dynamics.

The mechanics of transmission of an epidemic is governed by the factor called incidence rate or force of infection. The incidence rate is generally represented as a linear function of infectious class, by principle of mass action, $\beta (I) = \beta _0I$, where $\beta (I)$ represents the incidence rate and $\beta _0$ represents the per capita contact rate [12]. But, like most of the real-life processes, it is more fitting to represent the incident rate using a nonlinear function. In a first, Capasso and Serio [13] used saturated incidence rate to model cholera transmission. Since then, nonlinear incidence rate functions of multiple forms have been used in the literature for modelling the disease spread rate [14]. In order to represent the nonlinear incident rate of the COVID-19 outbreak, the following function is used in this work [14].

$$\begin{aligned} \beta (I) = \frac{\beta _0I}{1+\alpha I^2}. \end{aligned}$$

(1)

Fig. 1

Variation of COVID-19 incidence rate function for different values of control variable, $\alpha$

In Eq. (1), the term $\beta _0I$ represents the bilinear force of infection and the term $1+\alpha I^2$ represents the inhibition effect, usually interpreted as the ‘psychological’ effect. This psychological effect is usually forced via aggressive Governmental measures, represented by $\alpha$, like isolation, quarantine, restriction of public movement, aggressive sanitation, etc. [15]. For lower values of infection, the public perception of the situation could be trivial, and this could increase the rate of infection rapidly. As more and more people around get infected, the public would start acknowledging the seriousness of the issue and could start responding positively to protection measures. The term ‘psychological’ effect is emphasised here due to the behavioural change of the susceptible public when the number of infective individuals is on the rise. This behavioural change could be via protective measures followed by susceptible individuals, viz. social distancing, sanitation, self-isolation, masks, etc. This public psychology is represented as a non-monotonous function, $\beta (I)$, as presented in Eq. (1). In this work, $\alpha$ is represented as the percentage of total effort required to contain/mitigate the epidemic spread.

Figure 1 presents the variation of incidence rate function for different values of the (Government) control variable, $\alpha$. For $\alpha >0$, in the presence of certain level of Governmental control to curb the spread, the incidence rate tends to fall after reaching a peak value. The absence of any Governmental control ($\alpha =0$) could cause infections to rise till the whole population is infected. It is interesting to note that for $\alpha =0$, $\beta (I) = \beta _0I$, representing a bilinear incidence rate.

This work attempts to analyse the dynamics of COVID-19 outbreak using the SEIR model, with nonlinear incident rate, with the help of bifurcation theory. In order to characterise the COVID-19 pandemic, the model parameters are adapted from the related literature [16,17,18,19,20,21]. Conditions are derived in terms of parameters for the existence of disease-free and endemic equilibrium points, and existence of a forward bifurcation point is presented. For different values of the Government control parameter $\alpha$, the intensity of outbreak is analysed. It was found that rather than having a random open-loop $\alpha$ selection, a closed-loop approach in controlling the COVID-19 spread would be more preferred. Motivated from this, this paper also presents a model-based closed-loop solution to control COVID-19 pandemic by the synthesis of appropriate threshold on Government control variable $\alpha$, using the technique of sliding mode control (SMC).

SMC has been widely used in the literature for the control of infectious diseases [22,23,24,25]. In [24], an influenza prevention method has been presented via robust vaccination and antiviral treatment using robust SMC , which could reduce the number of people susceptible to the virus. Again, in [22], using vaccination as a control input, an adaptive SMC was designed for controlling SEIR epidemic models . In [25], by forcing a threshold on the infection levels, a piecewise incidence rate, achieved using SMC, was used to control epidemic outbreaks. A similar approach was presented in [23], but the threshold value was forced on the number of exposed individuals. In the current context of COVID-19 pandemic, the authors attempt to utilise SMC to find an efficacious closed-loop control solution to prevent disease spread by synthesising appropriate control via Government action. A reaching law-based robust SMC design is adopted for control law synthesis, which could effectively control the transmission dynamics of COVID-19 epidemic even in the presence of external unanticipated disturbances and/or modelling uncertainties. The controller is designed in such a way that the exposed population dynamics has been controlled to a lower threshold, thereby actively controlling the mass spread of COVID-19.

Hence, the main objectives of this paper can be listed as follows:

• To analyse the COVID-19 dynamics via bifurcation theory for an in-depth understanding of the transmission dynamics and to study various factors that could aggravate/mitigate COVID-19 spread.

• To design a model-based closed-loop control solution for curtailing the disease spread to a manageable level using SMC.

The paper is organised as follows. The SEIR model and the dynamic analysis of the same are presented in Sect. 2. Section 3 describes the COVID-19 dynamics in detail using bifurcation analysis and establishes the significance of Governmental control action parameter, $\alpha$. SMC design for controlling the COVID-19 outbreak and associated results and discussions are presented in Sect. 4. Section 5 concludes the paper.

2 SEIR model and dynamic analysis

The basic SEIR model is given as,

$$\begin{aligned} \begin{aligned} {\dot{S}}&= \mu -\frac{\beta _0SI}{1+\alpha I^2}-\mu S,\\ {\dot{E}}&= \frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E,\\ {\dot{I}}&= \sigma E-(\gamma +\mu )I,\\ {\dot{R}}&= \gamma I-\mu R, \end{aligned} \end{aligned}$$

(2)

where the state variables [S, E, I, R] are the fractions of total population representing susceptible, exposed, infected, and removed, respectively. Birth/death rate is represented by $\mu$, and $\gamma$ represents the recovery rate. Parameter $\sigma$ is the measure of rate at which the exposed individuals become infected; in other words, $1/\sigma$ represents the mean latent period. The nonlinear incidence rate, presented in Eq. (1), is used in the model.

For the set of equations presented in Eq. (2), it is possible to write,

$$\begin{aligned} \varSigma =\{(S,E,I,R)\in \mathfrak {R}^{4}_{+}~:~S+E+I+R=1\}. \end{aligned}$$

(3)

Since $\varSigma$ is positively invariant and $R=1-(S+E+I)$, one could reduce the order of Eq. (2) by neglecting ${\dot{R}}$ dynamics, and the new set of equations can be presented as,

$$\begin{aligned} \begin{aligned} {\dot{S}}&= \mu -\frac{\beta _0SI}{1+\alpha I^2}-\mu S,\\ {\dot{E}}&= \frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E,\\ {\dot{I}}&= \sigma E-(\gamma +\mu )I.\\ \end{aligned} \end{aligned}$$

(4)

Also, by comparing Eqs. (2) and (4), one could notice that

$$\begin{aligned} {\dot{S}}+{\dot{E}}+{\dot{I}}= & {} \mu -\mu S-\mu E-(\gamma +\mu )I\nonumber \\\le & {} \mu -\mu (S+E+I), \end{aligned}$$

(5)

indicating the fact that $\lim _{t\rightarrow \infty } (S+E+I)\le 1$ and the feasible region for Eq. (4) can be represented as,

$$\begin{aligned} \varGamma =\{(S,E,I)\in \mathfrak {R}^{3}_{+}~:~0\le S+E+I\le 1\}. \end{aligned}$$

(6)

The most important threshold that determines the disease spread is the basic reproduction number, $R_0$. This value points to the number of secondary infections an infected individual would produce in a susceptible population. In order to find $R_0$, one needs to find the Jacobian of Eq. (4) about its disease-free equilibrium point, $E^*_{DFE}$, which can be calculated by equating Eq. (4) to zero and solving for $I^*=0$. The disease-free equilibrium for Eq. (4) is given by $E^*_{DFE}=(1,0,0)$. Now the Jacobian matrix for Eq. (4) is given by,

$$\begin{aligned}&J(S,E,I)\nonumber \\&\quad = \begin{bmatrix} -\mu &{} 0 &{} \frac{-(1+\alpha I^2)\beta _0S-\beta _0S(2\alpha I)}{(1+\alpha I^2)^2}\\ \frac{\beta _0I}{1+\alpha I^2} &{} -(\mu +\sigma ) &{} \frac{(1+\alpha I^2)\beta _0S-\beta _0S(2\alpha I)}{(1+\alpha I^2)^2}\\ 0 &{} \sigma &{} -(\mu +\gamma ) \end{bmatrix}. \end{aligned}$$

(7)

Now, to find $R_0$, the characteristic equation $|\lambda I-J|=0$ at $E^*_{DFE}$ is derived and is given as,

$$\begin{aligned}&(\lambda +\mu )\left[ \lambda ^2+(2\mu +\gamma +\sigma )\lambda \right. \nonumber \\&\quad \left. +(\mu +\sigma )(\mu +\gamma )-\sigma \beta _0 \right] =0. \end{aligned}$$

(8)

Since $E^*_{DFE}$ is stable, all the coefficients of Eq. (8) should be positive and all roots should have negative real parts. This implies

$$\begin{aligned} (\mu +\sigma )(\mu +\gamma )-\sigma \beta _0 >0, \end{aligned}$$

(9)

and the basic reproduction number $R_0$ is given by,

$$\begin{aligned} R_0 = \frac{\sigma \beta _0}{(\mu +\sigma )(\mu +\gamma )}. \end{aligned}$$

(10)

Theorem 1

For the system represented by Eq. (4) with positive parameters, $E^*_{DFE}=(1,0,0)$ is locally stable if $R_0$$<1$ and unstable in $R_0$$>1$.

Proof

From Eq. (8), the characteristic equation can be written as,

$$\begin{aligned} s&(\lambda +\mu )\left[ \lambda ^2+(2\mu +\gamma +\sigma )\lambda \right. \nonumber \\&\quad \left. + (\mu +\sigma )(\mu +\gamma )(1-R_0) \right] =0. \end{aligned}$$

(11)

If $R_0<1$, all the coefficients of the characteristic equation are positive and all three eigenvalues are negative, indicating a stable equilibrium. For $R_0$$>1$, there exist a positive eigenvalue for Eq. (11) and the equilibrium solution in unstable. $\square$

Theorem 2

For the system represented by Eq. (4) with positive parameters, there exist an endemic equilibrium ($S^*,E^*,I^*$) for $R_0$$> 1$ and no unique endemic equilibrium for $R_0$$< 1$.

Proof

To find the endemic equilibrium ($S^*,E^*,I^*$), system presented in Eq. (4) is equated to zero,

$$\begin{aligned}&\mu -\frac{\beta _0S^{*}I^{*}}{1+\alpha I^{*2}}-\mu S^*=0, \end{aligned}$$

(12a)

$$\begin{aligned}&\frac{\beta _0S^{*}I^{*}}{1+\alpha I^{*2}}-(\sigma +\mu )E^{*}=0, \end{aligned}$$

(12b)

$$\begin{aligned}&\sigma E^{*}-(\gamma +\mu )I^{*}=0. \end{aligned}$$

(12c)

Now, from Eq. (12c),

$$\begin{aligned} E^* = \frac{(\gamma +\mu )I^*}{\sigma }. \end{aligned}$$

(13)

Substituting $E^*$ in Eq. (12b), we obtain

$$\begin{aligned}&\frac{\beta _0S^{*}I^{*}}{1+\alpha I^{*2}}-(\sigma +\mu )\left( \frac{(\gamma +\mu )I^{*}}{\sigma }\right) =0.\\&\frac{\beta _0S^{*}I^{*}}{1+\alpha I^{*2}}=\frac{(\sigma +\mu )(\gamma +\mu )I^{*}}{\sigma }.\\&S^{*}=\frac{(\sigma +\mu )(\gamma +\mu )}{\beta _0\sigma }(1+\alpha I^{*2}). \end{aligned}$$

Now, $S^*$ can be represented in terms of basic reproduction number as,

$$\begin{aligned} S^*=\frac{1+\alpha I^{*2}}{R_0}. \end{aligned}$$

(14)

Substituting Eqs. (13) and (14) in Eq. (12a), one could find $I^*$ as the positive solution of

$$\begin{aligned} \varTheta ={\mathscr {A}}I^{*2}+{\mathscr {B}}I^*+{\mathscr {C}} = 0, \end{aligned}$$

where

$$\begin{aligned} {\mathscr {A}} = \frac{\mu \alpha }{R_0}, {\mathscr {B}} = \frac{\beta _0}{R_0}, {\mathscr {C}} = \left( \frac{1}{R_0}-1\right) \mu . \end{aligned}$$

It is clear that ${\mathscr {A}}>0$ and ${\mathscr {B}}>0$. For $R_0>1$, ${\mathscr {C}}<0$, and there exist a positive solution for $\varTheta$ and hence a unique endemic equilibrium. For $R_0<1$, ${\mathscr {C}}>0$ and there exist no endemic equilibrium for this condition. Theorems 1 and 2 have been formulated following a similar trend as in the literature [12, 13].

Next, the equilibria analysis presented above is corroborated by performing the bifurcation analysis of the SEIR model presented in Eq. (2). For the sake of completeness, the coming section presents a short introduction to the bifurcation and procedure adopted.

3 Bifurcation and continuation analysis

To study the dynamics of parameterised nonlinear dynamical systems, bifurcation analysis and continuation theory methodology has emerged as one of the most efficient tools. It is possible to compute all possible steady states of the nonlinear model as function of a bifurcation parameter along with local stability information of the steady states. The qualitative global dynamics are usually represented using bifurcation diagrams. Bifurcation diagrams are usually generated with the help of numerical continuation algorithms, such as AUTO [26]. In order to perform the bifurcation analysis, the nonlinear systems are usually described by set of nonlinear ordinary differential equations of the form [27]:

$$\begin{aligned} \dot{\underline{{\mathscr {X}}}}=\underline{{\mathscr {F}}}(\underline{{\mathscr {X}}}, \underline{{\mathscr {U}}}), \end{aligned}$$

(15)

where $\underline{{\mathscr {X}}}$ and $\underline{{\mathscr {U}}}$ are the state vector ($\underline{{\mathscr {X}}} \in \mathfrak {R}^n$) and the control vector ($\underline{{\mathscr {U}}} \in \mathfrak {R}^m$), respectively, and function $\underline{{\mathscr {F}}}(\underline{{\mathscr {X}}},\underline{{\mathscr {U}}})$ defines the mapping such that $\mathfrak {R}^n \times \mathfrak {R}^m \rightarrow \mathfrak {R}^n$.

In a first, one parameter is chosen to be varying stepwise, called bifurcation parameter, fixing other parameters to their constant values. Fixed points are computed at each step by solving

$$\begin{aligned} \dot{\underline{{\mathscr {X}}}}^{*}=\underline{{\mathscr {F}}} (\underline{{\mathscr {X}}}^{*},u^{*},\underline{{\mathscr {P}}}^{*})=0, \end{aligned}$$

(16)

where $u\in \underline{{\mathscr {U}}}$ and $\underline{{\mathscr {P}}}\in \underline{{\mathscr {U}}}$ represent the bifurcation parameter and the set of fixed parameters, respectively. Once a fixed point ($(\underline{{\mathscr {X}}}^*,~u^*)$) is known, in a continuation, the next point $(\underline{{\mathscr {X}}}_1,u_1)$ is predicted by solving:

$$\begin{aligned} \frac{\partial \underline{{\mathscr {F}}}}{\partial \underline{{\mathscr {X}}}}|_{(\underline{{\mathscr {X}}}^*,~u^*)}\varDelta \underline{{\mathscr {X}}}+\frac{\partial \underline{{\mathscr {F}}}}{\partial u}|_{(\underline{{\mathscr {X}}}^*,~u^*)}\varDelta u=0. \end{aligned}$$

(17)

These predicted values are then corrected to satisfy Eq. (16) to get the next fixed point $(\underline{{\mathscr {X}}}^{*}_{1},u_1)$. Along with computation of new fixed points, in a continuation, it is possible to determine their stability based on the eigenvalues of the Jacobian matrix. While plotting the bifurcation curve, this stability information is also included.

Fig. 2

Bifurcation diagram of $E^*$ and $I^*$ versus $R_0$—for $\mu =0.1$, $\sigma = 1/7$, $\gamma = 1/5$ (solid lines—stable trims; dashed lines—unstable trims)

Table 1 Summary table of the COVID-19 parameters

For the problem at hand, the basic reproduction number $R_0$ is chosen as the bifurcation parameter to perform the analysis. From the above analysis, it is clear that the bifurcation point for the model considered is at $R_0=1$. The bifurcation plots presented in Fig. 2 also corroborate this point. In order to conduct the analysis, the parameter values corresponding to COVID-19 are adapted from the literature [16, 18,19,20,21]. There is a significant change in the system behaviour at this point. The disease-free and endemic equilibrium behaves differently before and after $R_0=1$. For $R_0<1$, the disease-free equilibrium point is stable and endemic equilibrium point is unstable for all values of $R_0$. As $R_0$ increases and crosses 1, the disease-free equilibrium losses its stability and a stable equilibrium solution branch emerges, indicating endemic equilibrium solutions.

Fig. 3

Numerical simulation results showing endemic equilibrium at $R_0=1.7$

Bifurcation results are used to anticipate the qualitative behaviour associated with a nonlinear dynamical system. Supplementing the bifurcation plots with numerical simulation results are often recommended/demanded. In this regard, in this paper, sets of numerical simulation results are presented for different conditions. The dynamics associated with $R_0<1$ is of less interest due to the existence of the disease-free equilibrium point. Higher $R_0$ values indicate larger force of infection and spread, and the curves could reach its equilibrium values in shorter time. For COVID-19 pandemic, the actual $R_0$ estimate lies between 1.5 and 3.5 [17], and to show the dynamics of stable steady-state endemic equilibrium solution branch, a basic reproduction number value of $R_0=1.7$ (near the lower estimate value) is selected. Assuming the outbreak is occurring in a city with 5 million population, with 90% of the people susceptible to COVID-19 disease and 500 people having exposed to the virus, the initial condition can be written as ${\mathscr {X}}(0) = (S(0),E(0),I(0),R(0))=(0.9,0.0001,0,0)$. A set of parameters used for the analysis is presented in Table 1.

Figure 3 shows the evolution of number of people getting exposed, infected and finally recovered/removed due to COVID-19 for $R_0=1.7$. From 500 exposed individuals, with in a span of 60 days, 0.63 million people got infected and approximately double the number, and 1.22 million people got newly exposed to the COVID-19 virus. This can be verified from the bifurcation diagram presented in Fig. (2) by multiplying the ($E^*, I^*$) equilibrium values with total population.

Fig. 4

Numerical simulation results showing evolution of infected population as a fraction of total population for different values of $R_0$

Fig. 5

Numerical simulation results with Government control action ($\alpha \ne 0$) for $R_0=2.5$

Figure 4 presents the time evolution of infected population fraction for different values of $R_0$. From [17], the range of $R_0$ for COVID-19 was found to be between 1.5 and 3.5 and same range is chosen here. There is a significant variation in the number of days taken for the infection to peak to its equilibrium value. The line connecting the markers represents the locus of the equilibrium points for different values of $R_0$ and appears almost linear. For $R_0=1.5, 2, 2.5,~\text {and}~3.5$, the number of days for the infection curve to peak is 70, 49, 35 and 22, respectively. So, by using bifurcation data, it is possible to have a rough estimate of what to expect during an outbreak.

One should note that the plots presented above are for $\alpha =0$, indicating no Government intervention. But this would not be the actual case. Governments all around the world are working hard to control and mitigate COVID-19 with different success rates. For the nonlinear incidence rate considered in this paper, as mentioned above, parameter $\alpha >0$ is modelled as the control parameter indicating Government action. The magnitude of $\alpha$ is modelled as an indication of how aggressive the intervention is. Physically, this could be viewed as the measures to reduce the COVID-19 transmission, by trying to arrest $R_0$ to a lower value. The more Government restrict the public interaction by forcing isolation, quarantine, masks, lockdown, etc., the faster the COVID-19 transmission slows down.

Figure 5 presents the effect of different values of $\alpha$ (introduced as a step change), indicating the aggressiveness of Government restriction/control in arresting the COVID-19 spread. The effectiveness/severity of Governmental control strategies is represented in percentages, with 100% being measures like complete lockdown with travel restrictions. There is a clear reduction in the number of exposed and infected cases as $\alpha$ increases. The total number of exposed cases and infected cases reduces drastically from 0.85 million and 0.44 million (for low Government control, such as advertisements, quarantining exposed people) to 0.3 million and 0.17 million (for much stringent control like lockdown), respectively. While studying the control scenarios, one should keep a keen eye on the value of $R_0$ to know the efficacy of the control steps. The plots presented in Fig. 5 are generated for $R_0=2.5$ for nonzero $\alpha$ values, selected at random. As $\alpha$ increases, due to the control measures, naturally $R_0$ should come down to a lower value, thus reducing the spread and making the epidemic controllable.

Fig. 6

Variation of $R_0$ with $\alpha$

The plot of $R_0$ with varying $\alpha$ is presented in Fig. 6. When control is introduced, there is a faster drop in $R_0$ even for smaller values of $\alpha$. As $\alpha$ becomes high, the restrictions become more and more stringent. One might consider to impose much higher restrictions thinking only about the initial pattern to control the COVID-19 spread and bring $R_0$ to a disease-free equilibrium point. But, from the studies, it was clear that the magnitude of drop in $R_0$ tends to saturate at higher $\alpha$ values, making the additional imposed restrictions useless.

Another important point to note is the arbitrariness in the selection of $\alpha$ value to have certain level of ‘open-loop control to arrest/mitigate the disease transmission by bringing down the $R_0$ value. Even though this method can reduce the COVID-19 transmission, the effectiveness of this method in bringing the transmission down to much smaller rates seemed unfeasible. Selection of $\alpha$ as a step input has its own limitations. Sudden introduction of control measures and sustaining the same for longer time periods might have a negative psychological impact on the public and could limit the success rate. If one can adopt a methodology to gradually introduce some relaxations to the public (as incentives) in the Government action ($\alpha$) with a specific target (like limiting the number of exposed/infected people to a smaller threshold value), that could serve as a better alternative to control a global pandemic like COVID-19. In this regard, a closed-loop control approach, using sliding mode technique, that would be capable of introducing control measures gradually depending up on instantaneous infection rates is being presented next.

4 Sliding mode control for COVID-19

Sliding mode control (SMC) is a model-based control solution, which has been found suitable for many physical systems. It is a form of variable structure control, in which the control law takes different structures for ensuring desired system dynamics [28]. In SMC design, the first step is to define a sliding surface that would characterise the desired dynamics to be achieved. The second step is the design of control laws that would essentially drive the system to reach and stay on the desired dynamics (sliding surface). Once the system reaches the sliding surface, it is said to be in sliding mode, in which the system would have robustness property.

Here, the attempt is to define a sliding surface in terms of the desired dynamics of the fraction of the exposed population (E) so as to control COVID-19 pandemic in a systematic manner. The sliding surface would be defined such that the exposed population asymptotically converges to a desired value. Making the Governmental action ($\alpha$) as the control input, the attempt here is to bring the exposed population dynamics to the desired dynamics (sliding surface) and make it to slide along the desired dynamics towards the desired value. The reasons to chose E as the controlled variable are the following:

• To avoid zero dynamics in the closed-loop system, choosing E as the controlled variable would result in a relative degree of 1, when $\alpha$ is the control input. This would eliminate zero dynamics and makes controller design straightforward.

• Variable E has a direct impact in the dynamics of infection and in turn the whole system.

Since the goal is to contain the COVID-19 transmission by bringing the $R_0$ value close or less than 1, the aforementioned desired exposed population value is directly selected from bifurcation diagram presented in Fig. 2 for a desired $R_0$ range.

4.1 Controller design

For controlling the state variable E to the desired value $E_d$, the sliding surface, $\varsigma$ is defined as:

$$\begin{aligned} \varsigma =\varLambda (E-E_{d})=0, \end{aligned}$$

(18)

where $\varLambda >0$ is the slope of the sliding surface, which determines the speed at which the system reaches the sliding surface. For designing the control law for reaching the sliding surface, the well-established constant rate reaching law (CRRL) technique has been used in this paper [29, 30]. CRRL is given by

$$\begin{aligned} {\dot{\varsigma }}=-\kappa \mathrm{sign}(\varsigma ), \end{aligned}$$

(19)

where $\kappa$ represents the controller gain in CRRL structure. To obtain the control law, we recall the following dynamic equation for exposed population:

$$\begin{aligned} {\dot{E}} = \frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E. \end{aligned}$$

(20)

Now using Eq. (18), the CRRL structure [Eq. (19)] can be realised as

$$\begin{aligned} \varLambda ({\dot{E}}-{\dot{E}}_{d})= -\kappa \mathrm{sign}(\varsigma ), \end{aligned}$$

(21)

Since $E_d$ is a constant value, which is the desired exposed population value from the bifurcation diagram, $\dot{E_{d}}\rightarrow 0.$ Now using Eq. (20), we obtain

$$\begin{aligned} \varLambda \Big ( \frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E\Big )=-\kappa \mathrm{sign}(\varsigma ), \end{aligned}$$

(22)

which gives the Governmental control action, $\alpha$ as,

$$\begin{aligned} \alpha =\frac{1}{I^2}\Bigg [\frac{\varLambda \beta _0SI}{-\kappa \mathrm{sign}(\varsigma )+\varLambda (\sigma +\mu )E} -1\Bigg ]. \end{aligned}$$

(23)

Depending upon the instantaneous deviation of E (based on Government test results) from the desired value, Eq. (23) provides the appropriate control action.

Physically, the interpretation of control action as presented by Eq. (23) can be explained in the following manner.

Rather than keeping the aggressive action plan/control same throughout the disease period (a constant $\alpha$), in the presented method, Government would have the flexibility to give certain level of relaxations like, allowing essential services/ restricted freedom of movement, etc., to the people. This in turn could create positive psychological impact among the people to comply to Government-imposed restrictions.

4.2 Stability analysis

In order to analyse the finite-time asymptotic convergence of E to the desired value using the CRRL-based SMC design, stability analysis using Lyapunov’s method is presented here [28]. For this, the Lyapunov function is chosen as

$$\begin{aligned} V=\frac{1}{2}\varsigma ^2. \end{aligned}$$

(24)

The condition for asymptotic stability with respect to the equilibrium point $\varsigma =0$ is that ${\dot{V}}<0 \>\> \forall \varsigma \ne 0$. Differentiating Eq. (24),

$$\begin{aligned} {\dot{V}}=\varsigma {\dot{\varsigma }}. \end{aligned}$$

(25)

For stability analysis, consider the presence of a bounded disturbance, $\epsilon$ in the dynamics of E, such that Eq. (20) is rewritten as

$$\begin{aligned} {\dot{E}} = \frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E+\epsilon . \end{aligned}$$

(26)

Using Eq. (18) and assuming $\varLambda =1$ for simplicity, Eq. (25) can be written as

$$\begin{aligned} {\dot{V}}=\varsigma {({\dot{E}}-{\dot{E}}_d)}, \end{aligned}$$

(27)

which gives [using Eq. (26)],

$$\begin{aligned} {\dot{V}}=\varsigma \Bigg (\frac{\beta _0SI}{1+\alpha I^2}-(\sigma +\mu )E+\epsilon -{\dot{E}}_d\Bigg ). \end{aligned}$$

(28)

Since $\dot{E_{d}}\rightarrow 0$ and on substituting the CRRL control structure, Eq. (23), in the above equation, we obtain

$$\begin{aligned} {\dot{V}}=\varsigma \epsilon -\varsigma \kappa \mathrm{sign}(\varsigma ). \end{aligned}$$

(29)

where $\kappa >0$. Assuming that the disturbance $\epsilon$ is limited by an upper bound $\phi$, then

$$\begin{aligned} {\dot{V}}<|\varsigma |\phi -\varsigma \kappa \mathrm{sign}(\varsigma ) \end{aligned}$$

(30)

which gives

$$\begin{aligned} {\dot{V}}<-|\varsigma |(\kappa -\phi ). \end{aligned}$$

(31)

To ensure that ${\dot{V}}<0 \>\> \forall ~\varsigma \ne 0$ (for Lyapunov stability),

$$\begin{aligned}&|\varsigma |(\kappa -\phi )>0 \>\> \forall \varsigma \ne 0, \end{aligned}$$

(32)

$$\begin{aligned}&\implies \kappa >\phi . \end{aligned}$$

(33)

This implies that, if the CRRL gain, $\kappa$ is selected based on the deterministic disturbance bound $\phi$, as per above inequality, then the closed-loop system can be asymptotically stable, driving E to $E_d$ in finite time.

Fig. 7

Numerical simulation results presenting uncontrolled and controlled dynamics of exposed and infected population

4.3 Results and discussion

In order to control the transmission of COVID-19 pandemic, the Governmental action is modelled by using Eq. (23) and the fraction of exposed population (E) is controlled to a lower value. To address the inherent chattering issue (high-frequency control signal switching in sliding mode) in SMC, saturation function is used instead of the signum function [28]. An initial $R_0$ value of 2.5 is chosen, resembling COVID-19 basic reproduction number. At this rate, if there is no Government control, as presented in Fig. 7a, b, then the total number of exposed and infect individuals could rise to 1.8 million (36% of total population) and 0.93 million (18.6% of total population), respectively in 30 days. The goal is to limit this outburst to a lesser controllable value with the help of Governmental control. To achieve this, the value of $E_d$ (limit on the number of exposed individuals) is chosen to be 1% of the total population. Other system parameters ($\mu =0.1,\sigma =1/7,\gamma =1/5$) are selected to replicate COVID-19 dynamics. Values of design parameters are selected as $\kappa =1$ and $\varLambda =1$. To check the robustness, it is assumed that, up on further Government inspection and testing, a cluster of individuals amounting to 0.1% of the total exposed population is found to be newly exposed to the disease, and this fraction is added as the external disturbance.

Fig. 8

Plots of time histories of Governmental control effort and variation in $R_0$ in order to limit the COVID-19 spread limit to that in Fig. 7c

Figure 7c, d presents the controlled dynamics of exposed and infected population. Using the appropriate Governmental control, it was possible to limit the total number of exposed and infected cases to 0.05 million and 0.026 million (1% and 0.52%), respectively. This is in sharp contrast with the scenario, where there is no actual control, as shown in Fig. 7a, b, highlighting the significance of the proposed method. With the aforementioned controller parameter values, this improvement is achieved in 40 days. This is accomplished using the Governmental action plan, as suggested in Fig. 8a.

In this work, the magnitude of $\alpha$, represented in percentages, could be considered as the Governmental effort to control the spread. Values ranging from $0\%$ to $100\%$ emphasise the intensity of the Governmental action in mitigating the COVID-19 spread. This could be via approaches like lockdown, nationwide testing, rampant awareness campaigns, travel restrictions, banning social and public gatherings, etc. The degree of restrictions limiting the spread is classified under different $\alpha$ brackets. For instance, a nationwide lockdown with blanket ban on all activities was given an $\alpha$ value of 100%. A much more relaxed approach allowing basic economic activities was assigned a value $\alpha \approx 75\%$, private travel along with basic economic activities and essential shops allotted an approximate $\alpha$ value of 50%, introduction of limited public transport classified into $\alpha \approx 25\%$, and much smaller values were designated for further relaxations.

To arrest a major outbreak, one should expect a certain level of aggressive Government action from the initial phase itself. This value could corresponds to steps like complete lockdown of the city, by banning all public gatherings, transportation services, public interactions, aggressive testing and mass forced home quarantines for all the exposed/infected individuals. But, keeping the Government control at this higher value through out the whole period could not work as well. A numerical simulation with $\alpha =100\%$ (much like open-loop analysis presented in Fig. 5) for the same set of initial conditions resulted in much higher number of exposed and infected cases, 0.18 million and 0.092 million, respectively. For the proposed closed-loop control strategy, this is not the case. Here, the Governmental control effort is adjusted according to the control objective, i.e. limiting the number of exposed cases to 1% of total population. So, as the goal is to keep the COVID-19 spread in check and to prevent a massive outbreak, this methodology serves its purpose. It is interesting to note that the proposed Governmental action plan curve resembles the real world COVID-19 control strategies adopted by countries like India and South Korea, where a massive outbreak was prevented. India, with a colossal 1.33 billion population, on the verge of a huge outbreak underwent a nationwide lockdown (with restrictions of varying degree similar to Fig. 8a) limiting the number of infected cases to approximately 0.011 million, which would have been around 0.82 million without this step [31]; meanwhile, South Korea did aggressive testing from the initial day itself and imposed quarantines for exposed/infected people (much like the initial phase of Fig. 8a), flattening the infection curve with in 30 days. Once the desired threshold is reached, then it is possible to phase out the spread in a much controlled manner. This is achieved by bringing the $R_0$ value down to a much controllable number. Starting from a value of 2.5, using the $\alpha$ profile presented in Fig. 8a, the basic reproduction number is brought down to a value of $R_0=1.01$ as presented in Fig. 8b. From this point, the spread is certainly under control and could be phased out carefully without the risk of further outbreak.

5 Comparison with real-time data

In order to validate the model and control strategy presented, the proposed dynamics is compared with real-time data. Data corresponding to India, a country who imposed strict Governmental measures to contain the COVID-19 pandemic, are compared here. Indian policies were similar to that of the proposed control strategy as presented in this paper. On March 25, India imposed a nationwide strict lockdown [32]. India had divided the lockdown, which is still continuing in the country (as on 23/05/2020) into four phases with varying degree of relaxations [33, 34]. The idea during phase I was to have a complete country lockdown [33], but the public perception was not up to the mark. The socio-economic-cultural factors of a huge country like India also reduced the effectiveness of a compete lockdown. Nonetheless, the country was saved from a massive outbreak due to the early and timely Government intervention in line with WHO guidelines [35]. The best fit $R_0$ estimate for India was found to be 2.083 before the lockdown initiation and currently (23/05/2020), the value hovers around $R_0\approx 1.226$ [36].

Fig. 9

Infected population evolution for India

Fig. 10

Plots of time histories of Governmental control effort and variation in $R_0$ in order to limit the COVID-19 spread limit to that in Fig. 9

Figure 9 presents the comparison between the COVID-19 transmission trend as suggested by the SEIR model with a nonlinear incidence rate function and real-time data for India [37]. Day 0 represents 25/03/2020, the day on which Government of India initiated nationwide lockdown with 657 infected cases [37]. The plan was to have a total ban on all activities across the country for 21 days. After 21 days, on 15/04/2020, second phase started for 19 days with varying relaxations like controlled interstate movement of people, depending on the number of active cases at different states. Third phase began on 04/05/2020 and ended on 17/05/2020 with increasing degree of relaxations including limited public transport, still maintaining social distancing. India is currently on the fourth phase, with most of the activities open all around the country, including air and train travel.

The infected population evolution as predicted by SEIR model [presented by Eq. (2)] closely resembles the real-time infection data as presented in Fig. 9. This is of great significance considering the complex dynamics (owing to diverse socio-economic-religious-political spheres with huge population unlike any other country) associated with Indian COVID-19 spread. The total number of infected people, in case of no Governmental control, as projected by SEIR model is also presented. The curves are presented in logarithmic scale for better presentation and comparison. SEIR model used in this work hypothesised a dreadful projection of 21.54 million infected persons on 23/04/2020 in absence of any Government intervention. The model is simulated to closely resemble the actual scenario. The reproductive number $R_0$ is brought down from an initial value of 2.083–1.226 (to resemble Indian scenario) using sliding mode controller. The control effort needed to do so is presented in Fig. 10a, and corresponding $R_0$ profile is shown in Fig. 10b.

Interestingly, if one were to compare the $\alpha$ plot with Indian Governmental control effort (assuming a distribution presented above), one could observe a similar trend. A representative class of Indian Governmental action plot is also presented in Fig. 10a. Even though the plot represents a rough estimation of Governmental effort, it is interesting to note a similar trend as suggested by the model-based control approach. The real-time Governmental action is based on data-based approaches, and this work shows a systematic model-based approach that can be used as a good alternative/supplement to aid in successfully mitigating the pandemic. One has to consider model-based predictions seriously for better control of the pandemic outbreak. These predictions are based on the dynamics and varies from time to time. It is imperative to update the predictions frequently based on the then model parameters and controlling measures have to be formulated differently. The control profiles from the sliding mode controller can act as a benchmark while devising COVID-19 control strategies. The proposed SEIR model with nonlinear incidence rate function can describe the COVID-19 dynamics with a certain degree of uncertainty.

6 Conclusions

Governments all over the world currently try to tackle COVID-19 pandemic in their own unique ways, with varying success rates. A systematic method for the analysis and control of COVID-19 dynamics is a need of the hour. In this context, a bifurcation theory-based analysis approach to comprehend the COVID-19 transmission dynamics has been presented. The Governmental control parameter $\alpha$ is introduced via a nonlinear incidence function, and both open-loop and closed-loop control strategies are attempted. Unlike the open-loop method, the closed-loop control solution via sliding mode control (SMC) allows to have an effective Governmental control over the situation depending upon the intensity of the infection. The proposed action plan is to have an aggressive containment plan during the initial phase of outbreak, bringing the basic reproduction number down to keep a tight rein on the COVID-19 transmission, then allowing some relaxations to increase the public confidence and phasing out the COVID-19 pandemic in a timely manner. Comparison of the SEIR model with Governmental control with real-time data revealed similar trend, indicating the adequacy of proposed methodology in representing the COVID-19 dynamics.