Modeling tangential friction based on contact pressure distribution for predicting dynamic responses of bolted joint structures

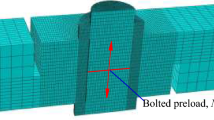
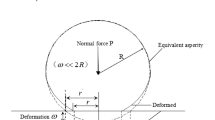
Abstract

Subjected to dynamic excitations, bolted joint interfaces exhibit nonlinear characteristics that significantly affect the dynamic response of assembled structures. In this paper, a novel modeling method is developed to improve the prediction accuracy of the tangential contact behavior of bolted joint interfaces. This method is based on the framework of the Iwan model and builds the relationship between the Iwan density function and the distribution of the contact pressure. It is the first time to give an explicit physical significance of the Iwan density function. The effectiveness of the proposed model is validated well by comparing with published experiments. Then the proposed model is integrated into a numerical model of a bolted joint structure and combined with the alternating frequency/time method to study its applicability in dynamics analysis. The model is fully compatible with the current state-of-the-art numerical analysis tools. The results show that the simulated interface responses are in good agreement with the experiment.

Appendices

Appendix A: Contact parameters and imposed displacements in the quasi-static tests

See Table 1.

Table 1 Maximum imposed displacements and contact parameters (friction coefficient and contact stiffness) for different preload levels

Appendix B: Model parameters of the bolted joint oscillator

See Table 2.

Table 2 Model parameters of the bolted joint oscillator

Appendix C: Nonlinear dynamic response simulation

The MHBM is used to approximate dynamic response through Fourier series. Taking the displacement response, as an example, the real solution can be expanded into a series of harmonic components,

$$ \varvec{u} = \varvec{U}_{\varvec{o}} + \sum_{j = 1}^{{n_{h} }} \left[ {\varvec{U}_{\varvec{j}}^{\varvec{c}} \cos \left( {j\omega t} \right) + \varvec{U}_{\varvec{j}}^{\varvec{s}} \sin \left( {j\omega t} \right)} \right], $$

(C1)

where $\varvec{U}_{\varvec{j}}^{\varvec{c}}$ and $\varvec{U}_{\varvec{j}}^{\varvec{s}}$ are the sinusoidal and cosinoidal harmonic coefficients, $\varvec{U}_{\varvec{o}}$ the constant component of displacement individually, $j$ the order of Fourier series, $n_{h}$ the truncated order of harmonics and $\omega$ the principal vibration frequency. Similarly, the vectors of nonlinear force and excitation force can also be approximated in the same way,

$$ \varvec{F}_{\varvec{e}} = \varvec{F}_{\varvec{o}} + \sum_{j = 1}^{{n_{h} }} \left[ {\varvec{F}_{\varvec{j}}^{\varvec{c}} \cos \left( {j\omega t} \right) + \varvec{F}_{\varvec{j}}^{\varvec{s}} \sin \left( {j\omega t} \right)} \right], $$

(C2)

$$ \varvec{f}_{{\varvec{nl}}} = \varvec{f}_{\varvec{o}} + \sum_{j = 1}^{{n_{h} }} \left[ {\varvec{f}_{\varvec{j}}^{\varvec{c}} \cos \left( {j\omega t} \right) + \varvec{f}_{\varvec{j}}^{\varvec{s}} \sin \left( {j\omega t} \right)} \right]. $$

(C3)

The vibration differential equation, Eq. (15), can be transformed to an algebraic form,

$$ \varvec{Z}\left(\varvec{\omega}\right)\varvec{u} = \varvec{F}_{\varvec{e}} - \varvec{f}_{{\varvec{nl}}} , $$

(C4)

where $Z\left( \omega \right)$ is the dynamic stiffness matrix which represents the linear part of the system and can be defined as,

$$ \varvec{Z}\left(\varvec{\omega}\right) = {\mathbf{diag}}\left( {\varvec{K},\varvec{Z}_{1} , \ldots ,\varvec{Z}_{\varvec{j}} , \ldots ,\varvec{Z}_{{\varvec{n}_{\varvec{h}} }} } \right), $$

(C5)

where the $\varvec{Z}_{\varvec{j}} \varvec{ }(j = 1, 2, \ldots ,n_{h} )$ is defined as

$$ \varvec{Z}_{\varvec{j}} = \left[ {\begin{array}{*{20}c} { - \left( {\varvec{j\omega }} \right)^{2} \varvec{M} + \varvec{K}} & {\varvec{j\omega C}} \\ { - \varvec{j\omega C}} & { - \left( {\varvec{j\omega }} \right)^{2} \varvec{M} + \varvec{K}} \\ \end{array} } \right]. $$

(C6)

Equation (C6) is usually rewritten as a residual form,

$$ \varvec{R} = \varvec{Z}\left(\varvec{\omega}\right)\varvec{u} - \varvec{F}_{\varvec{e}} + \varvec{f}_{{\varvec{nl}}} , $$

(C7)

where $\varvec{R}$ is the residual. The residual equation is solved iteratively using a Newton–Raphson method for the steady response amplitude,

$$ \varvec{u}^{{\left( {\varvec{j} + 1} \right)}} = \varvec{u}^{{\left( \varvec{j} \right)}} - \left( {\left. {\frac{{\partial \varvec{R}}}{{\partial \varvec{u}}}} \right|_{{\varvec{u}^{{\left( \varvec{j} \right)}} }} } \right)^{ - 1} \varvec{R}\left( {\varvec{u}^{{\left( \varvec{j} \right)}} } \right), $$

(C8)

where $\frac{{\partial \varvec{R}}}{{\partial \varvec{u}}} = \varvec{Z}\left(\varvec{\omega}\right) + \frac{{\partial \varvec{f}_{{\varvec{nl}}} }}{{\partial \varvec{u}}}$ is the Jacobian matrix of the system.

Due to the dependent of friction force on relative displacement and velocity of contact interface and its hysteresis characteristics, it is hard to be obtained in frequency domain. Therefore, the AFT method is used to implement the mutual transformation of response signals between time and frequency domains.

After the initial response $\varvec{u}\left( \varvec{t} \right)$ in time domain is obtained, the friction force $\varvec{f}_{{\varvec{nl}}} \left( \varvec{t} \right)$ can be calculated using the proposed model. Then the friction force in time domain is transformed into frequency domain using a Fast Fourier Transform. Substituting the friction force, $\varvec{f}_{{\varvec{nl}}} \left(\varvec{\omega}\right)$, into Eq. (C4) and solving iteratively the algebraic equation to get a new steady solution, $\varvec{u}(\varvec{\omega})^{{\left( {\varvec{i} + 1} \right)}}$, the updated time domain solution, $\varvec{u}(\varvec{t})^{{\left( {\varvec{i} + 1} \right)}}$, can be obtained by an inverse Fast Fourier Transform. Subsequently, the friction force is updated according to new response. An iterative process is performed until the solution is convergent. That is, the residual $\varvec{R}$ is smaller than a given tolerance.