1 Introduction

At the end of 2019, a new viral disease was discovered in Wuhan, China. The scientists found that the cause of this infectious disease is the novel betacoronavirus, which leads to the severe acute respiratory syndrome. This virus, which is now known as 2019-nCoV, SARS-CoV-2, and COVID-19, affects the lungs and has symptoms such as cough, fever, tiredness, and difficult breathing. Unfortunately, the spread of the 2019-nCoV was too rapid in Hubei Province and became an epidemic at the end of January 2020. Consequently, the Chinese government imposed the quarantine restrictions to prevent the outbreak. International travels were also declared. However, it was not successful, and the disease was spread in the whole globe. At the time, a large number of countries such as the USA, Italy, Spain, and Germany are affected by this disease and the governments try to defeat coronavirus by enforcing social distancing.

The infectious pandemics have substantial effects on the health and also on finance. Therefore, the study of the dynamics of transmission of the disease is of great importance. By the help of mathematical tools, it is a possibility to predict many real-world time series in different fields such as economics, finance, and climate [1,2,3,4,5]. Mathematical models are an effective tool for understanding the dynamics of the outbreaks. These models are also useful in forecasting the spread of the disease and thus help the governments to be prepared and make necessary decisions [6]. The well-known and most used mathematical models for the spread of infections are the classical ordinary differential equations, such as SI, SIS, SIR, SEIR, SIRD, and SEIRD models. In these models, each variable represents the number of individuals in different groups. From the discovery of the 2019-nCoV, several models have been proposed to study its dynamics [7,8,9,10,11,12]. Zhong et al. [13] proposed a simple SIR model for predicting novel coronavirus, according to China’s first reported data. Yang and Wang [14] presented an extended SEIR model for COVID-19 with time-varying transmission rates by considering the environmental effects. Liang [15] described the growth propagation of three pandemic diseases, COVID-19, SARS, and MERS, by mathematical models and found that the growth rate of COVID-19 is much greater than SARS and MERS.

The fractional-order differential equations have been recently used for describing the behavior of the epidemics [16,17,18,19,20,21,22]. The fractional derivatives are dependent on the historical states, in addition to the current state, and thus have memory properties [17, 18]. Therefore, they are a better choice for the epidemic’s modeling. Furthermore, in the fractional model, the derivative order provides a degree of freedom in fitting data [18]. Due to these properties, the fractional differential equations have been used for various applications in different fields [23,24,25,26,27,28,29]. González–Parra et al. [18] presented a fractional-order SEIR model for explaining the outbreak of influenza A(H1N1). They showed that the fractional model agrees with the real data better than the classical model. Demirci et al. [16] proposed a fractional-order SEIR epidemic model with vertical transmission with considering that the death rate is dependent on the number of the total population. Area et al. [17] analyzed the data of the Ebola outbreak by both integer-order and fractional-order SEIR models. However, they reported that the classical model had better fitting results than the fractional one.

All of the studies in modeling the spread of COVID-19 have considered ordinary differential equations, while there are some claims that the fractional-order models have a better fitting to the real data. In [30], the authors have presented a SEIRD model for analyzing and predicting the COVID-19. In this paper, we analyze this model with fractional-order derivatives. We compute the error of fitting the model to the real data, which refers to Italy from February 24 to April 7. Therefore, the optimum parameters are found for different derivative orders. It is observed that the model with fractional order has less fitting error than the integer model. Then, the model is tested by using the data of April 8 to May 16 (unseen by the model during parameter estimation). The results show that the fractional model provides a better prediction than the integer model.

Fig. 1
figure 1

The estimation of the integer-order model. a The estimated (blue line) and the real (cyan circles) infected individuals. b The estimated (red line) and the real (magenta circles) deceased individuals. c Estimation of all populations (susceptible: green, exposed: orange, infected: blue, recovered: purple, deceased: red). The parameters are \( S(0)=3.6\times 10^6 \), \( E(0)=1.24\times 10^4 \), \( r_1=9.3 \times 10^{-8} \), \( a_1=0.17\). (Color figure online)

Full size image
Fig. 2
figure 2

The comparison between estimations with different derivative orders. a The estimated and the real infected individuals. b The estimated and the real deceased individuals. The parameters used for each derivative order are presented in Table 1

Full size image

2 SEIRD model

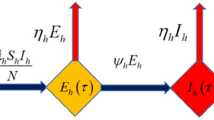
In our investigation, we use the SEIRD model proposed in [30], which contains five populations of susceptible individuals (S), the infected individuals who are not detected (asymptomatic) (E), the symptomatic (I), recovered (R), and deceased (D) individuals. The describing equations of this model are as follows:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} -S(r_1E+r_2I)\nonumber \\ \frac{\mathrm{d}E}{\mathrm{d}t}= & {} S(r_1E+r_2I)+(a_1+c_1)E\nonumber \\ \frac{\mathrm{d}I}{\mathrm{d}t}= & {} c_1E-(a_2+c_2)I\nonumber \\ \frac{\mathrm{d}R}{\mathrm{d}t}= & {} a_1E+a_2I\nonumber \\ \frac{\mathrm{d}D}{\mathrm{d}t}= & {} c_2I. \end{aligned}$$
(1)

This model assumes that the asymptomatic individuals can recover with the rate of \(a_1\) or become symptomatic with the rate of \(c_1\). Furthermore, the symptomatic individuals recover with the rate of \( a_2 \) or die with the rate of \( c_2 \). The rates of getting infected from the asymptomatic and symptomatic individuals are \( r_1 \) and \( r_2 \), respectively. According to [30], it is assumed that the detected infected individuals are in isolation, and thus, \( r_2=0 \) is considered. At the first stage of the epidemic, the total population is susceptible to the disease (\( S(0)=N \)). But by enforcing the social distancing, fewer people are susceptible, and therefore, the value taken for S(0) is reduced.

As in [30], we consider the sum of \( \alpha _1=a_1+c_1 \) and \( \alpha _2=a_2+c_2 \) to be the inverse of \( \tau _I \) and \( \tau _D \), respectively. The \( \tau _I=5 \) and \( \tau _D=11 \) are the mean time of incubation and the mean time from the initial symptoms to death. The mortality rate is also set at 0.02 and is calculated by \( m=\frac{c_1}{\alpha _1} \frac{c_2}{\alpha _2} \). Therefore, by setting the parameters \( a_1 \), \( r_1 \), S(0) , and E(0) from the best fit and by using these equations, all of the parameters are obtained as follows: \(c_1=\alpha _1-a_1\)\(c_2=m\frac{\alpha _1\alpha _2}{c_1}\)

\(a_2=\alpha _2-c-2\).

3 Fractional SEIRD model

There are several definitions for the fractional derivatives. Among them, the Caputo-type fractional derivative is more popular and used for real applications. The Caputo-type fractional derivative is defined by:

$$\begin{aligned} D^q f(t)= & {} \frac{1}{\varDelta (n-q)}\int _{0}^{t}(t-\tau )^{n-q-1}f^{(n)}(\tau )\mathrm{d}\tau =\nonumber \\&j^{(n-q)}\left( \frac{\mathrm{d}^n}{\mathrm{d}t^n}f(t)\right) , \end{aligned}$$
(2)

where \( n=[q] \) is the first integer greater than q, \(\varDelta \) is the gamma function, and \( j^\alpha \) is the \(\alpha \)-order Riemann–Liouville integral operator expressed by:

$$\begin{aligned} j^\alpha f(t)=\frac{1}{\varDelta (\alpha )}\int _{0}^{t}(t-\tau )^{\alpha -1}f(\tau )d\tau . \end{aligned}$$
(3)

Now, we write the SEIRD model (Eq. 1) with fractional derivatives as:

$$\begin{aligned} D^\alpha S= & {} -S(r_1E+r_2I)\nonumber \\ D^\alpha E= & {} S(r_1E+r_2I)+(a_1+c_1)E\nonumber \\ D^\alpha I= & {} c_1E-(a_2+c_2)I\nonumber \\ D^\alpha R= & {} a_1E+a_2I\nonumber \\ D^\alpha D= & {} c_2I \end{aligned}$$
(4)

where all the parameters are defined the same as the classical model, and q is the derivative order. As in the classical model, the values of the \( a_1 \), \( r_1 \), E(0) , and S(0) are estimated from the best fit of the model and the real data. Then, the values of \( c_1 \), \( c_2 \), and \( \alpha _2 \) are computed from the equations. For the numerical solutions of the fractional model (Eq. 4), we use the Adams–Bashforth–Moulton predictor–corrector scheme [31].

Theorem 1

There is a unique nonnegative solution for the fractional differential equations given by Eq. 4.

Proof

The existence and uniqueness of the solution of Eq. 4 can be attained by applying ([32], Theorem 3.1, and Remark 3.2). According to [16], we must show that the domain \(R^4_+\) is positively invariant: \( D^\alpha S |_{S=0}=0\)

\( D^\alpha E |_{E=0}=0\)

\( D^\alpha I |_{I=0}=c_1E\)

\( D^\alpha R |_{R=0}=a_1E+a_2I\)

\( D^\alpha D |_{D=0}=c_2I\).

Thus, all of the above equations are \(\ge 0\). Therefore, by using ([16], Lemma 3.1, and Remark 3.2) Theorem 1 is proved and the solution remains in \(R^4_+\).

Table 1 The values of the optimum parameters for each derivative order
Full size table

4 Results

To estimate the parameters of the model, we use Italy’s data from February 24 to April 7, reported by WHO. We consider the number of the infected (I) and deceased (D) individuals and compute the root-mean-square error (RMSE) to find the optimal parameters:

$$\begin{aligned} \text {RMSE}=\sqrt{\frac{\sum _{t=1}^{T}(I_r-I_m)^2+(D_r-D_m)^2}{T}}, \end{aligned}$$
(5)

where r and m denote the real data and the model, respectively, and T is the time of available data. The initial values are adopted according to the data in February 24 as \( I(0)=221 \), \( R(0)=1 \), and \( D(0)=7 \). Firstly, the integer-order model is studied, and the best parameters are obtained.

Fig. 3
figure 3

The normalized root-mean-square error of the model estimation for different derivative orders. The minimum error of estimation is obtained for \( q=0.725 \)

Full size image

Figure 1 shows the best estimation of the classical model by fixing \( S(0)=3.6 \times 10^6 \), \( E(0)=1.24\times 10^4 \), \( r_1=9.3\times 10^{-8} \), and \( a_1=0.17 \). The value of the normalized root-mean-square error is 0.0202. In Fig. 1a, the estimated (blue line) and real values (cyan circles) of the infected individuals (I) are shown, and the estimated (red line) and real values (magenta circles) of the deaths are illustrated in Fig. 1b. Figure 1c depicts all of the models variables in the logarithmic scale, wherein the susceptible, exposed, and recovered individuals are shown in green, orange, and purple, respectively. This estimation predicted that the number of infected individuals would be maximum on April 9.

Fig. 4
figure 4

The estimation of the fractional-order model with \( q=0.725 \). a The estimated (blue line) and the real (cyan circles) infected individuals. b The estimated (red line) and the real (magenta circles) deceased individuals. c Estimation of all populations (susceptible: green, exposed: orange, infected: blue, recovered: purple, deceased: red). The parameters are \( S(0)=5.32 \times 10^6 \), \( E(0)=1.16 \times 10^4 \), \( r_1=9.4 \times 10^{-8} \), \( a_1=0.185\). (Color figure online)

Full size image

Next, the fractional-order model is investigated by varying the derivative order. The results of the estimation of the infected and dead populations for different orders are shown in Fig. 2. As the figure shows, the slope and the peak of the estimation are changed by varying the derivative order. To find the optimum order for the fractional model, we have calculated the RMSE for each order and found the best fit. Figure 3 shows the value of the normalized RMSE concerning the derivative order. The values of the parameters at which these errors have been obtained are presented in Table 1. Figure 3 represents that by decreasing the derivative order, the error of estimation is decreased until \( q=0.725 \). Then, by more decreasing the order, the error increases. Therefore, according to this diagram, the best fit is obtained by setting \( q=0.725 \), with \( RMSE=0.0082 \). Figure 4 shows the results for \( q=0.725 \), at which the parameters are fixed at \( S(0)=5.32 \times 10^6 \), \( E(0)=1.16 \times 10^4 \), \( r_1=9.4 \times 10^{-8} \), and \( a_1=0.185 \). This estimation predicted that the peak of the infected population would occur on 15 April.

Fig. 5
figure 5

The prediction of the integer- and fractional-order (\( q=0.725 \)) models. The data used for estimating the parameters are shown by blue circles, and the test data are shown by blue stars. The estimation of the integer- and fractional-order models is represented by red and green, respectively. The values of the parameters are given in Table 1. (Color figure online)

Full size image

In order to compare the integer and fractional models’ prediction ability, another set of real data is used. As mentioned before, for estimating the parameters of the models, the data from February 24 to April 7 have been used. To check the prediction of the models, we use the data from April 8 to May 16. In Fig. 5, the blue circles show the samples used for evaluating the models, and the blue stars show the test data set. The estimation of the integer and fractional models is represented by red and green, respectively. It is observed that the integer model is only valid for the first data set and does not perform well in forecasting the unseen data. But the fractional model not only has less error in modeling main data, but is also much closer to real test data (better performance in forecasting).

5 Discussion and conclusion

In December 2019, a novel coronavirus was discovered in China and very rapidly affected other countries. In this paper, in order to understand and predict the spread of this epidemic, we analyzed the outbreak of the novel coronavirus in Italy, acquired from World Health Organization (WHO). Recently, a SEIRD model that considers the susceptible, exposed, infected, recovered, and deceased populations has been proposed for this disease [30]. Here, we considered the SEIRD model with fractional derivatives to model the outbreak. The fractional-order equations are usually more efficient in modeling since the choice of the derivative order provides one more degree of freedom. For the fractional model, the Caputo operator was considered, and the Adams–Bashforth–Moulton predictor–corrector scheme was used for solving the equations. Firstly, the data from February 24 to April 7 were used for finding the model’s parameters with the best fit. The parameters were obtained by computing the minimum root-mean-square error of fitting the model to the real data. The results showed that the factional-order model provides a better fit to the real data with less error than the integer-order model. The best fit was attained for the derivative order \( q=0.725 \). Then, the data from April 8 to May 16 were used to check the prediction of the integer and fractional models. It was observed that the fractional model has a closer estimation of the reality. The fractional model predicts the peak of the outbreak to be on April 15. While in the estimation of the integer-order model, the peak occurs on April 9. According to the obtained results, it is suggested to use fractional-order models in the prediction of many real-world time series in different fields such as economics, finance, and climate.