Skip to main content
SpringerLink
Log in

Complex dynamics of a non-volatile memcapacitor-aided hyperchaotic oscillator

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

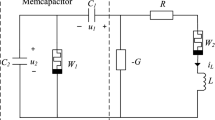
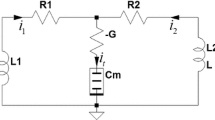
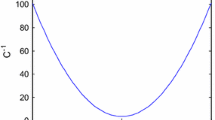
To explore memcapacitors and their characteristics in chaotic oscillators, this paper proposes a logarithmic charge-controlled memcapacitor model. Using power-off plot analysis, we show that the memcapacitor possesses continuous non-volatile characteristic. Also, its dynamic route map shows the memcapacitor can rapidly switch from one memcapacitance to another by applying a single voltage pulse. Based on the memcapacitor model, we design a chaotic oscillator, which can exhibit some complex dynamic characteristics, such as chaos, hyperchaos and various coexisting attractors. The multistable coexisting oscillation of the system is further analyzed by using phase portraits, basins of attraction and double-bifurcation diagrams. Symmetric coexistence attractors with infinite homogeneity and heterogeneity are also found, which can evolve into hyperchaos under certain initial conditions. Finally, the chaotic oscillator is verified by numerical simulations and digital signal processor experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Yuan, F., Deng, Y., Li, Y.X., Wang, G.Y.: The amplitude, frequency and parameter space boosting in a memristor–meminductor-based circuit. Nonlinear Dyn. 56, 1–17 (2019)

    Google Scholar 

  2. Liu, Z., Wu, F., Alzahrani, F., Ma, J.: Control of multi-scroll attractors in a memristor-coupled resonator via time-delayed feedback. Mod. Phys. Lett. B 32, 1850399 (2018)

    Article  MathSciNet  Google Scholar 

  3. Wen, S.P., Wei, H.Q., Yang, Y., Guo, Z.Y., Zeng, Z.G.: Memristive LSTM network for sentiment analysis. IEEE Trans. Syst. Man Cyber. Syst. 49, 1–11 (2019)

    Article  Google Scholar 

  4. Yu, D.S., Zheng, C.Y., Iu, H.H.C., Fernando, T., Chua, L.O.: A new circuit for emulating memristor using inductive coupling. IEEE Access 5, 1284–1295 (2017)

    Article  Google Scholar 

  5. Ying, J.J., Wang, G.Y., Dong, Y.J., Yu, S.M.: Switching characteristics of a locally-active memristor with binary memories. Int. J. Bifurc. Chaos 29, 1930030 (2019)

    Article  MathSciNet  Google Scholar 

  6. Chua, L.O.: Five non-volatile memristor enigmas solved. Appl. Phys. A 124, 563–606 (2018)

    Article  Google Scholar 

  7. Yuan, F., Wang, G.Y., Shen, Y.R.: Coexisting attractors in a memcapacitor-based chaotic oscillator. Nonlinear Dyn. 86, 1–14 (2016)

    Article  MathSciNet  Google Scholar 

  8. Zhou, Z., Zhu, W., Zhu, H., Yu, D.S.: Two-stable-oscillator circuit based on coupling memcapacitor simulator. J. Power Supply 16, 171–177 (2018)

    Google Scholar 

  9. Karthikeyan, R., Sajad, J., Anitha, K., Ashokkumar, S., Biniyam, A.: Hyperchaotic memcapacitor oscillator with infinite equilibria and coexisting attractors. Circ. Syst. Signal Process. 7, 1–23 (2018)

    Article  MathSciNet  Google Scholar 

  10. Wang, G.Y., Yuan, F., Chen, G.R., Zhang, Y.: Coexisting multiple attractors and riddled basins of a memristive system. Chaos 28, 013125 (2018)

    Article  MathSciNet  Google Scholar 

  11. Bao, B.C., Li, Q.D., Wang, N., Xu, Q.: Multistability in Chua’s circuit with two stable node-foci. Chaos 26, 043111 (2016)

    Article  MathSciNet  Google Scholar 

  12. Yuan, F., Li, Y.X.: A chaotic circuit constructed by a memristor, a memcapacitor and a meminductor. Chaos 29, 101101 (2019)

    Article  MathSciNet  Google Scholar 

  13. Chen, M., Sun, M.X., Bao, B.C., Wu, H.G., Xu, Q., Wang, J.: Controlling extreme multistability of memristor emulator-based dynamical circuit in flux-charge domain. Nonlinear Dyn. 91, 1395–1412 (2018)

    Article  Google Scholar 

  14. Suhas, K., John, P.S., Williams, R.S.: Chaotic dynamics in nanoscale NbO\(_2\) Mott memristors for analogue computing. Nature 548, 7667 (2017)

    Google Scholar 

  15. Zhou, W., Wang, G.Y., Shen, Y., Yuan, F., Yu, S.M.: Hidden coexisting attractors in a chaotic system without equilibrium point. Int. J. Bifurc. Chaos 28, 1830033 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work was supported by the National Natural Science Foundation of China under Grants 61771176 and 61801154.

Author information

Authors and Affiliations

  1. Institute of Modern Circuit and Intelligent Information, Hangzhou Dianzi University, Hangzhou, 310018, China

    Wei Zhou, Guangyi Wang, Yiran Shen & Yan Liang

  2. School of Electrical, Electronic, and Computer Engineering, The University of Western Australia, Perth, WA, 6009, Australia

    H. H. C. Iu

Authors
  1. Wei Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guangyi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. H. C. Iu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yiran Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yan Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guangyi Wang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, W., Wang, G., Iu, H.H.C. et al. Complex dynamics of a non-volatile memcapacitor-aided hyperchaotic oscillator. Nonlinear Dyn 100, 3937–3957 (2020). https://doi.org/10.1007/s11071-020-05722-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05722-3

Keywords

Search

Navigation