Abstract
Nowadays, social interactions among customers play an increasingly important role in product demand. However, the existing literature mostly focusses on the social influence of other customers’ stated preference while disregarding the social influence of revealed preference. To bridge the gap, this paper incorporates the latter, referred to as herd behavior of customers, into a dynamic demand–supply system of fast moving consumer goods, whose sales to some extent depend on social interaction. Equilibrium points and their local stability are analyzed first. Then, we solve the optimal supply strategy and analyze the evolution characteristics of this demand–supply dynamics. Results indicate that there may be more than one equilibrium point in this system. Provider has two optimal supply policies if initial point is the indifference point, which separates state space if two steady states exist. In addition, the demand–supply evolution is periodic as the provider alternates between cultivating and exploiting the herd effect.











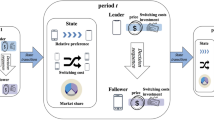
(figures come from http://tech.ifeng.com/a/20181126/45235137_0.shtml)
Similar content being viewed by others
References
El Ouardighi, F., Feichtinger, G., Grass, D., Hartl, R., Kort, P.M.: Autonomous and advertising-dependent ’word of mouth’ under costly dynamic pricing. Eur. J. Oper. Res. 251(3), 860–872 (2016)
Crapis, D., Ifrach, B., Maglaras, C., Scarsini, M.: Monopoly pricing in the presence of social learning. Manag. Sci. 63(11), 3586–3608 (2016)
Yuan, X., Hwarng, H.B.: Stability and chaos in demand-based pricing under social interactions. Eur. J. Oper. Res. 253(2), 472–488 (2016)
Viglia, G., Furlan, R., Ladron-de Guevara, A.: Please, talk about it! when hotel popularity boosts preferences. Int. J. Hosp. Manag. 42, 155–164 (2014)
Engström, P., Forsell, E.: Demand effects of consumers’ stated and revealed preferences. J. Econ. Behav. Organ. 150, 43–61 (2018)
Chen, Y.-F.: Herd behavior in purchasing books online. Comput. Hum. Behav. 24(5), 1977–1992 (2008)
Banerjee, A.V.: A simple model of herd behavior. Q. J. Econ. 107(3), 797–817 (1992)
Bikhchandani, S., Hirshleifer, D., Welch, I.: A theory of fads, fashion, custom, and cultural change as informational cascades. J. Polit. Econ. 100(5), 992–1026 (1992)
Gutierrez, G.J., He, X.: Life-cycle channel coordination issues in launching an innovative durable product. Prod. Oper. Manag. 20(2), 268–279 (2011)
Van Ackere, A., Haxholdt, C., Larsen, E.R.: Dynamic capacity adjustments with reactive customers. Omega 41(4), 689–705 (2013)
Jiang, B., Yang, B.: Quality and pricing decisions in a market with consumer information sharing. Manag. Sci. (2018). https://doi.org/10.1287/mnsc.2017.2930
Yao, J., Ma, C., He, W.P.: Investor herding behaviour of chinese stock market. Int. Rev. Econ. Finance 29, 12–29 (2014)
Yang, X., Gao, M., Wu, Y., Jin, X.: Performance evaluation and herd behavior in a laboratory financial market. J. Behav. Exp. Econ. 75, 45–54 (2018)
Zhang, J., Liu, P.: Rational herding in microloan markets. Manag. Sci. 58(5), 892–912 (2012)
Veeraraghavan, S.K., Debo, L.G.: Herding in queues with waiting costs: rationality and regret. Manuf. Serv. Oper. Manag. 13(3), 329–346 (2011)
Liu, Y.: Word of mouth for movies: its dynamics and impact on box office revenue. J. Marketing 70(3), 74–89 (2006)
Duan, W., Gu, B., Whinston, A.B.: The dynamics of online word-of-mouth and product sales-an empirical investigation of the movie industry. J. Retail. 84(2), 233–242 (2008)
Ma, J., Wang, H.: Complexity analysis of dynamic noncooperative game models for closed-loop supply chain with product recovery. Appl. Math. Model. 38(12), 5562–5572 (2014)
Ma, J., Xie, L.: The comparison and complex analysis on dual-channel supply chain under different channel power structures and uncertain demand. Nonlinear Dyn. 83(3), 1379–1393 (2016)
Ma, J., Sun, L.: Complexity analysis about nonlinear mixed oligopolies game based on production cooperation. IEEE Trans. Control Syst. Technol. 26(4), 1532–1539 (2018)
Ma, J., Ren, H.: Influence of government regulation on the stability of dual-channel recycling model based on customer expectation. Nonlinear Dyn. 93(3), 1775–1790 (2018)
Chen, Y.C., Fang, S.-C., Wen, U.-P.: Pricing policies for substitutable products in a supply chain with internet and traditional channels. Eur. J. Oper. Res. 224(3), 542–551 (2013)
Zhang, S., Zhang, J.: Contract preference with stochastic cost learning in a two-period supply chain under asymmetric information. Int. J. Prod. Econ. 196, 226–247 (2018)
Popescu, I., Wu, Y.: Dynamic pricing strategies with reference effects. Oper. Res. 55(3), 413–429 (2007)
Wu, F., Ma, J.: The equilibrium, complexity analysis and control in epiphytic supply chain with product horizontal diversification. Nonlinear Dyn. 93(4), 2145–2158 (2018)
Ma, J., Lou, W., Tian, Y.: Bullwhip effect and complexity analysis in a multi-channel supply chain considering price game with discount sensitivity. Int. J. Prod. Res. 57(17), 5432–5452 (2019)
Guo, Z.: Complexity and implications on channel conflict under the uncertain impacts of online customer reviews. Nonlinear Dyn. 96(3), 1971–1987 (2019)
Medio, A., Lines, M.: Nonlinear Dynamics: A Primer. Cambridge University Press, Cambridge (2001)
Guo, Z., Ma, J.: Dynamics and implications on a cooperative advertising model in the supply chain. Commun. Nonlinear Sci. Numer. Simul. 64, 198–212 (2018)
Ruan, S., Wang, W.: Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equ. 188(1), 135–163 (2003)
Kiseleva, T.: Heterogeneous beliefs and climate catastrophes. Environ. Resour. Econ. 65(3), 599–622 (2016)
Moghayer, S.M., et al.: Bifurcations of indifference points in discrete time optimal control problems. Thela thesis (2012)
Lenhart, S., Workman, J.T.: Optimal Control Applied to Biological Models. CRC Press, Boca Raton (2007)
González-Parra, P.A., Lee, S., Velazquez, L., Castillo-Chavez, C.: A note on the use of optimal control on a discrete time model of influenza dynamics. Math. Biosci. Eng. 8(8), 183–197 (2011)
Grass, D., Caulkins, J., Feichtinger, G., Tragler, G., Behrens, D.: Optimal Control of Nonlinear Processes: With Applications in Drugs, Corruption, and Terror. Springer, Berlin (2008)
Acknowledgements
The authors thank the reviewers for valuable comments and pertinent suggestions. This research was supported by the National Natural Science Foundation of China (No.71571131).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Proof of Proposition 2
As \(\mu ' = 1 - \frac{{\Omega '(\Lambda )\phi (p) - \Omega (\Lambda )\phi '(p)h'(\Lambda )}}{{{\phi ^2}(p)}}\), for any equilibrium point \(({\Lambda ^*},{p^*};\mu )\) in a decreasing interval of \(f( \Lambda )\), \({\mathrm{P}}({\mathrm{1}}){\mathrm{= 1 + }}v(1 - \phi + \Omega ') - (1 - \phi + v + \Omega ' + (\mu - \Lambda )(1 - v)h'\phi ')=({\mathrm{1}} - v)[\phi ({p^*}) - \Omega '({\Lambda ^*}) - (\mu - {\Lambda ^*})h'({\Lambda ^*})\phi '({p^*})]=({\mathrm{1}} - v)\phi ({p^*})\mu ' < 0\) holds, so this equilibrium point is always unstable. For the equilibrium point in an increasing interval, \({\mathrm{P(1)}}>0\) and \({\mathrm{P}}( - {\mathrm{1}}){\mathrm{= 1 + }}v(1 - \phi + \Omega ') + (1 - \phi + \Omega ' + v + (\mu - \Lambda )(1 - v)h'\phi ')=(1 + v)(2 - \phi + \Omega ') + (\mu - \Lambda )(1 - v)h'\phi ' \ge (1 + v)(2 - \mu '\phi ({p^*})) > 0\) when \(\mu '({\Lambda ^{\mathrm{*}}})\phi ({p^{\mathrm{*}}}) < 2\). In addition, \(\det (J)<1\) always holds if \(\Omega '({\Lambda ^{\mathrm{*}}}) < \phi ({p^*})\), so Jury stability condition is satisfied and the equilibrium point is asymptotically stable. However, if \(\Omega '({\Lambda ^{\mathrm{*}}}) >\phi ({p^*})\), Jury stability condition will be violated due to \(\det (J)>1\) with the increase in v.
This is to say, when v crosses \({v^{\mathrm{0}}} = \frac{1}{{1 - \phi ({p^*}) + \Omega '({\Lambda ^*})}}\) from the left side, a pair of complex-conjugate eigenvalues crosses the unit circle [28]. As a consequence, the equilibrium point becomes unstable. \(\square \)
Proof of Proposition 3
For a given \({\chi _t} \), \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}} = w{\Lambda _t} - 2\alpha {q_t} + {\chi _t}\frac{{{{\mathrm{e}}^{w{\Lambda _t} + \alpha {q_t}}}\alpha ({\Lambda _t} - \mu )}}{{{{({{\mathrm{e}}^{w{\Lambda _t}}} + {{\mathrm{e}}^{\alpha {q_t}}})}^2}}} \). As \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}} >0\) when \({q_t}=0\) and \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}}<0\) when \({q_t} \rightarrow \infty \), so \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}} =0\) must have solution(s) in \({q_t} \in (0,\infty )\). The second-order derivative satisfies \(\frac{{{\partial ^2}{\mathcal {H}}}}{{{\partial }{q_t}^2}} = \frac{{{{\mathrm{e}}^{w{\Lambda _t} + \alpha {q_t}}}({{\mathrm{e}}^{w{\Lambda _t}}} - {{\mathrm{e}}^{\alpha {q_t}}})}}{{{{({{\mathrm{e}}^{w{\Lambda _t}}} + {{\mathrm{e}}^{\alpha {q_t}}})}^3}}} \)\({\alpha ^2}({\Lambda _t} - \mu ){\chi _t} - 2\alpha \). Any solution of \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}} =0\) also satisfies \(\frac{{{\partial ^2}\mathcal{H}}}{{\partial {q_t}^2}} = \alpha \frac{{{{\mathrm{e}}^{w{\Lambda _t}}} - {{\mathrm{e}}^{\alpha {q_t}}}}}{{{{\mathrm{e}}^{w{\Lambda _t}}} + {{\mathrm{e}}^{\alpha {q_t}}}}}( 2\alpha {q_t}-w{\Lambda _t}) - 2\alpha < 0\). Therefore, this solution must be a local maximum. If there are two local maximums, there must be a local minimum between them. This contradicts with \(\frac{{{\partial ^2}\mathcal{H}}}{{\partial {q_t}^2}} < 0\). So \(\frac{{\partial \mathcal{L}}}{{\partial {q_t}}} =0\) has a unique solution. Assume the unique solution of \(\frac{{\partial {\mathcal {H}}}}{{\partial {q_t}}} =0\) is \({{\hat{q}}_t}\). Then, if \({{\hat{q}}_t}\) satisfies \({{\hat{q}}_t}<w\Lambda _t\), \({{\hat{q}}_t}\) also is the unique solution of \(\frac{{\partial \mathcal{L}}}{{\partial {q_t}}} =0\) with \({\eta _t} =0\). If \({{\hat{q}}_t}>w\Lambda _t\), \(\frac{{\partial \mathcal{L}}}{{\partial {q_t}}} =0\) has a unique solution \({q_t} = \frac{{w{\Lambda _t}}}{\alpha }\) with \({\eta _t} = {\chi _t}\frac{{({\Lambda _t} - \mu )}}{4} - \frac{w}{\alpha }{\Lambda _t}\). What is more, Legendre–Clebsch condition is satisfied for the interior solution. \(\square \)
Appendix B
Step 1 Initialize decision variable \({q_t}\) and the slack variable \({\eta _t} =0\), \(t=1,2,\ldots ,T\),
Step 2 Solve state variable \({\Lambda _t}\) (\({\Lambda _t}\) and \({r_t}\)) in Eq. 8 (Eq. 7) forward in time,
Step 3 Solve adjoint variable \({\chi _t}\) (\({\chi _t}\) and \({\kappa _t}\)) via Eq. 10 (Eq. 12 and Eq. 13) backward in time, subject to transversality condition \({\chi _T}=0\) (\({\chi _T}=0\) and \({\kappa _T}=0\)),
Step 4 Solve decision variable \({q_t}\) via Proposition 3 (Proposition 4),
Step 5 Check convergence. If \(\left\| \mathbf{q - \mathbf q _{old}} \right\| > {10^{ - 4}}\), go to Step 2. Otherwise, stop and output \({q_t}\) and the corresponding profit.
Rights and permissions
About this article
Cite this article
Ma, J., Guo, Z. & Hong, Y. Demand–supply dynamics in FMCG business: exploration of customers’ herd behavior. Nonlinear Dyn 98, 1669–1681 (2019). https://doi.org/10.1007/s11071-019-05278-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-05278-x