Skip to main content
SpringerLink
Log in

Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

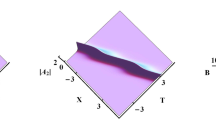
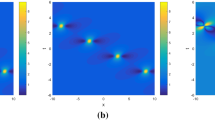
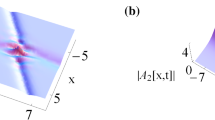
Investigated in this paper is a non-autonomous generalized AB system, which is used to describe certain baroclinic instability processes in the geophysical flows. We discover that the two short waves and mean flow can evolve in the forms of the multi-rogue waves on the condition that the nonlinearity effect \(\sigma \) is positive. Via the Darboux and generalized Darboux transformations, we obtain the first- and second-order rogue waves as well as the algorithm to derive the Nth-order rogue waves. It is revealed that the perturbation function \(\delta (t)\) has no effect on the two short waves while affects the mean flow by changing its evolution background. When \(\sigma \) is negative, those rogue waves turn to be singular. In addition, we find that the two short waves and mean flow can also appear as the solitary waves, and they perform as the “bright” solitons under \(\sigma >0\) while perform as the “dark” solitons under \(\sigma <0\). With the Hirota method, introducing the auxiliary function \(\alpha (t)\), we derive the first- and second-order bright and dark solitary waves. Both solitary wave velocities are related to \(\delta (t)\) and \(\alpha (t)\). Besides, \(\delta (t)\) and \(\alpha (t)\) have no effect on the amplitudes of the two short waves but bring about controllable backgrounds and deformations of the solitary waves for the mean flow.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Acheson, D.J.: Elementary Fluid Dynamics. Oxford University Press, London (1990)

    MATH  Google Scholar 

  2. Zhen, H.L., Tian, B., Sun, Y., Chai, J., Wen, X.Y.: Solitons and chaos of the Klein–Gordon–Zakharov system in a high-frequency plasma. Phys. Plasmas 22, 102304 (2015)

    Article  Google Scholar 

  3. Hasegawa, A., Tappert, F.: Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 23(3), 142–144 (1973)

    Article  Google Scholar 

  4. Wazwaz, A.M., El-Tantawy, S.A.: New \((3+1)\)-dimensional equations of Burgers type and Sharma–Tasso–Olver type: multiple-soliton solutions. Nonlinear Dyn. 87(4), 2457–2461 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  5. Pelinovsky, E., Kharif, C.: Extreme Ocean Waves. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  6. Osborne, A.R.: Nonlinear Ocean Waves and The Inverse Scattering Transform. Elsevier, New York (2010)

    MATH  Google Scholar 

  7. Korteweg, D.J., De Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39(5), 422–443 (1895)

    Article  MathSciNet  MATH  Google Scholar 

  8. Wang, L., Zhu, Y.J., Qi, F.H., Li, M., Guo, R.: Modulational instability, higher-order localized wave structures, and nonlinear wave interactions for a nonautonomous Lenells–Fokas equation in inhomogeneous fibers. Chaos 25(6), 063111 (2015)

    Article  MathSciNet  Google Scholar 

  9. Liu, L., Tian, B., Yuan, Y.Q., Du, Z.: Dark-bright solitons and semirational rogue waves for the coupled Sasa–Satsuma equations. Phys. Rev. E 97(5), 052217 (2018)

    Article  MathSciNet  Google Scholar 

  10. Wu, C.F., Grimshaw, R.H.J., Chow, K.W., Chan, H.N.: A coupled “AB” system: rogue waves and modulation instabilities. Chaos 25(10), 103113 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  11. Guo, R., Hao, H.Q., Zhang, L.L.: Dynamic behaviors of the breather solutions for the AB system in fluid mechanics. Nonlinear Dyn. 74(3), 701–709 (2013)

    Article  MathSciNet  Google Scholar 

  12. Wang, L., Wang, Z.Q., Sun, W.R., Shi, Y.Y., Li, M., Xu, M.: Dynamics of peregrine combs and peregrine walls in an inhomogeneous Hirota and Maxwell-Bloch system. Commun. Nonlinear Sci. Numer. Simul. 47, 190–199 (2017)

    Article  MathSciNet  Google Scholar 

  13. Hasimoto, H., Ono, H.: Nonlinear modulation of gravity waves. J. Phys. Soc. Jpn. 33(3), 805–811 (1972)

    Article  Google Scholar 

  14. Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34(1), 62–69 (1972)

    MathSciNet  Google Scholar 

  15. Zhou, Q., Zhu, Q.P., Liu, Y.X., Yu, H., Yao, P., Biswas, A.: Thirring optical solitons in birefringent fibers with spatio-temporal dispersion and Kerr law nonlinearity. Laser Phys. 25(1), 015402 (2015)

    Article  Google Scholar 

  16. Zhou, Q., Zhu, Q.P., Liu, Y.X., Yu, H., Wei, C., Yao, P., Bhrawy, A.H., Biswas, A.: Bright, dark and singular optical solitons in a cascaded system. Laser Phys. 25(2), 025402 (2015)

    Article  Google Scholar 

  17. Hirota, R.: The Direct Method in Soliton Theory. Springer, Berlin (1980)

    Google Scholar 

  18. Ohta, Y., Yang, J.K.: General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc. R. Soc. A 468(2142), 1716–1740 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Guo, B.L., Ling, L.M., Liu, Q.P.: Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E 85(2), 026607 (2012)

    Article  Google Scholar 

  20. Wang, L., Zhang, J.H., Liu, C., Li, M., Qi, F.H.: Breather transition dynamics, Peregrine combs and walls, and modulation instability in a variable-coefficient nonlinear Schrödinger equation with higher-order effects. Phys. Rev. E 93(6), 062217 (2016)

    Article  MathSciNet  Google Scholar 

  21. Wazwaz, A.M.: Two-mode fifth-order KdV equations: necessary conditions for multiple-soliton solutions to exist. Nonlinear Dyn. 87(3), 1685–1691 (2017)

    Article  MathSciNet  Google Scholar 

  22. Sun, W.R., Wang, L.: Matter rogue waves for the three-component Gross–Pitaevskii equations in the spinor Bose–Einstein condensates. Proc. R. Soc. A 474(2209), 20170276 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  23. Sun, W.R., Liu, D.Y., Xie, X.Y.: Vector semirational rogue waves and modulation instability for the coupled higher-order nonlinear Schrödinger equations in the birefringent optical fibers. Chaos 27(4), 043114 (2017)

    Article  MATH  Google Scholar 

  24. Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6(10), 790–795 (2010)

    Article  Google Scholar 

  25. Bailung, H., Sharma, S.K., Nakamura, Y.: Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 107(25), 255005 (2011)

    Article  Google Scholar 

  26. Porsezian, K., Daniel, M., Lakshmanan, M.: On the integrability aspects of the one-dimensional classical continuum isotropic biquadratic Heisenberg spin chain. J. Math. Phys. 33(5), 1807–1816 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dai, C.Q., Wang, Y., Liu, J.: Spatiotemporal hermite–gaussian solitons of a \((3+1)\)-dimensional partially nonlocal nonlinear Schrödinger equation. Nonlinear Dyn. 84(3), 1157–1161 (2016)

    Article  MATH  Google Scholar 

  28. Pedlosky, J.: Finite-amplitude baroclinic waves. J. Atmos. Sci. 27, 15–30 (1970)

    Article  Google Scholar 

  29. Gibbon, J.D., James, I.N., Moroz, I.M.: An example of soliton behaviour in a rotating baroclinic fluid. Proc. R. Soc. Lond. A. 367, 219–237 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  30. Moroz, I.M., Brindley, J.: Evolution of baroclinic wave packets in a flow with continuous shear and stratification. Proc. R. Soc. Lond. A 377(1771), 379–404 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  31. Tan, B., Boyd, J.P.: Envelope solitary waves and periodic waves in the AB equations. Stud. Appl. Math 109(2), 67–87 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  32. Gibbon, J.D., James, I.N., Moroz, I.M.: An example of soliton behavior in a rotating baroclinic fluid. Proc. R. Soc. Lond. A 367(1729), 219–237 (1979)

    Article  MATH  Google Scholar 

  33. Yu, G.F., Xu, Z.W., Hu, J., Zhao, H.Q.: Bright and dark soliton solutions to the AB system and its multi-component generalization. Commun. Nonlinear Sci. Numer. Simul. 47, 178–189 (2017)

    Article  MathSciNet  Google Scholar 

  34. Dodd, R.K., Eilkck, J.C., Gibbon, J.D., Moms, H.C.: Solitons and Nonlinear Wave Equations. Academic, New York (1982)

    Google Scholar 

  35. Jiang, X.H., Gao, Y.T., Gao, X.Y.: Investigation on the behaviors of the soliton solutions for a variable-coefficient generalized AB system in the geophysical flows. Mod. Phys. Lett. B 31(28), 1750254 (2017)

    Article  MathSciNet  Google Scholar 

  36. Ablowitz, M.J., Kaup, D.J., Newell, A.C., Segur, H.: Nonlinear-evolution equations of physical significance. Phys. Rev. Lett. 31(2), 125–127 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  37. Zakharov, V.E., Shabat, A.B.: A scheme for integrating the nonlinear equations of mathematical physics by the method of the inverse scattering problem. I. Func. Anal. Appl. 8(3), 226–235 (1974)

    Article  MATH  Google Scholar 

  38. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 19(19), 1095–1097 (1967)

    Article  MATH  Google Scholar 

  39. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Korteweg–de Vries equation and generalizations. VI. methods for exact solution. Commun. Pure. Appl. Math. 27(1), 97–133 (1974)

    Article  MATH  Google Scholar 

  40. Liu, X.Y., Triki, H., Zhou, Q., Liu, W.J., Biswas, A.: Analytic study on interactions between periodic solitons with controllable parameters. Nonlinear Dyn. 94, 703–709 (2018)

    Article  Google Scholar 

  41. Gu, C.H., Hu, H.S., Zhou, Z.X.: Darboux Transformation in Soliton Theory and Its Geometric Applications. Shanghai Scientific and Technical Publishers, Shanghai (2005)

    Google Scholar 

  42. Caieniello, E.R.: Combinatorics and Renormalization in Quantum Field Theory. Benjamin, New York (1973)

    Google Scholar 

  43. Miura, M.R.: Bäcklund Transformation. Springer, Berlin (1978)

    Google Scholar 

  44. Dai, C.Q., Wang, Y.Y.: Controllable combined Peregrine soliton and Kuznetsov–Ma soliton in PT-symmetric nonlinear couplers with gain and loss. Nonlinear Dyn. 80(1–2), 715–721 (2015)

    Article  MathSciNet  Google Scholar 

  45. Su, C.Q., Gao, Y.T., Yu, X., Xue, L., Shen, Y.J.: Exterior differential expression of the \((1+1)\)-dimensional nonlinear evolution equation with Lax integrability. J. Math. Anal. Appl. 435(1), 735–745 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  46. Musette, M.: Painlevé Analysis for Nonlinear Partial Differential Equations. Springer, Berlin (1998)

    MATH  Google Scholar 

Download references

Acknowledgements

We express our sincere thanks to all the members of our discussion group for their valuable comments.

Author information

Authors and Affiliations

  1. School of Computer Information Management, Inner Mongolia University of Finance and Economics, Hohhot, 010070, China

    Zhong-Zhou Lan

  2. Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Jing-Jing Su

Authors
  1. Zhong-Zhou Lan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jing-Jing Su
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zhong-Zhou Lan or Jing-Jing Su.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work has been supported by the Science Research Project of Higher Education in Inner Mongolia Autonomous Region under Grant No. NJZZ18117, by the Natural Science Foundation of Inner Mongolia Autonomous Region under Grant No. 2018BS01004, by the China Postdoctoral Science Foundation under Grant No. 2018M640094, by the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region under Grant No. NJYT-19-B21, and by the National Natural Science Foundation of China under Grant No. 11772017.

Appendix

Appendix

For Mathematica code download please log in: https://github.com/ouyangyalin0312/Solitary-and-rogue-waves-solutions-for-NA-GAB-system.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lan, ZZ., Su, JJ. Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system. Nonlinear Dyn 96, 2535–2546 (2019). https://doi.org/10.1007/s11071-019-04939-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04939-1

Keywords

Search

Navigation