Skip to main content

Advertisement

SpringerLink
Log in

Investigation of coupled lever-bistable nonlinear energy harvesters for enhancement of inter-well dynamic response

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

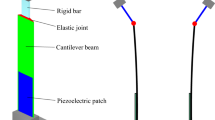
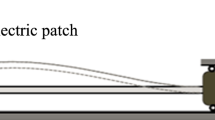
This paper proposes two new coupled lever-bistable nonlinear energy harvesters to enhance the inter-well dynamic response for improvement of vibration energy harvesting. For the first harvester, the oscillator mass and lever-supporting mass are on different sides of the lever pivot; for the second, both the masses are on the same side. The fundamental-periodic inter-well dynamics of both the lever-bistable energy harvesters are analytically, numerically and experimentally investigated in this study. Their variation trends are firstly studied analytically with respect to different lever parameters, which are also mathematically interpreted afterward. Subsequently, experiments are conducted to validate the theoretically predicted variation trends. The analytical and experimental results show that both the lever-bistable energy harvesters with appropriate lever parameters can significantly outperform the conventional bistable energy harvester. Finally, through numerical investigations, this paper reveals that different initial conditions of the lever-bistable energy harvesters can lead to other different types of inter-well responses apart from the fundamental-periodic responses, e.g., subharmonic response. The numerical results show that the fundamental-periodic inter-well response is more beneficial to energy harvesting than other inter-well responses. The basin-of-attraction map corresponding to each type of inter-well response is drawn to describe the distributions of each type’s initial condition. Based on the basin-of-attraction maps, both the lever-bistable energy harvesters’ occurring probabilities of exhibiting fundamental-periodic inter-well response are evaluated, which can quantitatively illustrate the lever structural benefit to stabilization of this favorable inter-well response.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  1. Daqaq, M.F.: On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 69, 1063–1079 (2012)

    Article  Google Scholar 

  2. Li, H., Qin, W., Zu, J., Yang, Z.: Modeling and experimental validation of a buckled compressive-mode piezoelectric energy harvester. Nonlinear Dyn. 92, 1761–1780 (2018)

    Article  Google Scholar 

  3. Yuan, T., Yang, J., Chen, L.Q.: Nonlinear characteristic of a circular composite plate energy harvester: experiments and simulations. Nonlinear Dyn. 90, 2495–2506 (2017)

    Article  Google Scholar 

  4. Liu, C., Jing, X.: Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia. Nonlinear Dyn. 88, 79–95 (2017)

    Article  Google Scholar 

  5. Stanton, S.C., McGehee, C.C., Mann, B.P.: Reversible hysteresis for broadband magnetopiezoelastic energy harvesting. Appl. Phys. Lett. 95, 174103 (2009)

    Article  Google Scholar 

  6. Daqaq, M.F., Masana, R., Erturk, A., Quinn, D.D.: On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion. Appl. Mech. Rev. 66, 040801 (2014)

    Article  Google Scholar 

  7. Tran, N., Ghayesh, M.H., Arjomandi, M.: Ambient vibration energy harvesters: a review on nonlinear techniques for performance enhancement. Int. J. Eng. Sci. 127, 162–185 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  8. Kovacic, I., Brennan, M.J.: The Duffing Equation: Nonlinear Oscillators and Their Behaviour. Wiley, Chichester (2011)

    Book  MATH  Google Scholar 

  9. Harne, R.L., Wang, K.W.: A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22, 023001 (2013)

    Article  Google Scholar 

  10. Harne, R.L., Wang, K.W.: Harnessing Bistable Structural Dynamics: For Vibration Control, Energy Harvesting and Sensing. Wiley, Chichester (2017)

    Book  MATH  Google Scholar 

  11. Cao, J., Zhou, S., Inman, D.J., Chen, Y.: Chaos in the fractionally damped broadband piezoelectric energy generator. Nonlinear Dyn. 80, 1705–1719 (2015)

    Article  Google Scholar 

  12. Ali, S.F., Adhikari, S., Friswell, M.I., Narayanan, S.: The analysis of piezomagnetoelastic energy harvesters under broadband random excitations. J. Appl. Phys. 109, 074904 (2011)

    Article  Google Scholar 

  13. Kumar, P., Narayanan, S., Adhikari, S., Friswell, M.I.: Fokker–Planck equation analysis of randomly excited nonlinear energy harvester. J. Sound Vib. 333, 2040–2053 (2014)

    Article  Google Scholar 

  14. Erturk, A., Inman, D.J.: Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 330, 2339–2353 (2011)

    Article  Google Scholar 

  15. Tang, L., Yang, Y., Soh, C.K.: Improving functionality of vibration energy harvesters using magnets. J. Intell. Mater. Syst. Struct. 23, 1433–1449 (2012)

    Article  Google Scholar 

  16. Stanton, S.C., McGehee, C.C., Mann, B.P.: Nonlinear dynamics for broadband energy harvesting: investigation of a bistable piezoelectric inertial generator. Physica D 239, 640–653 (2010)

    Article  MATH  Google Scholar 

  17. Lan, C., Tang, L., Qin, W., Xiong, L.: Magnetically coupled dual-beam energy harvester: benefit and trade-off. J. Intell. Mater. Syst. Struct. 29, 1216–1235 (2018)

    Article  Google Scholar 

  18. Gao, Y.J., Leng, Y.G., Fan, S.B., Lai, Z.H.: Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet. Smart Mater. Struct. 23, 095003 (2014)

    Article  Google Scholar 

  19. Masana, R., Daqaq, M.F.: Electromechanical modeling and nonlinear analysis of axially loaded energy harvesters. J. Vib. Acoust. 133, 011007 (2010)

    Article  Google Scholar 

  20. Zhang, J., Zhang, J., Shu, C., Fang, Z.: Enhanced piezoelectric wind energy harvesting based on a buckled beam. Appl. Phys. Lett. 110, 183903 (2017)

    Article  Google Scholar 

  21. Li, H., Qin, W.: Dynamics and coherence resonance of a laminated piezoelectric beam for energy harvesting. Nonlinear Dyn. 81, 1751–1757 (2015)

    Article  MathSciNet  Google Scholar 

  22. Harne, R.L., Thota, M., Wang, K.W.: Concise and high-fidelity predictive criteria for maximizing performance and robustness of bistable energy harvesters. Appl. Phys. Lett. 102, 053903 (2013)

    Article  Google Scholar 

  23. Jiang, W.A., Chen, L.Q.: Snap-through piezoelectric energy harvesting. J. Sound Vib. 333, 4314–4325 (2014)

    Article  Google Scholar 

  24. Harne, R.L., Wang, K.W.: Axial suspension compliance and compression for enhancing performance of a nonlinear vibration energy harvesting beam system. J. Vib. Acoust. 138, 011004 (2016)

    Article  Google Scholar 

  25. Nguyen, M.S., Yoon, Y.J., Kwon, O., Kim, P.: Lowering the potential barrier of a bistable energy harvester with mechanically rectified motion of an auxiliary magnet oscillator. Appl. Phys. Lett. 111, 253905 (2017)

    Article  Google Scholar 

  26. Chen, L.Q., Jiang, W.A.: Internal resonance energy harvesting. J. Appl. Mech. 82, 031004 (2015)

    Article  Google Scholar 

  27. Xiong, L., Tang, L., Mace, B.R.: A comprehensive study of 2: 1 internal-resonance-based piezoelectric vibration energy harvesting. Nonlinear Dyn. 91, 1817–1834 (2018)

    Article  Google Scholar 

  28. Wu, Z., Harne, R.L., Wang, K.W.: Energy harvester synthesis via coupled linear bistable system with multi stable dynamics. J. Appl. Mech. 81, 061005 (2014)

    Article  Google Scholar 

  29. Wu, H., Tang, L., Yang, Y., Soh, C.K.: Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 25, 1875–1889 (2014)

    Article  Google Scholar 

  30. Lan, C., Qin, W.: Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 85, 71–81 (2017)

    Article  Google Scholar 

  31. Zhou, S., Cao, J., Erturk, A., Lin, J.: Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 102, 173901 (2013)

    Article  Google Scholar 

  32. Zhou, S., Cao, J., Inman, D.J., Liu, S., Wang, W., Lin, J.: Impact-induced high-energy orbits of nonlinear energy harvesters. Appl. Phys. Lett. 106, 093901 (2015)

    Article  Google Scholar 

  33. Zheng, R., Nakano, K., Hu, H., Su, D., Cartmell, M.P.: An application of stochastic resonance for energy harvesting in a bistable vibrating system. J. Sound Vib. 333, 2568–2587 (2014)

    Article  Google Scholar 

  34. Yilmaz, C., Kikuchi, N.: Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications. J. Sound Vib. 291, 1004–1028 (2006)

    Article  Google Scholar 

  35. Wei, C., Jing, X.: Vibrational energy harvesting by exploring structural benefits and nonlinear characteristics. Commun. Nonlinear Sci. 48, 288–306 (2017)

    Article  MathSciNet  Google Scholar 

  36. Liang, J., Zhao, Y., Zhao, K.: Synchronized triple bias–flip interface circuit for piezoelectric energy harvesting enhancement. IEEE Trans. Power Electr. 34, 275–286 (2019)

    Article  Google Scholar 

  37. Erturk, A., Inman, D.J.: Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. 17, 065016 (2008)

    Article  Google Scholar 

  38. Stanton, S.C., Owens, B.A., Mann, B.P.: Harmonic balance analysis of the bistable piezoelectric inertial generator. J. Sound Vib. 331, 3617–3627 (2012)

    Article  Google Scholar 

  39. Yang, K., Harne, R.L., Wang, K.W., Huang, H.: Investigation of a bistable dual-stage vibration isolator under harmonic excitation. Smart Mater. Struct. 23, 045033 (2014)

    Article  Google Scholar 

  40. Udani, J.P., Arrieta, A.F.: Efficient potential well escape for bi-stable Duffing oscillators. Nonlinear Dyn. 92, 1045–1059 (2018)

    Article  Google Scholar 

  41. Lu, Z., Yang, T., Brennan, M.J., Liu, Z., Chen, L.Q.: Experimental investigation of a two-stage nonlinear vibration isolation systems with high-static-low-dynamic stiffness. J. Appl. Mech. 84, 021001 (2017)

    Article  Google Scholar 

  42. Lu, Z., Brennan, M.J., Chen, L.Q.: On the transmissibilities of a nonlinear vibration isolation system. J. Sound Vib. 375, 28–37 (2016)

    Article  Google Scholar 

  43. Harne, R.L., Wang, K.W.: On the fundamental and superharmonic effects in bistable energy harvesting. J. Intell. Mater. Syst. Struct. 25, 937–950 (2014)

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China (Grant Nos. 11802097, 51506063).

Author information

Authors and Affiliations

  1. School of Aerospace Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China

    Kai Yang & Fei Fei

  2. Department of Mechanical Engineering, McGill University, Montreal, QC, H3A 0C3, Canada

    Haichao An

Authors
  1. Kai Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fei Fei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haichao An
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kai Yang.

Ethics declarations

Conflict of interest

All authors declare that they have no conflict of interest.

Research involving human participants and/or animals

This work is about the mechanical engineering. This research does not involve any human participants or animals.

Informed consent

Only the authors listed in the manuscript are involved into this work. The submission of this research is agreed by all the authors listed in the manuscript and is permitted by both the affiliations of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, K., Fei, F. & An, H. Investigation of coupled lever-bistable nonlinear energy harvesters for enhancement of inter-well dynamic response. Nonlinear Dyn 96, 2369–2392 (2019). https://doi.org/10.1007/s11071-019-04929-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-04929-3

Keywords

Search

Navigation