Non-differentiability of quasi-potential and non-smooth dynamics of optimal paths in the stochastic Morris–Lecar model: Type I and II excitability

Abstract

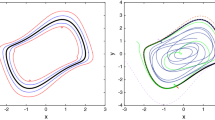
We studied the stochastic Morris–Lecar model of both Type I and II excitability using the large deviation theory. A mechanical interpretation for the discontinuity of the optimal path that has been found for decades in nearly all systems driven by weak white noise was provided. By doing that, we connected some long-separated concepts in mechanics, mathematics and physics: sliding set of non-smooth dynamical systems, non-differentiable set of the viscosity solution to the Hamilton–Jacobi equation and switch line, the singular structure which occurs in the Lagrangian manifold to characterize the sudden switch of optimal paths. We found that the existence of the sliding set engendered some novel dynamics in the case of Type I excitability. As for Type II, we found that the canard separatrix forms a boundary threshold of different dynamical behaviors and a crossing point in weak noise limit is located. Besides, the validity of this separatrix as the threshold is verified by a comparison with a level curve of quasi-potential at the cusp of the switching line.

Appendix

Parameters of the dimensionless Morris–Lecar model have been chosen according to Refs. [40, 41] as:

Type I Excitability: $I=0.05$, $\phi =0.2$, $V_k=-0.7$, $V_{Ca}=1$, $V_L=-0.5$, $g_l=0.5$, $g_k=2$, $g_{Ca}=1.33$, $V_1=-0.01$, $V_2=0.15$, $V_3=0.1$, $V_4=0.145$;

Type II Excitability: $I=0.05$, $\phi =0.2$, $V_k=-0.7$, $V_{Ca}=1$, $V_L=-0.5$, $g_l=0.5$, $g_k=2$, $g_{Ca}=1.33$, $V_1=-0.01$, $V_2=0.15$, $V_3=0.017$, $V_4=0.25$;